12. Формула Ньютона-Лейбница.

ПустьF(x) -произвольная первообразная для функции f(x), заданной на промежутке [a,b]. Так как две первообразные одной и той же функции отличаются на постоянное слагаемое, то верно равенство (1):

( в качестве числа х₀ взято число а).

Вэтом тождестве положим х=а и получим , Откуда С = -F(a). Заменяя здесь х на b, приходим к формуле Ньютона-Лейбница:

Если - первообразная непрерывной функции на , то:.

Док-во: Рассмотрим тождество

Преобразуем каждую разность в скобках по формуле Лагранжа

. Получим 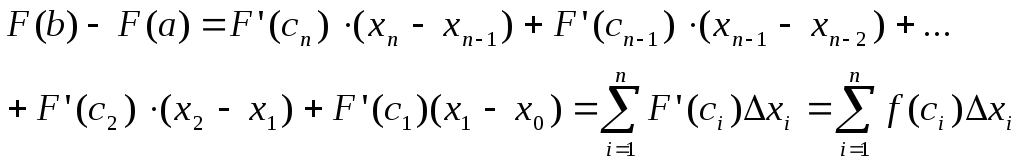т.е., гдеесть нек-рая точка интервала. Т.к. функцияy=f(x) непрерывна на [a;b]. Поэтому существует предел интегральной суммы, равный определенному интегралу от f(x) на [a;b].

Переходя к пределу при , получаемF(b)-F(a)=

=, т.е. .

интеграл с переменным верхним пределом

Если изменять, например, верхний предел так, чтобы не выйти за пределы отрезка [a;b], то величина интеграла будет изменяться. Другими словами, интеграл с переменным верхним пределом представляет собой функцию своего верхнего предела. Производная определенного интег-ла по переменному верхнему пределу равна подынтегральной функции, в к-рой переменная интегрирования заменена этим пределом, т.е.

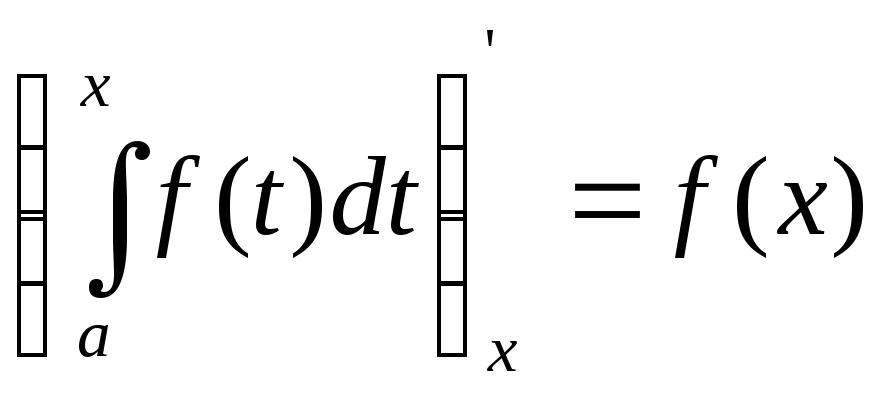Док-во: По формуле Ньютона-Лейбница имеем:.

Следовательно,

=.

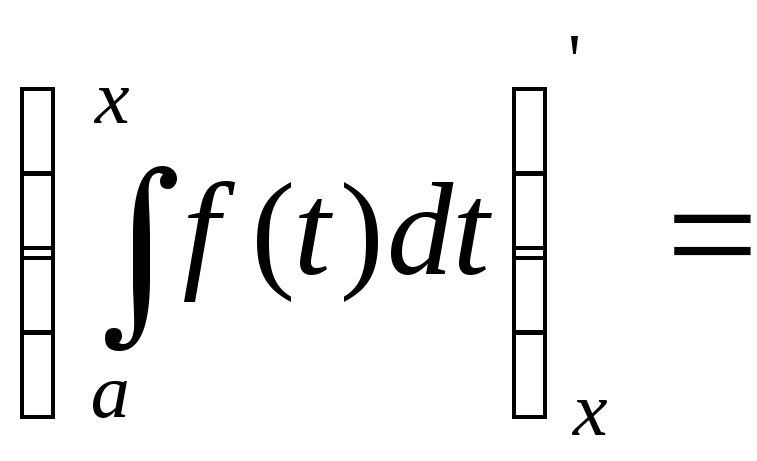
Это значит, что определенный интег-л с переменным верхним пределом есть одна из первообразных подынтегральной функции.

13. Замена переменной в определенном интеграле.

Теорема: при замене переменной х на t по формуле x=φ(t) равенство (1)

Справедливо при условиях:

1. φ(α) = а, φ(β) = b,

2. φ'(t) непрерывна на отрезке [α,β],

3 f(x) непрерывна на отрезке [a,b], а f[φ(t)] определена непрерывна на отрезке [α,β].

Доказательство: при наших предположениях левая и правая части равенства (1) существуют и существуют первообразные подынтегральные функции. Пусть ∫f(x)dx = F(x)+C. Тогда, как легко проверить дифференцированием обеих частей, справедливо равенство ∫f[φ(t)]φ'(t)dt = F[φ(t)]+C правая часть дифференцируется как сложная функция). Применяем формулу Ньютона-Лейбница

Получаем (по условию 1)

правые части этих двух равенств оказываются одинаковыми, следовательно, можно приравнять левые части. Приравнивая их, приходим к равенству(1).

Замена переменной в определенном интеграле.

Теорема: пусть f(x) – непрерывная функция на отрезке , функция х = (t) непрерывно дифференцируема на , () = а и () = b. Тогда справедлива формулаДоказательство: По формуле Ньютона-Лейбница где F(x) – какая-нибудь первообразная для функции f(x) на . Рассмотрим на отрезке сложную функцию от переменной t: Ф(t) = F((t)). Согласно правилу дифференцирования сложной функции находим:

Ф(t) = F((t))(t) = f((t))(t).Отсюда следует, что функция Ф(t) является первообразной для функции f((t))(t), непрерывной на . Поэтому, согласно формуле Ньютона-Лейбница получаем:

14.Формула прямоугольников

Если известны значения функции f(x) в некоторых точках x₀, x₁, … , x_m, то в качестве функции “близкой” к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.

Если разбить отрезок интегрирования на n равных частей . Приэтом:y₀ = f(x₀), y₁ = f(x₁), …. , y_n = f(x_n).

Составим суммы: y₀x + y₁x + … + y_n-1x

y₁x + y₂x + … + y_nx

Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной

Тогда

или

любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.

Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников

Формула трапеций.

Эта формула является более точной по сравнению с формулой прямоугольников.

Подинтегральная функция в этом случае заменяется на вписанную ломаную.

y₁ у₂ у_n

a x₁ x₂ b x

Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.

Площади вписанных трапеций вычисляются по формулам:

После приведения подобных слагаемых получаем формулу трапеций:

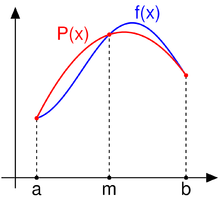
Формула Симпсона (также Ньютона-Симпсона[1]) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).

Суть приёма заключается в приближении подынтегральной функции на отрезке [a,b] интерполяционным многочленом второй степени p2(x), т.е. приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]: где f(a), f((a + b) / 2) и f(b) — значения функции в соответствующих точках (на концах отрезка и в его середине).