Тема 2. Краткие сведения из алгебры многочленов

1. Решение квадратных уравнений. Теорема Виета.

Теорема 1.2.Уравнение,иимеет два действительных корня, которые находятся по формулам.

Теорема 2.2(Теорема Виета). Если- корни уравнения (∗), то.

Следствие. Корни приведённого квадратного уравненияпри условиинаходятся по формулами теорема Виета для корней этого уравнения:.

Теорема 3.2.(Обратная теорема Виета). Если, то- корни квадратного уравнения.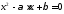

Следствие. Если- корни уравнения, то.

Пример 14.1) Найдите приведённое квадратное уравнение с корнями.

Так как , то по теореме, обратной теореме Виета,- корни приведённого квадратного уравнения.

2) При каких значениях параметра оба корня уравненияположительны?

Для существования действительных корней уравнения требуется выполнение условия . Итак,.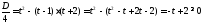

Числа одного знака, если, а оба положительны, если

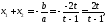
Но по теореме Виета . Поэтому оба корня уравнения (1) положительны, если

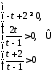
2. Решение уравнений третьей и четвёртой степени в радикалах.

Алгоритм решения уравнений третьей степени в радикалах.

1. Уравнение третьей степени делением обеих частей наприводим к равносильному уравнению.

2. Заменой приводим к уравнению.

3. Вычисляем - дискриминант кубического уравнения.

4. Находим один из корней уравнения 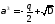, вообще говоря, с комплексными коэффициентами (если, то берём любой комплексный квадратный корень из), и число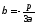. При этом, если, то и, и в пункте 2 уравнение принимает вид, решение которого очевидно.

5. Если , то находим корни уравнения:, где- комплексные недействительные корни кубические из единицы.

6. Находим корни исходного уравнения .

Теорема 4.2. (О множестве всех решений кубического уравнения с действительными коэффициентами). Пусть- дискриминант кубического уравнения (1). Тогда

1) если , то уравнение (1) имеет один действительный и два недействительных комплексных сопряжённых корня;

2) если , то все три корня уравнения (1) действительные и хотя бы два из них совпадают;

3) если , то все три корня уравнения (1) действительные и различные.

Пример 15.Решить уравнениеметодом Кардано.

Так как исходное уравнение является приведённым, то сразу делаем замену :.

Итак, . Тогда. Значит, по теореме 4.2 уравнение имеет один действительный и два недействительных комплексных сопряжённых корня. Находим один из корней уравненияили. Возьмём. Тогда. Поэтому,,.

Находим корни исходного уравнения по формулам: . Итак,.

Алгоритм решения уравнений четвёртой степени в радикалах.

1. Уравнение четвёртой степени делением обеих частей наприводим к равносильному уравнению.

2. Заменой приводим к уравнению (2).

3.Находим - один из корней кубического уравнения.

4. Все корни уравнения (2) находим, как корни совокупности уравнений

где - один из комплексных квадратных корней из комплексного числа, а- другой корень.

5. Находим корни исходного уравнения по формулам: .

Уравнения третьей и четвёртой степени в общем виде (т.е. с выводом формул, выражающих корни уравнения через его коэффициенты в радикалах) были решены в начале и середине 16 века итальянскими математиками дель Ферро, Никколо Тарталья, Джироламо Кардано и Луиджи Феррари. И только в начале 19 века норвежский математик Нильс Хенрик Абель, опираясь на труды многочисленных предшественников, в частности, Гаусса и Лагранжа, доказал, что невозможно корни уравнений пятой и выше степени выразить через коэффициенты соответствующего уравнения в радикалах. А полностью задачу о разрешимости уравнений в радикалах решил француз Эварист Галуа. И так как уравнения пятой и выше степени не имеют решения в общем виде, то пришлось искать другие приёмы их решения, вылившиеся в теорию многочленов.

3. Многочлены. Основные понятия и свойства. Делимость. Теорема Безу.

Определения и обозначения. Ненулевой многочлен с коэффициентами из некоторого полязаписывается в канонической форме (или в каноническом виде) как выражение, где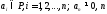- неотрицательное целое число. При этом числоназываетсястепенью многочлена .-старший коэффициент,- свободный член многочлена. Степенью нулевого многочленаназывается символ. Степень многочленаобозначается. Множество всех многочленов с коэффициентами из поляобозначается как.

Теорема 5.2.(О свойствах степени). Для любых многочленовс коэффициентами из полявыполняются свойства:

1)

2)

Определение.Многочленделитсяна многочлен, если существует многочлентакой, что.

Обозначение.⋮.

_{Пример 16.}1)⋮над любым числовым полем. 2)⋮над полем комплексных чисел. 3) Для любого натурального числаи элементавыполняются свойства:⋮, в частности,_{⋮; ⋮.}

Теорема 6.2.(Свойства делимости многочленов). Для любых многочленоввыполняются свойства:

1. ⋮0⋮и для любого:⋮.

2. Если ⋮и⋮, то⋮.

3. Если и⋮, то.

4. Если ⋮и⋮, то существует:.

5. Если ⋮то⋮.

6. Если ⋮и⋮, то⋮.

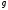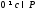Определение. Многочленыназываютсяассоциированныминад полем, если существуеттакой, что.

Обозначение.Ассоциированность над полеммногочленовобозначается как.

Следствия.1) Если, то множество всех многочленов, ассоциированных снад полем_,имеет вид:, где. 2)⋮и⋮.

Определение.Пустьи элемент. Тогда значением многочленаприназывается выражение (элемент поля).

Теорема 7.2. (Теорема Безу). Пусть. Тогда существует, причём единственный многочлентакой, что.

Определение. Элементназываетсякорнеммногочлена, если.

Следствие из теоремы Безу.Элементявляется корнем многочленатогда и только тогда, когда⋮.