
- •Содержание дисциплины
- •Тема 1. Краткие сведения из теории чисел
- •2. Наибольший общий делитель (нод). Алгоритм Евклида.
- •4.Взаимно простые числа. Наименьшее общее кратное (нок).
- •5. Простые и составные числа. Основная теорема арифметики.
- •7. Целые систематические числа.
- •8. Конечные и бесконечные десятичные дроби.
- •10. Решение уравненияв целых числах для целых чисел.
- •11. Признаки делимости.
- •Тема 2. Краткие сведения из алгебры многочленов
- •4. Деление с остатком в . Схема Горнера.
- •5. Наибольший общий делитель. Взаимная простота и неприводимость.
- •6. Многочлены над полем комплексных чисел .
- •7. Многочлены над полем действительных чисел.
- •8. Многочлены над полем рациональных чисел .
- •9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
- •10. Освобождение от алгебраической иррациональности в знаменателе.
- •11. Симметрические многочлены и их применение.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
Вариант 10
1. Решите уравнения в целых числах:
а)

б)

2. Найдите НОД(a,b) и линейно выразите его черезa иbс целыми коэффициентами, еслиa=1656,b=2232.
3. Докажите, что для любых целых чисел
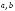 ,
если
,
если делится на 19, то и
делится на 19, то и делится на 19.
делится на 19.
4. Решите систему в натуральных числах:

5. Сложите дроби, приведя их к наименьшему
общему знаменателю:

6. Сформулируйте и докажите признак делимости на mв десятичной системе счисления. Будет ли числоаделится наm, еслиm=66,а=27544524?
7. Докажите, что следующие числа не
могут быть простыми одновременно:

8. Найдите все возможные цифры xиyтакие, что делится на 36.
делится на 36.
9. Докажите иррациональность
действительного числа
 ,
если
,
если
 .
.
10. Найдите все натуральные числа
 такие, что:
такие, что:
а)
 -
различные простые числа;
-
различные простые числа;
б)
 делится на 15 и
делится на 15 и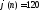 .
.
11. Переведите из одной системы счисления
в другую:
 в восьмеричную.
в восьмеричную.
12. Найдите остаток от деления
 на
на и выполните действия в указанной системе
счисления
и выполните действия в указанной системе
счисления .
.
13. Представьте следующие бесконечные десятичные дроби в виде обыкновенных несократимых дробей: а) 0,(624); б) 0,27(31).
14. Найдите каноническую форму записи натуральных чисел aиb, еслиa=4663,b=58867.
15. Укажите общую формулу целых чисел n,
для которых сократима дробь .
.
16. Найдите длину предпериода десятичной
дроби, в которую обращается обыкновенная
дробь
 .
.
17. Решите уравнения в целых числах а)
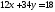 ;
б)
;
б)
18. Найдётся ли на прямой 3х-24у=19 хотя бы одна точка с целочисленными координатами?
19. Решите в целых числах уравнение x+y=xy.
20. Целое число nпри делении на 2 даёт остаток 1, при делении на 3 – остаток 2. Какой остаток даётnпри делении на 6?
21. Докажите, что произведение трёх последовательных целых чисел делится на 6.
22. Известно, что целое число 2n+1 - точный квадрат. Докажите, чтоnделится на 4 (n– целое число).
23. Найдите трёхзначное число, которое равно квадрату некоторого двузначного числа и кубу некоторого однозначного.
24. Найдите наименьшее натуральное число, которое после умножения на 2 станет квадратом, а после умножения на 3 – кубом некоторых натуральных чисел.
25. Найдите все простые числа pиqтакие, чтоp2-2q2=1.
26. Произведение числа 21 на некоторое натуральное четырёхзначное число – точный куб. Найдите это четырёхзначное число.
27. Докажите, что число, записанное тридцатью единицами и каким угодно количеством нулей, не является точным квадратом.
28. При каком условии
 делится на
делится на ?
?
29.Разделите
 на
на при а)
при а) и б)
и б) .
.
30. Вычислите
 ,
если
,
если и
и .
.
31. Многочлен  разложите по степеням
разложите по степеням .
.
32. Разложите на множители с целыми
коэффициентами многочлен
 .
.
33. При каких значениях параметра
 корни уравнения
корни уравнения положительны?
положительны?
34. Решите уравнение
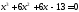 методом Кардано.
методом Кардано.
35. Освободитесь от алгебраической
иррациональности в знаменателе
 .
.
36. Найдите сумму кубов корней уравнения
 .
.
37. Решите уравнение
 .
.
38. Решите систему

39. Разложите на множители с целыми
коэффициентами

40. Найдите по алгоритму все рациональные
корни многочлена
 ,
если
,
если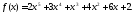
Вариант 11
1. Решите уравнения в целых числах:
а)

б)

2. Найдите НОД(a,b) и линейно выразите его черезa иbс целыми коэффициентами, еслиa=2525,b=3225.
3. Докажите, что для любых целых чисел
 ,
если
,
если делится на 23, то и
делится на 23, то и делится на 23.
делится на 23.
4. Решите систему в натуральных числах:

5. Сложите дроби, приведя их к наименьшему
общему знаменателю:

6. Сформулируйте и докажите признак делимости на mв десятичной системе счисления. Будет ли числоаделиться наm, еслиm=40,а=27544524?
7. Докажите, что следующие числа не
могут быть простыми одновременно:
8. Найдите все возможные цифры xиyтакие, что делится на 20.
делится на 20.
9. Докажите иррациональность
действительного числа
 ,
если
,
если .
.
10. Найдите все натуральные числа
 такие, что:
такие, что:
а)
 -
различные простые числа;
-
различные простые числа;
б)
 делится на 10 и
делится на 10 и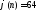 .
.
11. Переведите из одной системы счисления
в другую:
 в девятеричную.
в девятеричную.
12. Найдите остаток от деления
 на
на и выполните действия в указанной системе
счисления
и выполните действия в указанной системе
счисления .
.
13. Представьте следующие бесконечные десятичные дроби в виде обыкновенных несократимых дробей: а) 0,(37); б) 0,21(93).
14. Найдите каноническую форму записи натуральных чисел aиb, еслиa=5701,b=43993.
15. Укажите общую формулу целых чисел n,
для которых сократима дробь .
.
16. Найдите длину предпериода десятичной
дроби, в которую обращается обыкновенная
дробь
 .
.
17. Решите уравнения в целых числах а)
 ;
б)
;
б) .
.
18. Найдётся ли на прямой 7х-35у=18 хотя бы одна точка с целочисленными координатами?
19. Решите в целых числах уравнение x+y=xy.
20. Целое число nпри делении на 2 даёт остаток 1, при делении на 3 – остаток 2. Какой остаток даётnпри делении на 6?
21. Докажите, что произведение трёх последовательных целых чисел делится на 6.
22. Известно, что целое число 2n+1 - точный квадрат. Докажите, чтоnделится на 4 (n– целое число).
23. Найдите трёхзначное число, которое равно квадрату некоторого двузначного числа и кубу некоторого однозначного.
24. Найдите наименьшее натуральное число, которое после умножения на 2 станет квадратом, а после умножения на 3 – кубом некоторых натуральных чисел.
25. Найдите все простые числа p иqтакие, чтоp2-2q2=1.
26. Произведение числа 21 на некоторое натуральное четырёхзначное число – точный куб. Найдите это четырёхзначное число.
27. Докажите, что число, записанное тридцатью единицами и каким угодно количеством нулей, не является точным квадратом.
28. При каком условии
 делится на
делится на ?
?
29.Разделите
 на
на при а)
при а) и б)
и б) .
.
30. Вычислите
 ,
если
,
если и
и .
.
31. Многочлен
 разложите по степеням
разложите по степеням
 .
.
32. Разложите на множители с целыми
коэффициентами многочлен

33. При каких значениях параметра
 корни уравнения
корни уравнения положительны?
положительны?
34. Решите уравнение
 методом Кардано.
методом Кардано.
35. Освободитесь от алгебраической
иррациональности в знаменателе
 .
.
36. Найдите сумму кубов корней уравнения
 .
.
37. Решите уравнение
 .
.
38. Решите систему

39. Разложите на множители с целыми
коэффициентами

40. Найдите по алгоритму все рациональные
корни многочлена
 ,
если
,
если
