
- •Содержание дисциплины
- •Тема 1. Краткие сведения из теории чисел
- •2. Наибольший общий делитель (нод). Алгоритм Евклида.
- •4.Взаимно простые числа. Наименьшее общее кратное (нок).
- •5. Простые и составные числа. Основная теорема арифметики.
- •7. Целые систематические числа.
- •8. Конечные и бесконечные десятичные дроби.
- •10. Решение уравненияв целых числах для целых чисел.
- •11. Признаки делимости.
- •Тема 2. Краткие сведения из алгебры многочленов
- •4. Деление с остатком в . Схема Горнера.
- •5. Наибольший общий делитель. Взаимная простота и неприводимость.
- •6. Многочлены над полем комплексных чисел .
- •7. Многочлены над полем действительных чисел.
- •8. Многочлены над полем рациональных чисел .
- •9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
- •10. Освобождение от алгебраической иррациональности в знаменателе.
- •11. Симметрические многочлены и их применение.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
8. Конечные и бесконечные десятичные дроби.
Определение.Конечной –ичной
систематической дробью называется
число (
–ичной
систематической дробью называется
число ( )
) ,
где
,
где –целое
систематическое число,
–целое
систематическое число, -целые
числа такие, что
-целые
числа такие, что .
.
Для записи дроби
 ,
где
,
где - натуральные числа, в виде
- натуральные числа, в виде –ичной
систематической дроби, достаточно
научиться делать это для правильных
обыкновенных дробей. В этом случае
–ичной
систематической дроби, достаточно
научиться делать это для правильных
обыкновенных дробей. В этом случае и
и .
.
Теорема 14.1.Правильная несократимая
дробь может быть представлена в виде (
может быть представлена в виде ( )
тогда и только тогда, когда в разложение
знаменателя
)
тогда и только тогда, когда в разложение
знаменателя на простые множители входят только те
простые числа, которые входят и в
разложение на простые множители основания
на простые множители входят только те
простые числа, которые входят и в
разложение на простые множители основания .
.
Следствие.Несократимая дробь может быть представлена в виде конечной
десятичной дроби тогда и только тогда,
когда в разложение знаменателя
может быть представлена в виде конечной
десятичной дроби тогда и только тогда,
когда в разложение знаменателя на простые множители входят лишь числа
2 и 5, т.е.
на простые множители входят лишь числа
2 и 5, т.е. ,
где
,
где -
целые неотрицательные числа.
-
целые неотрицательные числа.
Пример 10.Представьте дробь в виде конечной двенадцатеричной
систематической дроби.
в виде конечной двенадцатеричной
систематической дроби.
Так как
 ,
а
,
а ,
то дробь
,
то дробь представима в требуемом виде. Тогда
представима в требуемом виде. Тогда Здесь
Здесь - максимальный из показателей чисел 2 и
3 в каноническом представлении числа
24 (знаменателя дроби). Но
- максимальный из показателей чисел 2 и
3 в каноническом представлении числа
24 (знаменателя дроби). Но .
Значит,
.
Значит,
 .
.
Аналогичный приём представления дроби
 в виде конечной систематической дроби
по любому основанию
в виде конечной систематической дроби
по любому основанию применим во всех случаях, когда знаменатель
дроби
применим во всех случаях, когда знаменатель
дроби удовлетворяет условию теоремы 14.1.
удовлетворяет условию теоремы 14.1.
Определение.Правильной бесконечной –ичной
дробью называется ряд (
–ичной
дробью называется ряд (
 )
) ,
где
,
где –целые
числа такие, что
–целые
числа такие, что для всех
для всех
Замечание.Так как для любого верно неравенство
верно неравенство ,
а ряд
,
а ряд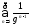 сходится как геометрическая прогрессия
со знаменателем
сходится как геометрическая прогрессия
со знаменателем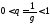 ,
то ряд (
,
то ряд ( )
сходится, т.е. существует единственное
действительное числоαтакое, что
)
сходится, т.е. существует единственное
действительное числоαтакое, что
Теорема 15.1.Если рациональное
число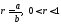 нельзя представить в виде конечной
нельзя представить в виде конечной -ичной
дроби (
-ичной
дроби ( ),
то число
),
то число единственным образом представляется
в виде правильной бесконечной
единственным образом представляется
в виде правильной бесконечной -ичной
дроби (
-ичной
дроби ( ).
).
Определение.Бесконечная правильная
систематическая дробь по основанию вида
вида называется чисто периодической с
периодом длины
называется чисто периодической с
периодом длины ,
если для всех натуральных
,
если для всех натуральных выполняется равенство
выполняется равенство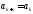 ,
причём
,
причём -
наименьшее натуральное число с таким
свойством (т.е. если
-
наименьшее натуральное число с таким
свойством (т.е. если ,
то обязательно найдётся натуральное
число
,
то обязательно найдётся натуральное
число такое, что
такое, что ).
).
Определение.Бесконечная правильная
систематическая дробь по основанию вида
вида называется смешанной периодической с
периодом длины
называется смешанной периодической с
периодом длины и предпериодом длины
и предпериодом длины ,
если для всех натуральных
,
если для всех натуральных выполняется равенство
выполняется равенство ,
причём
,
причём -
наименьшие натуральные числа с таким
свойством.
-
наименьшие натуральные числа с таким
свойством.
Обозначение. Чисто периодическую
дробь с периодом длины будем записывать в виде
будем записывать в виде ,
а смешанную периодическую дробь -
,
а смешанную периодическую дробь - .
.
Теорема 16.1.Если знаменатель
правильной несократимой дроби взаимно прост с основанием системы
счисления
взаимно прост с основанием системы
счисления ,
то дробь
,
то дробь представима в виде чисто периодической
представима в виде чисто периодической -ичной
дроби, период
-ичной
дроби, период которой является наименьшим натуральным
числом таким, что
которой является наименьшим натуральным
числом таким, что ⋮
⋮ .
.
Следствие.Правильная несократимая
дробь может быть представлена в виде чисто
периодической десятичной дроби тогда
и только тогда, когда
может быть представлена в виде чисто
периодической десятичной дроби тогда
и только тогда, когда .
При этом длина периода
.
При этом длина периода -
это наименьшее натуральное число такое,
что
-
это наименьшее натуральное число такое,
что ⋮
⋮ .
.
Теорема 17.1.Если -
каноническое представление числа
-
каноническое представление числа ,
причём
,
причём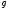 делится на
делится на ,
но не делится ни на одно из
,
но не делится ни на одно из ,
то правильная несократимая дробь
,
то правильная несократимая дробь может быть представлена в виде
может быть представлена в виде =
= -
смешанной периодической дроби, причём
длина предпериода
-
смешанной периодической дроби, причём
длина предпериода равна наибольшему из показателей
равна наибольшему из показателей (
( ,
а длина периода
,
а длина периода -наименьшее
натуральное число такое, что
-наименьшее
натуральное число такое, что ⋮
⋮ ,
где
,
где .
.
Пример 11.В виде каких десятичных
дробей представимы дроби 1) 2)
2)
3)

1) Так как
 ,
а 10=2∙5, то дробь
,
а 10=2∙5, то дробь представима в виде конечной десятичной
дроби:
представима в виде конечной десятичной
дроби:
2) Так как (10,17)=1, то дробь
 представима в виде чисто периодической
десятичной дроби. Прямым вычислением
находим, что
представима в виде чисто периодической
десятичной дроби. Прямым вычислением
находим, что не делится на 17 при всех натуральных
не делится на 17 при всех натуральных ,
а
,
а ⋮17.
Значит, длина периода
⋮17.
Значит, длина периода
3) Так как
 и 10⋮2; 5, но (10,17)=1,
то дробь
и 10⋮2; 5, но (10,17)=1,
то дробь представима в виде смешанной периодической
десятичной дроби с длиной периода
представима в виде смешанной периодической
десятичной дроби с длиной периода (предыдущее задание) и длиной предпериода
(предыдущее задание) и длиной предпериода
9. Решение уравнения (∗)
 в целых числах.
в целых числах.
Заметим, что из теоремы 11.1 легко следует,
что для любых целых чисел
 верны следующие утверждения. 1) Если
верны следующие утверждения. 1) Если ⋮
⋮ ,
то
,
то ⋮
⋮ .
2) Если
.
2) Если ,
, и
и ,
то
,
то - полные квадраты, т.е. такие числа, для
которых существуют целые числа
- полные квадраты, т.е. такие числа, для
которых существуют целые числа :
: .
.
Далее, если
 и
и -
целые решения уравнения (∗),
то
-
целые решения уравнения (∗),
то ⋮
⋮ .
Поэтому достаточно рассмотреть только
случай
.
Поэтому достаточно рассмотреть только
случай .
.
Более того, числа
 не могут быть оба нечётными. Действительно,
если
не могут быть оба нечётными. Действительно,
если ,
где
,
где ,
то
,
то
 Но тогда правая часть равенства, а
значит, и левая, делится на 2, но не делится
на 4. В этом случае сумма
Но тогда правая часть равенства, а
значит, и левая, делится на 2, но не делится
на 4. В этом случае сумма не может быть полным квадратом.
не может быть полным квадратом.
Рассмотрим случай, когда
 -
чётное целое число,
-
чётное целое число, -
нечётное (второй случай аналогичен
рассматриваемому). Тогда
-
нечётное (второй случай аналогичен
рассматриваемому). Тогда -
нечётное число и
-
нечётное число и ,
где оба множителя справа являются
нечётными целыми числами. Пусть
,
где оба множителя справа являются
нечётными целыми числами. Пусть .
Тогда
.
Тогда ,
где
,
где -
взаимно простые нечётные целые числа
и, выражая
-
взаимно простые нечётные целые числа
и, выражая из предыдущих равенств, получим:
из предыдущих равенств, получим: .
Кроме того,
.
Кроме того, ,
а значит,
,
а значит, ⋮
⋮ ,
, ⋮
⋮ ,
что по условиям выше влечёт равенство
,
что по условиям выше влечёт равенство .
Поэтому
.
Поэтому .
Но тогда
.
Но тогда -
полные квадраты,
-
полные квадраты,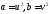 ,
где по предыдущему
,
где по предыдущему -
нечётные взаимно простые целые числа.
Таким образом, все определяющие (взаимно
простые) целые решения уравнения
-
нечётные взаимно простые целые числа.
Таким образом, все определяющие (взаимно
простые) целые решения уравнения имеют вид:
имеют вид: ,
где
,
где – нечётные взаимно простые целые числа.
– нечётные взаимно простые целые числа.
