
- •Содержание дисциплины
- •Тема 1. Краткие сведения из теории чисел
- •2. Наибольший общий делитель (нод). Алгоритм Евклида.
- •4.Взаимно простые числа. Наименьшее общее кратное (нок).
- •5. Простые и составные числа. Основная теорема арифметики.
- •7. Целые систематические числа.
- •8. Конечные и бесконечные десятичные дроби.
- •10. Решение уравненияв целых числах для целых чисел.
- •11. Признаки делимости.
- •Тема 2. Краткие сведения из алгебры многочленов
- •4. Деление с остатком в . Схема Горнера.
- •5. Наибольший общий делитель. Взаимная простота и неприводимость.
- •6. Многочлены над полем комплексных чисел .
- •7. Многочлены над полем действительных чисел.
- •8. Многочлены над полем рациональных чисел .
- •9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
- •10. Освобождение от алгебраической иррациональности в знаменателе.
- •11. Симметрические многочлены и их применение.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
10. Освобождение от алгебраической иррациональности в знаменателе.
Определение.Элемент называетсяалгебраическим над полем
называетсяалгебраическим над полем
 ,если
,если является корнем какого-нибудь ненулевого
многочлена с коэффициентами из поля
является корнем какого-нибудь ненулевого
многочлена с коэффициентами из поля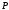 .
Если при этом
.
Если при этом ,
то
,
то -алгебраический иррациональный над
полем
-алгебраический иррациональный над
полем
 .
.
Пример 22.1) Любой элемент из поля
из поля является алгебраическим над
является алгебраическим над ,
т.к. является корнем ненулевого многочлена
,
т.к. является корнем ненулевого многочлена .
2) Элемент
.
2) Элемент является алгебраическим над полем
является алгебраическим над полем ,
т.к.
,
т.к. является корнем ненулевого многочлена
является корнем ненулевого многочлена .
3) Найдём ненулевой многочлен
.
3) Найдём ненулевой многочлен ,
корнем которого является элемент
,
корнем которого является элемент .
.
Найдём равенство, в котором линейная
комбинация целых неотрицательных
степеней
 равна 0.
равна 0.
Имеем



 .
Таким образом,
.
Таким образом, является корнем ненулевого многочлена
является корнем ненулевого многочлена .
Тем самым, дополнительно доказано, что
элемент
.
Тем самым, дополнительно доказано, что
элемент является алгебраическим над полем
является алгебраическим над полем .
.
Пусть
 - алгебраический иррациональный элемент
над полем
- алгебраический иррациональный элемент
над полем ;
;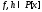 и
и .
Требуется элемент
.
Требуется элемент представить в виде линейной комбинации
неотрицательных степеней
представить в виде линейной комбинации
неотрицательных степеней с коэффициентами из поля
с коэффициентами из поля ,
т.е. исключить элемент
,
т.е. исключить элемент из знаменателя дроби. Достаточно
научиться решать данную задачу для
выражения
из знаменателя дроби. Достаточно
научиться решать данную задачу для
выражения .
.
Ищем многочлен
 такой, что
такой, что .
и
.
и .
Достаточно найти произвольный многочлен
.
Достаточно найти произвольный многочлен такой, что
такой, что .
Тогда можно взять многочлен
.
Тогда можно взять многочлен .
.
Поскольку
 ,
то существуют многочлены
,
то существуют многочлены :
: .
Но
.
Но .
Тогда из равенства
.
Тогда из равенства получаем
получаем ,
что и требуется.
,
что и требуется.
Пример 23.Освободиться от алгебраической
над полем иррациональности в выражении
иррациональности в выражении .
.
В данной задаче можно взять
 .
Или
.
Или .
Но мы возьмём
.
Но мы возьмём .
Тогда
.
Тогда и
и .
Ищем многочлен из
.
Ищем многочлен из ,
корнем которого является
,
корнем которого является :
:
 .
Возьмём многочлен
.
Возьмём многочлен .
Так как
.
Так как ,
то
,
то .
Найдём нужные многочлены
.
Найдём нужные многочлены .
Для этого делим
.
Для этого делим на
на (можно по схеме Горнера):
(можно по схеме Горнера):
|
|
1 |
0 |
-4 |
-32 |
-28 |
|
1 |
1 |
1 |
-3 |
-35 |
-63 |
Значит,
 .
Тогда
.
Тогда или
или .
Поэтому
.
Поэтому
Продолжая вычисления дальше, получим:

 .
.
11. Симметрические многочлены и их применение.
Определение.Степеньюодночлена от
от переменных
переменных называется число
называется число .Степеньюмногочлена от
.Степеньюмногочлена от переменных называется максимальная из
степеней его одночленов после приведения
подобных.
переменных называется максимальная из
степеней его одночленов после приведения
подобных.
Однородныммногочленом степени от
от переменных называется многочлен, у
которого все одночлены имеют одинаковую
степень
переменных называется многочлен, у
которого все одночлены имеют одинаковую
степень .
.
Понятие степени для многочленов от нескольких переменных играет вспомогательную роль. Основная роль отводится понятию лексикографического порядка.
Определение. Пусть - ненулевые одночлены от
- ненулевые одночлены от переменных
переменных :
:


 .
.
Положим
 старше
старше по лексикографическому порядку, если
существует
по лексикографическому порядку, если
существует такое, что
такое, что .
.
Определение.Старшим членоммногочлена от переменных называется старший по
лексикографическому порядку (после
приведения подобных).
переменных называется старший по
лексикографическому порядку (после
приведения подобных).
Замечание.Старший член произведения
двух ненулевых многочленов от переменных равен произведению их старших
членов.
переменных равен произведению их старших
членов.
Симметрические многочлены.
Определение.Многочлен от переменных
переменных называетсясимметрическим многочленом,если он не меняется при любой перестановке
его переменных
называетсясимметрическим многочленом,если он не меняется при любой перестановке
его переменных .
.
Замечание. Многочлен от переменных
переменных является симметрическим, если он не
меняется при перестановке его двух
любых переменных. Многочлен
является симметрическим, если он не
меняется при перестановке его двух
любых переменных. Многочлен является симметрическим от переменных
является симметрическим от переменных ,
но не является симметрическим от
,
но не является симметрическим от .
.
Определение.Элементарными
симметрическимимногочленами от переменных
переменных называются многочлены
называются многочлены

Легко видеть, что элементарные симметрические многочлены представляют из себя выражения в левых частях формул Виета.
Теорема 21.2.(О старшем члене симметрического многочлена).
1) Если
 - старший член симметрического многочлена
- старший член симметрического многочлена ,
то выполняется условие
,
то выполняется условие .
.
2) Для любого одночлена
 с условием (*) существует симметрический
многочлен вида
с условием (*) существует симметрический
многочлен вида со старшим членом, равным
со старшим членом, равным .
Причём
.
Причём .
.
Теорема 22.2.(Основная теорема о
симметрических многочленах). Каждый
симметрический многочлен от
от переменных может быть представлен как
многочлен от элементарных симметрических
многочленов
переменных может быть представлен как
многочлен от элементарных симметрических
многочленов ,
причём единственным образом с точностью
до перестановки слагаемых.
,
причём единственным образом с точностью
до перестановки слагаемых.
Алгоритм выражения симметрических многочленов через элементарные.
1) Пусть однородный симметрический многочлен.
однородный симметрический многочлен.
1. Приводим все подобные и находим старший
член
 по лексикографическому порядку:
по лексикографическому порядку: .
.
2. Выписываем набор показателей степеней
при переменных
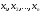 одночлена
одночлена
 и все возможные наборы неотрицательных
целых чисел
и все возможные наборы неотрицательных
целых чисел такие, что
такие, что .
.
3. Для каждого выписанного набора
показателей
 строим одночлен от
строим одночлен от вида
вида .
.
4. Берём сумму полученных одночленов,
взятых ровно по одному разу, причём
слагаемое, соответствующее набору для
 ,
берём с коэффициентом
,
берём с коэффициентом ,
а все остальные с неопределёнными
коэффициентами
,
а все остальные с неопределёнными
коэффициентами .
Приравниваем полученную сумму к
многочлену
.
Приравниваем полученную сумму к
многочлену :
:

5. Находим неопределённые коэффициенты
 .
Для этого задаём конкретные значения
переменным
.
Для этого задаём конкретные значения
переменным ,
находим для них значения элементарных
симметрических многочленов
,
находим для них значения элементарных
симметрических многочленов и
и ,
подставляем в равенство (*). Получим
соотношение для неопределённых
коэффициентов. Если требуется, задаём
ещё значения переменных и т.д.
,
подставляем в равенство (*). Получим
соотношение для неопределённых
коэффициентов. Если требуется, задаём
ещё значения переменных и т.д.
6. В равенство (*) подставляем найденные
значения неопределённых коэффициентов
и получаем выражение
 через элементарные симметрические
многочлены.
через элементарные симметрические
многочлены.
2)Неоднородный симметрический
многочлен разбиваем предварительно в
сумму однородных симметрических: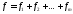 ,
каждый из которых представляем в виде
многочлена от элементарных симметрических
по предыдущему алгоритму:
,
каждый из которых представляем в виде
многочлена от элементарных симметрических
по предыдущему алгоритму: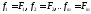 .
Сумма всех представлений и есть
представление данного симметрического
неоднородного многочлена в виде
многочлена от элементарных симметрических:
.
Сумма всех представлений и есть
представление данного симметрического
неоднородного многочлена в виде
многочлена от элементарных симметрических: .
.
Пример 24.Выразить симметрический
многочлен через элементарные симметрические
многочлены.
через элементарные симметрические
многочлены.
Находим старший по лексикографическому
порядку:
 ,
т.к. у него набор показателей (4;0;0), а у
остальных (0;4;0) и (0;0;4).
,
т.к. у него набор показателей (4;0;0), а у
остальных (0;4;0) и (0;0;4).
Выписываем набор показателей для старшего по лексикографическому порядку (4;0;0) и строим все возможные наборы с требуемыми в (*) условиями: (3;1;0), (2;2;0), (2;1;1). Других наборов нет.
Для каждого полученного набора строим
соответствующий одночлен от
 с положенными коэффициентами, берём их
сумму и приравниваем к
с положенными коэффициентами, берём их
сумму и приравниваем к :
:
 .
.
Находим неопределённые коэффициенты
 .
.
Эту задачу решаем, заполняя таблицу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом подбираем самые рациональные
наборы значений
 .
Например, если возьмём такой набор
значений, что
.
Например, если возьмём такой набор
значений, что ,
то из полученного одного уравнения
сразу найдём коэффициент
,
то из полученного одного уравнения
сразу найдём коэффициент .Такой
набор дан в первой строке таблицы:
.Такой
набор дан в первой строке таблицы:
|
|
|
|
|
|
|
|
|
|
1 |
1 |
-2 |
0 |
-3 |
-2 |
18 |
|
|
1 |
1 |
0 |
2 |
1 |
0 |
2 |
|
|
1 |
1 |
1 |
3 |
3 |
1 |
3 |
|
По набору значений
 в первой строке получаем:
в первой строке получаем: .
. .
Значит,
.
Значит, и
и .
.
Возьмём такой набор значений
 ,
чтобы
,
чтобы (вторая строка таблицы). Получим уравнение
(вторая строка таблицы). Получим уравнение .
Тогда
.
Тогда .
Теперь берём такой набор значений, чтобы
.
Теперь берём такой набор значений, чтобы (третья строка таблицы). Тогда получим
уравнение
(третья строка таблицы). Тогда получим
уравнение .
Поэтому
.
Поэтому .
Значит,
.
Значит, .
.
Пример 25.Решите уравнение .
.
Решаем, используя теорию симметрических
многочленов. Обозначим
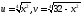 .
Тогда, складывая эти два равенства, а
затем складывая их четвёртые степени
(исключая
.
Тогда, складывая эти два равенства, а
затем складывая их четвёртые степени
(исключая из равенства), получаем систему
соотношений:
из равенства), получаем систему
соотношений: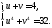
Выразим симметрический многочлен
 через элементарные симметрические
многочлены от двух переменных
через элементарные симметрические
многочлены от двух переменных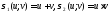 .
Заметим, что в данном случае это можно
сделать без использования основного
алгоритма. Действительно,
.
Заметим, что в данном случае это можно
сделать без использования основного
алгоритма. Действительно,
 .
Поэтому, полученная выше система
перепишется в виде
.
Поэтому, полученная выше система
перепишется в виде
Решаем полученную систему относительно
 .
Подставляя значение
.
Подставляя значение во второе уравнение системы, получим
во второе уравнение системы, получим или
или .
Тогда
.
Тогда или
или Таким образом, учитывая определение
Таким образом, учитывая определение ,
получим
,
получим или
или
По теореме, обратной теореме Виета,
 - корни квадратного уравнения
- корни квадратного уравнения в первом случае и
в первом случае и во втором.
во втором.
В первом случае получаем единственное
решение
 ,
а во втором
,
а во втором ,
действительных решений нет.
,
действительных решений нет.
Итак,
 или
или .
.
Пример 26.Решите уравнение .
.
Как и в предыдущем примере обозначим
 .
Тогда получаем систему
.
Тогда получаем систему Так как
Так как ,
а
,
а ,
то система преобразуется к виду:
,
то система преобразуется к виду:
Подставляя во второе уравнение выражение
 ,
получим квадратное уравнение
,
получим квадратное уравнение .
Решая его и вычисляя значения
.
Решая его и вычисляя значения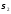 ,
сводим решение уравнения к решению
систем
,
сводим решение уравнения к решению
систем или
или
Подставим вместо
 их выражения:
их выражения:
 или
или
Как и в предыдущем примере по теореме,
обратной теореме Виета,
 корни соответствующих квадратных
уравнений
корни соответствующих квадратных
уравнений В первом случае
В первом случае и действительных корней нет. Во втором
случае
и действительных корней нет. Во втором
случае В силу симметричности вхождения
переменных
В силу симметричности вхождения
переменных получаем, что
получаем, что или
или
Из обозначений следует, что
 или
или
Пример 27. Решите уравнение
 в рациональных числах.
в рациональных числах.
Обозначим
 .
Тогда уравнение равносильно системе
.
Тогда уравнение равносильно системе
Возведём первые два слагаемые в квадрат
и сложим, а в левой части второго выполним
действия и получим систему относительно
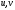 :
:

Левая часть второго уравнения не является
симметрическим многочленом относительно
 ,
но является симметрическим выражением.
,
но является симметрическим выражением.
Заметим, что
 и
и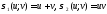 .
Тогда система преобразуется к виду
.
Тогда система преобразуется к виду
Имеем
 .
Подставляем в первое уравнение:
.
Подставляем в первое уравнение: .
.
Решаем это квадратное уравнение:
 или
или .
.
Поэтому
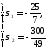 или
или Тогда по теореме, обратной теореме
Виета,
Тогда по теореме, обратной теореме
Виета, корни квадратных уравнений
корни квадратных уравнений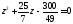 или
или В результате получим
В результате получим
Отбирая только рациональные решения и
учитывая симметричность вхождения
переменных
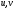 ,
получим:
,
получим: или
или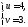 Так как
Так как ,
то
,
то
Пример 27.Решите систему уравнений
Обозначив
 ,
получим симметрическую систему
,
получим симметрическую систему
Учитывая, что
 ,
выражаем левые части обоих уравнений
через элементарные симметрические
,
выражаем левые части обоих уравнений
через элементарные симметрические :
: Откуда,
Откуда, или
или По теореме, обратной теореме Виета,
По теореме, обратной теореме Виета, - корни квадратного уравнения
- корни квадратного уравнения Получаем, что
Получаем, что
В силу симметричности вхождения
переменных
 ,
, или
или
А так как
 то окончательно получаем
то окончательно получаем
Таким образом, система имеет ровно два
решения
 или
или
Пример 28. Решите систему уравнений
Так как левые части уравнений являются
симметрическими многочленами, то
применяем теорию симметрических
многочленов. Выразим левые части
уравнений через элементарные симметрические
многочлены от двух переменных

Именно,
 ,
, .
.
Тогда изначальная система при введённых
обозначениях равносильна системе:

Подставляя значение
 во второе уравнение, получим уравнение
во второе уравнение, получим уравнение ,
одним из корней которого является -1.
Тогда уравнение представляется в виде
,
одним из корней которого является -1.
Тогда уравнение представляется в виде .
Многочлен
.
Многочлен не имеет действительных корней. Поэтому
система (*) имеет единственное действительное
решение
не имеет действительных корней. Поэтому
система (*) имеет единственное действительное
решение
Тогда
 и по теореме, обратной теореме Виета,
и по теореме, обратной теореме Виета, - корни квадратного уравнения
- корни квадратного уравнения Получаем
Получаем В силу симметричности вхождения
неизвестных
В силу симметричности вхождения
неизвестных ,
исходное уравнение имеет два решения:
,
исходное уравнение имеет два решения: или
или
Пример 29.Разложить на множители
многочлен .
.
Очень часто симметрические выражения легче разложить на множители, если представить их в виде выражений от элементарных симметрических многочленов.
Представим
 в виде многочлена от элементарных
симметрических многочленов
в виде многочлена от элементарных
симметрических многочленов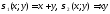 по известному алгоритму.
по известному алгоритму.
Находим старший по лексикографическому
порядку:
 .
Комбинация его показателей
.
Комбинация его показателей .
Теперь выписываем все возможные
комбинации показателей, удовлетворяющих
соответствующим условиям:
.
Теперь выписываем все возможные
комбинации показателей, удовлетворяющих
соответствующим условиям: .
Таким образом,
.
Таким образом, .
.
Ищем неопределённые коэффициенты
 :
:
|
|
|
|
|
|
|
|
1 |
-1 |
0 |
-1 |
-4 |
|
|
1 |
1 |
2 |
1 |
12 |
|
Итак, при
 получаем, что
получаем, что .
Тогда
.
Тогда
Если
 то получаем, что
то получаем, что ,
, ,
, .
Значит,
.
Значит,
 .
.
Итак,

Теперь, зная полученное разложение, можно придумать школьные способы для его получения.



























