
1.Папин А.А. Теоретическая механика
.pdfАлтайский государственный университет Математический факультет
Кафедра дифференциальных уравнений
А. А. Папин
Теоретическая механика
(краткий курс лекций)
Барнаул 2000
ВВЕДЕНИЕ
Теоретическая механика, являясь составной частью естествознания, изучает простейшую форму движения материи - механическое движение, которое заключается в изменении положения материального тела по отношению к другим телам с течением времени. Все движения материальных тел происходят в пространстве и во времени. В классической механике (И. Ньютон, "Математические принципы натуральной философии", 1687 год) постулируется, что
1.Пространство является трехмерным пространством Евклида с соответствующими определениями и понятиями. Метрические свойства пространства не зависят от наполняющей и движущейся в этом пространстве материи. Пространство однородно и изотропно, то есть его свойства одинаковы во всех точках и все направления в нем равноправны.
2.Время абсолютно для всех точек пространства. Его течение полагается однородным, непрерывным и не зависит от движущейся материи.
Принимая такие определения пространства и времени, отказываемся от рассмотрения эффектов механики теории относительности, в которой, на основе постоянства скорости света во всех инерциальных системах отсчета, устанавливается взаимосвязь пространства, времени и движущейся материи. Эффекты теории относительности становятся существенными при скоростях, близких к скоростям света. В классической механике скорости намного меньше скорости света.
При изучении механического движения рассматривается только два важнейших признака движущейся материи:
а) протяженность (геометрическая форма материального тела), б) вещественность (масса и ее распределение в данном объеме).
В рамках теоретической механики не рассматривается молекулярное строение вещества, то есть принимается предположение о непроницаемости вещества, что исключает возможность нахождения различных тел в одной и той же части пространства. Более того, объектом теоретической механики является не движение реальной материи, обладающей континуумом различных свойств, а некоторые абстрактные модели реальных тел, в том числе:
1.Материальная точка - модель, имеющая массу и не имеющая размеров
2.Абсолютно твердое тело - объем, сплошь заполненный веществом, причем расстояния между двумя любыми точками среды не изменяются во время движения.
3.Сплошная деформируемая среда - объем, заполненный веществом, причем расстояния между точками не обязаны сохраняться.
Эти основные модели могут объединяться в системы: системы свободных точек, системы со
связями, абсолютно твердое тело с полостью, заполненной жидкостью и т.д.
Для определения положения тела в пространстве необходимо, очевидно, иметь некоторое тело, по отношению к которому и определяется положение данного тела. Связанная с выбранным телом система координат (как правило - правая система декартовых координат) называется системой отсчета. Поскольку выбор системы отсчета в известной степени произволен, то понятия о механическом движении и равновесии являются относительными, то есть движущееся в одной системе тело, в другой может покоиться. Если же система отсчета не задана, то задача изучения движения тела становится неопределенной.
В механике важную роль играют инерциальные системы отсчета (собственное движение таких систем не может быть обнаружено никакими механическими опытами). Законы механики таковы, что предположение о существовании одной инерциальной системы приводит к существованию бесконечного числа таких систем. Все системы, движущиеся относительно исходной прямолинейно, равномерно и без вращения будут инерциальными.
Для описания механического взаимодействия тел вводится понятие о силе. Под механическим взаимодействием понимается такое действие тел друг на друга, в результате которого происходит или изменение движения этих тел, или изменение взаимного положения частей тел (деформация). Мерой механического взаимодействия является сила. Для данного тела сила является внешним фактором, изменяющим движение. Кроме этого внешнего фактора характер движения зависит от "степени податливости" тела оказываемому на него внешнему воздействию, или, как говорят степени инертности тела. Чем больше инертность тела, тем
медленнее изменяется его движение под действием данной силы и, наоборот. Мерой инертности материального тела является масса.
Как и в любой естественной дисциплине, основой теоретической механики является опыт и наблюдение (эксперимент), а свои результаты она соотносит с практикой.
Традиционно теоретическую механику делят на три составные части: кинематику, статику, динамику.
В кинематике движение изучается без учета причин, вызывающих последнее (то есть изучаются кинематические характеристики: уравнение движения, скорость, ускорение, геометрические свойства объекта). В статике изучается равновесие совокупности тел относительно некоторой системы отсчета. В динамике изучают движение под действием сил. Иногда статику и динамику объединяют в один раздел - кинетику.
Законы и аксиомы теоретической механики были сформулированы в результате трудов многих поколений ученых. Первые закономерности механики были получены в древнем Египте и Греции на основании опыта использования простейших механизмов и машин. Первая попытка изложить замкнутый круг идей, включающий известные тогда факты, была предпринята Аристотелем (384 - 322 г.г. до н.э.). Испытывая недостаток в экспериментальных фактах, Аристотель привлекал умозрительные гипотезы, что привело к неверным выводам (скорость падающих тел пропорциональна их весу; под действием постоянной силы тело движется с постоянной скоростью и т.п). Первые существенные результаты в области механики содержатся в работах Архимеда (287 - 212 г.г. до н.э.): закон гидростатики, работы по теории рычага, центр тяжести тел. Во II веке н.э. Птолемей сформулировал геоцентрическую картину мира. Интенсивное развитие естественных наук начинается в эпоху Возрождения. Кратко перечислим основные достижения в области механики в этот период. Леонардо да Винчи (1452 - 1519) - теория механизмов, трение в машинах, движение по наклонной плоскости. Коперник (1473 - 1543) - гелиоцентрическая картина мира. Кеплер (1571 - 1630) - благодаря работам Коперника и Тихо Браге, сформулировал три закона движения планет, послуживших Ньютону основанием его закона всемирного тяготения. Галилей (1564 - 1642) - закон инерции, свободное падение тел, движение тел, брошенных под углом к горизонту, прочность сооружений. Гюйгенс (1629 - 1695) - теория колебания математического маятника, понятие о моменте инерции твердого тела относительно оси. Ньютон завершил построение основ классической механики. Ему принадлежат закон действия и противодействия, закон всемирного тяготения. Основной закон механики (второй закон Ньютона) был впервые сформулирован в дифференциальной форме, что дало возможность рассмотреть многочисленные задачи. Известна также роль Ньютона (совместно с Лейбницем) в развитии анализа бесконечно малых. Эйлер (1707 - 1783), используя дифференциальное исчисление, рассмотрел задачи о движении несвободной точки, твердого тела, о течении идеальной жидкости, дал расчеты баллистических траекторий в сопротивляющейся среде. Даламбер (1717 - 1783) сформулировал вариационный принцип механики (в форме уравнений статики). Лагранж (1738 - 1813) открыл метод виртуальных перемещений и на его основе изложил основные результаты механики. Дальнейшее развитие теоретической механики связано с работами Лапласа, Гаусса, Гамильтона, Кирхгоффа, Гельмгольца, Герца, Остроградского, Ковалевской, Чебышева, Ляпунова, Жуковского, Мещерского, Циолковского, Четаева и многих других ученых.

Глава I. Кинематика.
Лекция 1. Вспомогательные сведения: векторные функции скалярного аргумента. Координатный, векторный, естественный способы описания движения точки. Кинематические характеристики: скорость, ускорение
Современная механика основывается на ряде закономерностей, установленных в форме, независимой от выбора системы координат, применяемых при получении и исследовании упомянутых закономерностях. Такая форма называется инвариантной. Математическим аппаратом, позволяющим находить основные соотношения механики в инвариантной форме, является тензорное исчисление [6]. Предполагается, что читателю известны основные свойства тензоров. Приведем для справки лишь некоторые, используемые в дальнейшем, сведения.
1. Вспомогательные сведения.
Рассмотрим правую декартовую систему координат Ox1 x2 x3 с соответствующими ортами kr1 , kr2 , kr3 . Для любых векторов ar = (a1 , a2 , a3 ) , b = (b1 ,b2 ,b3 ) определено скалярное
r |
r |
3 |
|
r |
|
|
r |
|
|
|
r r |
|
|
|
|
|||
a |
b = ∑aibi = |
a |
b |
cos(a,b) , |
|
(1.1.1) |
||||||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и векторное произведение |
|
|
|
|
|
|
|
|||||||||||
r |
r |
|
|
kr1 |
kr2 |
kr3 |
|
|
|
r |
r |
|
r |
|
r |
r r |
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
×b |
= |
|
a1 |
a2 |
a3 |
|
, |
|
a |
×b |
= |
a |
|
b |
sin(a,b) , |
(1.1.2) |
|
|
Здесь |
|
b1 |
b2 |
b3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
и далее принимается, что вектор ar×b ортогонален плоскости, проходящей |
||||||||||||||||
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
через вектора a |
и b , а его направление выбирается таким образом, чтобы из конца |
|||||||||||||||||
полученного вектора вращением первого из сомножителей для кратчайшего совмещения со вторым было видно происходящим против хода часовой стрелки.
r |
|
3 |
2 |
r r |
ar b |
|
|
||||
Здесь a |
= |
∑aα |
, cos(a,b) = |
r |
|
|
r |
|
, |
(1.1.3) |
|
|
|
||||||||||
|
|
α=1 |
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя свойства базисных векторов
krα ×krβ = δαβ
kr1 ×kr2 = kr3 , k1 ×k1 = 0 ,
0, α ≠ β |
|
||
= |
|
|
|
1,α = β |
|
||
r |
r |
r |
k3 ×k1 = k2 , |
k2 |
×k3 |
= k1 , |
|
k2 ×k2 = 0 , |
k3 ×k3 = 0 |
||
можно использовать следующую компактную запись векторного произведения
krα ×krβ |
3 |
|
|
|
= ∑εαβγ krγ , α, β =1,2,3 , |
(1.1.4) |
|||
|
γ =1 |
|
|
|
|
|
1, еслиαβγ образуютчетную перестановку из123. |
||
где εαβγ |
= −1, еслиαβγ образуют нечетную перестановку из123. |
|||
|
|
0, если средиαβγ есть равныечисла. |
||
|
|
|||
Упражнение 1.1. Проверить следующие равенства: |
||||
а) |
εαβγ |
= εβγα = εγαβ |
(циклическая перестановка αβγ ), |
|
|
εβαγ |
= −εαβγ ,εγβα |
= −εαβγ |
, εαγβ = −εαβγ ; |
|
б) |
krσ = |
1 |
∑εαβσ krα ×krβ ; |
|
|
|
||||||
|
|
|
|
|
|||||||||
|
|
2 |
α,β |
|
|
|
|
|
|
|
|||
|
в) |
∑εαβσ εαβγ = 2δσγ . |
|
|
|
|
|
|
|||||
|
|
α, β |
|
|
|
|
|
|
|
|
|
|
|
|
С учетом (1.1.4) имеем для векторного произведения |
= ∑aαbβεαβγ krγ |
|
|
|||||||||
|
ar×br |
= (∑aαkrα ) ×(∑bβ kβ ) = ∑aα bβ kα ×kβ |
(1.1.5) |
||||||||||
|
|
α |
β |
|
α, β |
α,β ,γ |
|
|
|||||
так что компоненты этого вектора могут быть вычислены по формуле |
|
|
|||||||||||
(ar |
×br)γ = ∑εαβγ aαbβ |
, |
|
|
|
|
|
|
(1.1.6) |
|
|
||
|
α, β |
|
|
|
|
|
|
|
|
|
|
||
|
Смешанное произведение векторов a , b и cr = (c1,c2 ,c3 ) определяется формулой |
||||||||||||
|
r |
∑εαβγ aαbβ cγ = |
|
a1 |
a2 |
a3 |
|
|
|
|
|
||
|
|
|
|
|
|
||||||||
|
|
b1 |
b2 |
b3 |
|
|
|
|
|
||||
(a ×b) cr = |
|
|
, |
(1.1.7) |
|
|
|||||||
|
α,β ,γ |
|
|
c1 |
c2 |
c3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r |
r |
r |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
Эта величина равна объему параллелепипеда, построенного на векторах a |
, b |
, c , и не |
||||||||||
меняется при циклической перестановке сомножителей, т.е.
(a ×b) cr = (b ×cr) ar = (cr×av) b .
Вектор a ×(b ×cr) называется двойным векторным произведением. Имеем по
определению |
∑εαβγ εστβ aα bβ cτ kγ . |
a ×(br×cr) = ∑εαβγ aα (br×cr)β krγ = |
|
α,β ,γ |
α,β,γ ,σ ,τ |
Поскольку |
|
∑εαβγεστβ =∑εγαβεστβ =δγσδατ −δγτδασ ,
ββ
то |
r |
r |
|
|
|
|
r |
∑(δγσδατ −δγτδασ )aαbσ cτ kγ = |
|
||||
a |
×(b |
×c) = |
|
|||
|
|
r |
α,γ ,σ ,τ |
|
r |
|
= |
(∑bγ kγ )(∑aαcα ) − |
(∑cγ kγ )(∑aαbα ) = b (ar cr) − cr (ar b) . |
|
|||
|
γ |
|
α |
γ |
α |
|
Таким образом |
|
|
|
|||
|
ar×(b ×cr) = b (ar cr) − cr (ar b) |
(1.1.8) |
||||
Упражнение 1.2 Доказать, что
ar×(b ×cr) + b ×(cr×ar) + cr×(ar×b) = 0
Из (1.1.8) имеем для компонент вектора ar×(b ×cr) :
[ar×(b ×cr)]i = bi (∑aα cα ) − ci (∑aα bα ) , i = 1,2,3.
αα
При ортогональном преобразовании координат (xα → xα′ ,kα → kα′) компоненты aα |
|||||
r |
′ |
r |
= ∑aαkα |
′ ′ ′ ′ |
= δαi ) : |
вектора a |
преобразуются в aα |
по правилу (a |
= ∑aiki , kαki |
||
|
|
|
α |
i |
|
|
3 |
|
|
|
|
a′j = ∑Aji ai , Aji = k ′j ki′= cos(x′j , xi ) , |
|
(1.1.9) |
|||
|
i=1 |
|
|
|
|
Обратное преобразование |
|
|
|
||
|
3 |
|
|
|
|
ai |
= ∑Aki ak′ , |
|
|
|
(1.1.10) |
k =1

В дальнейшем вспомогательные сведения будут излагаться по мере возникновения необходимости.
2. Векторные функции скалярного аргумента.
Пусть a(t) = (a1 (t), a2 (t), a3 (t)) ,
где параметр t [0,T ], T ≤ ∞ .
|
|
|
Функция ar(t) : R1 → R3 |
|
|
|
называется вектор-функцией |
|
|
|
|
|
|
|
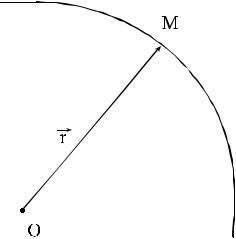
скалярного аргумента t. Если |
|
|
|
откладывать вектор a(t) в |
|
|
|
процессе его изменения от |
|
|
|
фиксированной точки O, то конец |
|
|
|
вектора будет описывать некоторую |
|
|
|
кривую, называемую годографом |
|
|
|
вектора a(t) . Приняв точку О за |
|
|
|
начало декартовой системы |
|
|
|
координат, получим следующее |
|
|
|
параметрическое уравнение |
xα = aα (t), α =1,2,3 , |
годографа: |
||
(1.1.11) |
|||
где aα (t) проекции вектора a(t) на оси координат. Производная по параметру t вектора a(t)
определяется как вектор, обозначаемый |
dar |
, с компонентами |
daα |
, где |
daα |
понимается в |
|||
dt |
|
|
|||||||
обычном смысле. |
|
|
dt |
dt |
|||||
|
|
|
|
|
|
|
|||
Таким образом, |
|
|
|
|
|
|
|
||
da |
= lim |
av(t + ∆t) − a(t) |
< ∞ |
|
|
|
|
(1.1.12) |
|
dt |
∆t →∞ |
∆t |
|
|
|
|
|
|
|
Производные высших порядков определяются аналогично.
Следует отметить, что вектор dar направлен по касательной к годографу. Действительно (см. dt
рис.), пусть значению t отвечает точка M годографа вектор-функции a(t) . Вектору
a(t) + ∆a = a(t + ∆t) соответствует на годографе точка M ′, а ∆a - приращение a(t) , соответствующее приращению ∆t .
∆a
Приращение ∆t есть вектор, направленный
по секущей MM ′. При ∆t → 0 точка M стремится к M ′ , а секущая MM ′ стремится к касательной к годографу в точке M .
Потому вектор dar направлен по касательной dt
к годографу вектор-функции a(t) .
Следующие свойства операции дифференцирования вектор-функций проверяются по определению:
а) Если ar(t) = ∑n ari (t) , то
i =1
dar |
n |
dar |
(t) |
|
|
|
|
|
= ∑ |
i |
|
, |
|
|
(1.1.13) |
dt |
dt |
|
|
||||
i=1 |
|
da |
= ∑daα krα |
||||
б) Если ar(t) = ∑aα (t) kα , kα = const , то |
|||||||
|
α |
|
|
|
dt |
α |
dt |
в) Если ar(t) =ϕ(t) b(t), ϕ(t) -скалярная функция, то
dar |
= |
dϕ r |
|
|
|
db |
|
|
|
|
|
|
||
dt |
dt |
b(t) +ϕ |
dt |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) Если ϕ(t) = ar(t) b(t) , то |
|
|
|
|
|
|||||||||
dϕ |
|
r |
db |
|
r |
|
dar |
|
|
|
|
|
|
|
dt |
= a(t) dt |
|
+ b(t) |
dt |
|
|
|
|
|
|
||||
|
|
r r |
|
r |
|
|
dcr |
dar r |
r |
db |
r |
|
||
д) Если c |
= a |
×b |
,то |
dt = |
dt |
×b |
+ a |
× dt |
= −(b |
× |
||||
r
ddta + ddtb ×ar) .
3. Координатный, векторный, естественный способы описания движения материальной точки.
Изучение теоретической механики начинается с анализа движения материальных точек и тел независимо от причин, вызывающих эти движения. Этот раздел теоретической механики называется кинематикой. Основной задачей его является изучение законов движения материальных точек и их систем как геометрических объектов. Любое материальное тело можно рассматривать как совокупность материальных точек. Поэтому кинематика делится на две части: кинематика точки и кинематика твердого тела. Далее, под движением понимается изменение положения тела относительно других тел с течением времени. Так как в природе нет неподвижных тел, то всякое движение относительно. В классической механике постулируется существование "условно" неподвижного тела и, следовательно, существование системы отсчета, по отношению к которой будем говорить об абсолютном движении материальных тел. Эту систему отсчета будем называть неподвижной.
Движение точки в пространстве можно описать с помощью трех основных способов: векторного, координатного, естественного. Все три способа эквивалентны.
а) Векторный способ. Движение точки М относительно неподвижной точки О определяется
→ |
r |
(t) , сопоставленному |
радиус-вектором OM |
≡ r |
каждому моменту времени t, т.е.
r = r (t) , |
(1.1.14) |
Относительно гладкости r (t) предполагается,
что r (t) непрерывна и дважды дифференцируема:
rr(t) C2[0,T ] . Уравнение (1.1.14) определяет
положение точки М в любой момент времени t или, как говорят - определяет закон движения точки М.
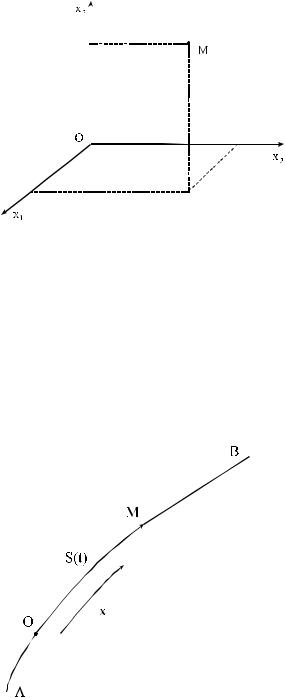
Кривая, описываемая точкой М в пространстве, называется траекторией движения точки. Траектория движения является, очевидно, годографом радиус-вектора точки М, а (1.1.14) есть векторная запись уравнения траектории.
б) Координатный способ. В системе координат Ox1x2 x3 положение точки М в каждый момент |
||
|
времени определяется тремя координатами |
|
|
||
|
xα как функциями времени t: |
|
|
xα = xα (t), α =1,2,3; |
(1.1.15) |
|
Уравнения (1.1.15) называются |
|
|
кинематическими уравнениями движения |
|
|
точки. Они являются параметрической |
|
|
формой уравнения траектории движения |
|
|
точки М. |
|
|
Возможно использование и других |
|
форм записи уравнений движения точки. Например в полярной системе (r,ϕ) таковыми |
||
являются уравнения r = r(t),ϕ =ϕ(t) . Связь векторного и координатного способов очевидна.
|
→ |
= ∑xαkrα , где kα - орты системы |
Если уравнения (1.1.15) заданы, то радиус-вектор OM |
||
|
|
α |
r |
→ |
|
Oxα . Если же r |
= OM задан, то в подходящем базисе, в силу единственности представления |
|
вектора, однозначно определяются компоненты r (t) и, следовательно уравнения (1.1.15).
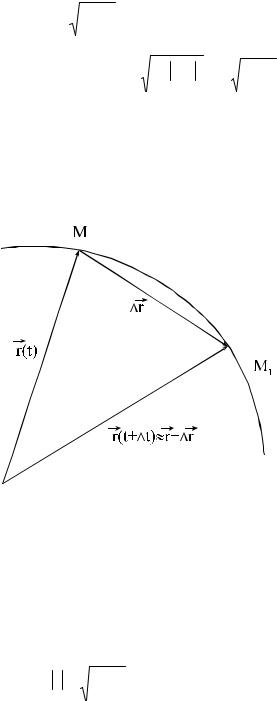
в) Естественный способ. Пусть кривая АВ - известная траектория точки М. Выберем начальную точку О и условимся полагать одно направление
от точки О положительным, а другое - отрицательным. Выберем масштаб. Тогда положение точки М на ее траектории можно
определить дуговой координатой ОМ, которую еще называют расстоянием точки М от начала О. Движение точки будет определено, если для любого t будет известна дуговая координата s, т.е.
(1.1.16)
Предполагается, что S C2[0,T ] . Уравнение
(1.1.16) определяет закон движения точки по траектории, но не в пространстве. Закон движения
точки в пространстве определяется совокупностью всех факторов: траекторией движения (ее "формой" и положением в пространстве), положением начальной точки О на траектории с указанием положительного направления, линейным масштабом и уравнением (1.1.16). Если известны координаты точки (и, следовательно, радиус-вектор), то дуговая координата определяется элементарно:
t |
|
|
|
|
|
|
|
S = S0 ± ∫ |
|
&2 |
|
|
|
|
(1.1.17) |
∑xα dt , |
|
|
|
|
|||
t0 |
α |
|
|
|
|
|
|
где S0 = S(t0 ) |
2 |
= ± |
&2 |
& |
dxα |
. |
|
, ds = ± ∑dxα |
∑xα dt , xα ≡ |
dt |
|||||
|
|
α |
|
α |
|
|
|
Выбор знака определяется направлением отсчета. Обратный переход от естественного описания к векторному (координатному) будет изложен в лекции 4.
4. Кинематические характеристики: скорость, ускорение.
4.1. Скорость. Рассмотрим два близких положения M и M1 материальной точки,
соответствующих t и t + ∆t . Им
соответствуют радиус-векторы rr и rr + ∆→r .
Вектор → 1 = ∆r есть приращение за
)
t
(
r
r
MM
время ∆t . Среднюю скорость точки M
определяют как отношение ∆r к ∆t .
Истинная же скорость точки в момент t есть вектор
vr ≡ lim |
∆r |
= |
dr |
, |
(1.1.172) |
|
∆t |
dt |
|||||
∆t→0 |
|
|
|
Поскольку производная любой вектор-
функции направлена по касательной к годографу, то v направлен по касательной к траектории.
В системе координат Oxα , α =1,2,3 |
|
|
|
|
r |
r |
& |
= ∑vαkα . |
||||
, вектор r |
= ∑xαkα . Поэтому v |
= ∑xαkα |
||||||||||
|
|
|
|
|
|
|
|
|
|
α |
α |
α |
Проекции вектора скорости на оси координат равны |
|
|
||||||||||
& |
& |
|
dxα |
|
|
|
|
|
|
|
|
|
vα = xα , |
xα |
≡ |
|
, α =1,2,3 |
|
|
(1.1.18) |
|
||||
dt |
|
|
|
|||||||||
Модуль |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
& |
|
|
|
|
|
|
||
|
&2 |
, cos(v, xα ) = |
xα |
|
, |
|
(1.1.19) |
|
||||
|
|
r |
|
|
|
|
||||||
v = ∑xα |
|
|
|
|
|
|||||||
α |
|
|
|
|
|
v |
|
|
|
|
|
|
Скорость в естественном описании. Пусть известна траектория и уравнение движения по траектории S = S(t) . Каждой точке траектории соответствует определенный радиус-вектор r , но каждая точка траектории определяется дуговой координатой S. Поэтому можно
рассматривать r |
как сложную функцию вида r = r[s(t)] . Тогда, следуя (1.1.17), получим |
||||||||
r |
= |
dr |
= |
ds dr |
& |
r |
≡ |
dr |
(1.1.20) |
v |
dt |
dt ds |
= sτ1 |
, τ1 |
ds |
||||
|
|
|
|
|
|
|
|||

где τr1 - единичный вектор касательного к траектории направления. То, что τ1 касательный вектор есть свойство производной радиус-вектора. Рассматривая отношение ∆rr - длины хорды
MM1 , к |
|
∆S |
|
- длины дуги MM1 , убеждаемся в том, что |
|
τv1 |
|
|
=1. Если обозначить |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
& |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
= v |
r |
. |
|
|
|
|
|
|
|
|
||||||
S |
= v τ |
1 |
≡ v , то (1.1.20) можно придать вид: v |
τ |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
τ1 |
|
|
|
|
|
|
|
|
|
|
|
|
τ1 |
|
|
|
|
|
|
|
|
|
|
||||||||
4.2. Вектор ускорения вводится аналогично вектору скорости. Рассмотрим скорости точки M в |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
моменты t |
и t + ∆t . Совмещая начало |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторов v(t) и v(t + ∆t) в точке M , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находим приращение ∆v скорости за время |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆t . По определению отношение ∆v |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называется средним ускорением arср за |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
время ∆t . Этот вектор коллинеарен вектору |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆v и направлен в сторону вогнутости |
|||||||||||||
траектории. Если существует предел указанного отношения при ∆t → 0 , то этот вектор |
||||||||||||||||||||||||||||||||||||||
называется ускорением точки в момент времени t |
и обозначается |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
r |
= lim |
∆vr |
= |
dvr |
= |
d 2rr |
, |
|
|
|
|
|
|
|
|
|
|
|
|
(1.1.21) |
|||||||||||||
|
|
|
|
a |
|
∆t |
dt |
dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
∆t →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В декартовой системе Oxα |
имеем для ar = (a1,a2 ,a3 ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
& |
|
&& |
|
|
|
|
r |
2 |
|
r |
|
|
|
|
|
|
|
aα |
|
|||||||||||
|
|
|
|
|
|
|
|
|
α =1,2,3 ; |
a = |
∑aα ; |
cos(a, xα ) |
= |
|
r |
|
. |
|||||||||||||||||||||
|
|
|
|
aα = vα |
= xα , |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
Для представления ускорения в естественном описании, вектор τ1 |
= |
dr |
снова рассмотрим как |
|||||||||||||
ds |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сложную функцию τ1[s(t)] . Следуя (1.1.21) и (1.1.20), получим |
|
|
|
|||||||||||||
r |
|
dvr |
r |
|
|
|
d 2s |
ds 2 |
dτr |
|
|
|
||||
a |
= |
|
=τ |
1 |
|
|
+ |
|
1 |
|
|
|
||||
dt |
dt2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
dt |
ds |
|
|
|
|||||
Поскольку |
|
τr1 |
|
|
=1, то годографом τr1 является кривая, лежащая на поверхности сферы |
|||||||||||
|
|
|||||||||||||||
единичного радиуса. Производная ddsτ1 должна быть направлена по касательной к окружности
и, следовательно, ортогональна τr1 (к кривой r = r (s) ). Это направление называется главной нормалью к кривой. Если τr2 - единичный вектор нормали (направлен в сторону вогнутости кривой), то
dτ1 |
= kτr |
= |
1 |
τr |
, |
(1.1.22) |
|
ds |
ρ |
||||||
2 |
|
2 |
|
|
