Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1.Папин А.А. Теоретическая механика

.pdf

Скачиваний:

Добавлен:

14.05.2015

Размер:

1.19 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

v dτv3

v dτv2

v v

dτv2

drr

d 2 rr dρ

d 2 rr

d 3 rr

= −τ2

=τ2

×τ1

=τ1 τ2 ×

2 + ρ

= ∑ d 2 x2α

2 .

Таким образом

σ = {σαβ }

− k

0 χ

− χ

Формулы (1.3.3) получены.

Напомним следующие два известных факта.

Лемма 1. Для того, чтобы линия была прямой необходимо и достаточно чтобы кривизна была

равна нулю.

Доказательство. Пусть τr и rr0 - постоянные векторы. Параметрическое уравнение прямой есть

rr =τrs + rr0 . Тогда

d 2 rr

dτr

τ2

= 0 k = 0 .

ds2

d 2 rr

Если же k = 0

, то

= 0

и, следовательно, r =τs + r .

ds2

Лемма 2. Для того, чтобы линия была плоской необходимо и достаточно, чтобы кручение было равно нулю.

Доказательство. Пусть линия лежит в плоскости (τr1 ,τr2 ) и, следовательно, в любой ее точке

τr3 = const . Но тогда − χ τr2 = dτr3 = 0 . ds

Если же χ = 0 , то dτr3 = 0 и τr3 = const = ar. Из равенства ds

τr1 τr3 = ar ddsr = d(ads r ) = 0

следует ar rr = const , т.е. ∑aα xα = const . Это и означает, что все точки кривой лежат в одной плоскости.

2. Связь естественного описания с координатным. Гамма матрица.

Чтобы установить указанную связь необходимо получить представление векторов

естественного базиса через декартовый базис, т.е. получить соотношения вида
τrα	= ∑γαβ krβ ,	(1.3.6),
	β
где γαβ	= γαβ (s) - суть элементы γ -матрицы.

Используя символику, введенную в Лекции 1, а также свойства векторов естественного базиса, выясним свойства γ -матрицы. Во-первых, заметим, что

r	r	r			r			r	r r		r
τ1	=τ2	×τ3	=	∑γ 2β kβ		×	∑γ 3σ kσ		= ∑γ 2βγ 3σ kβ ×kσ	= ∑γ 2βγ 3σ ∑εβσα kα .
				β			σ		β ,σ	β ,σ	α

Поэтому τr1 = ∑γ1α krαα

γ1α = ∑εβσαγ 2βγ 3σ .

β,σ

В частности

= ε

+ε

γ 22 γ 23

231

321

γ 23

γ 21

γ 22

Рассматривая τr2

=τr3 ×τr1 , τr3

=τr1 ×τr2 , аналогично получим

γ13

γ12

γ11

γ13

γ12

γ11

γ12

γ13

γ11

γ12

Таким образом, любой элемент γ ij

равен своему алгебраическому дополнению. Далее, условие

∑γ

δαβ =τ

τβ

ασ kσ

∑γ βω kω

= ∑γαβγβωkσ krω = ∑γασγβωδσω = ∑γασγβσ

σ ,ω

Приводит к следующей системе уравнений

(У1)

+γ 2

(У4)

γ γ

+γ

= 0

(У2)

+γ 2

(У5)

γ γ

+γ

+γ γ

= 0

(У3)

+γ 2

(У6)

γ γ

+γ

+γ γ

= 0

Эта система содержит 9 неизвестных. Поэтому три из них можно считать независимыми, а остальные выразить через независимые. В качестве таковых берем, например, γ13 , γ 31 , γ 33 .

Схема решения системы. Из (У3)

γ32 = + 1−γ 312 −γ 332

(Если брать "-", получим другой набор решений). Исключая γ11 из (У1), (У6), находим

γ		= −	γ	13	γ	33	1 −γ	2	−γ	2	+γ	31	1 −γ 2	−γ	2
γ	12	= −		13		33		31		33		31	13		33
	12								1	−γ 332
и возвращаясь в (У6):									1	−γ 332
и возвращаясь в (У6):
γ	11	=	(1 −γ 312				−γ 332 )(1 −γ132 −γ 332 )−γ 13γ 31γ 33
γ		=							1−γ 332

Осталось выразить γ 21, γ 22, γ 23 . Сначала (У4), (У5) рассматриваются относительно γ 21 и γ 22 :

γ =	γ 12γ 33−γ 13γ 32				γ ;	γ =	γ 13γ 31−γ 11γ 33				γ

21	γ γ −γ γ			12	23	22	γ γ	−γ γ		31		23
	11	32	31				11	31	12
Заменяя γ 12, γ 32		найденными выше выражениями через независимые γ 13, γ 31, γ 33 , получим

γ 21= −

γ 23

(γ 31γ

1 −γ132 −γ 332 +γ

1 −γ 312 −γ 332 )

∆

33 (1 −γ132 −γ 332

)(1 −γ 312 −γ 332 )

22= −

γ 13γ 31−γ

( * )

∆

∆ =γ 11γ 32−γ 31γ 12

Подставляя γ 21 , γ 22

в (У2) для γ 23 получим

Откуда

γ 232 =1 −γ132 −γ 332 .

γ23 = − 1−γ132 −γ332

Снова возвращаясь к ( * ):

γ γ

1 −γ 2

−γ 2

+ 1 −γ 2

−γ 2

31 33

1 −γ 332

γ 33 (1 −γ132 −γ 332 )(1 −γ 312 −γ 332

)−γ13γ 31

1 −γ 332

Итак, элементы γ -матрицы выражены через три независимых элемента γ13 , γ 31 , γ 33 . Это

означает, что можно выбрать три независимых параметра, через которые можно выразить все элементы γ -матрицы. За эти три параметра Эйлер предложил брать три угла ϕα , α =1,2,3 ,

носящие теперь его имя.

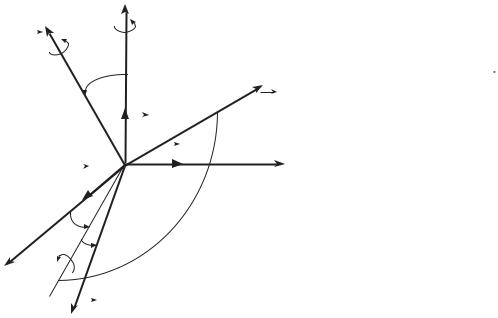
Лекция 4 Углы Эйлера. Переход от естественного способа к координатному.

1. Углы Эйлера.

Для вычисления элементов γαβ гамма – матрицы через углы Эйлера ϕ1, ϕ2, ϕ3 совместим начала системы Ox1x2x3 и естественного базиса Mτ1τ2τ3 .

Пусть MN – линия пересечения (линия

узлов) плоскостей x3=0 и τ3=0.

Введём следующие углы (углы

Эйлера):

ϕ1 – угол прецессии (между k1 и

линией узлов MN);

ϕ2 – угол чистого вращения (между τ 3

и k 3 );

ϕ3– угол нутации (между τ 1

и линией

узлов MN);

2 ,kr

Перевести триэдр k1,kr

в триэдр

τ 1,τ 2 ,τ 3

можно с помощьюrтрех

поворотов: на ϕ1 вокруг оси k

3 , затем на

угол ϕ2 вокруг оси MN, на угол ϕ3 вокруг

осиτ 3 . За положительное направление

отсчёта углов принимается направление

вращения против хода стрелки часов

вокруг соответствующих осей.

а)

поворот на ϕ1 [0,2π] вокруг

k 3

; посредством этого ортогонального преобразования

орты

kα

переходят в орты

τr'α , причём ( k 3

- неподвижна)

= ∑γ '

ασ kσ

cos ϕ1

sin ϕ1

ϕ1

cos ϕ1

γ ' =

− sin

б) поворот на угол ϕ2 [0,π] вокруг MN; орты τr'α

переходят в орты τr''α , причём

= ∑γ ''

τ ''

βα τ

cosϕ2

γ ''=

sinϕ

−sinϕ

cosϕ2

в) поворот на угол ϕ3 [0,π] вокруг оси τr3 ; орты τr''ω переходят в орты τrω , причём

rω = ∑γ '''

ωβ τ ''

cosϕ

sinϕ

γ ''' = −sinϕ3

cosϕ3

Врезультате орты kα переходят в τα , причём

τω	= ∑γ	ωσ kσ	,	(1.4.1)
	σ	ωσ kσ

γωσ

= ∑γ'''ωβ γ''βα γ'ασ ,

(1.4.2)

βα

Подробнее

{

cos ϕ cos ϕ −sin ϕ cos ϕ sin ϕ

sin ϕ cos ϕ + cos ϕ cos ϕ sin ϕ

sin ϕ sin ϕ

}= −cos

1 sin

3 −sin

1 cos

2 cos

−sin

1 sin

3 + cos

1 cos

2 cos

sin

2 cos

ωσ

ϕ ϕ

ϕ ϕ ϕ

ϕ ϕ ϕ ϕ ϕ

sin ϕ sin ϕ

−cos ϕ sin ϕ

cos ϕ

Таким образом, введённая в Лекции 3, γ - матрица определяется тремя углами Эйлера ϕ1, ϕ2, ϕ3. Верно и обратное: если заданы элементы γαβ, то определяются углы Эйлера , т.к. из равенств

γ13=sin ϕ2*sinϕ3 → ϕ3,				γ31=sin ϕ1*sinϕ2 → ϕ1,				γ33=cos ϕ2 → ϕ2
γ23=sin ϕ2*cosϕ3,					γ32=-cos ϕ1*sinϕ2
Следует, что				γ13						γ 32
cos ϕ2=γ33,	sin ϕ3		=	γ13	,			cosϕ1	=	γ 32
cos ϕ2=γ33,	sin ϕ3		=	1 −γ 332	,			cosϕ1	=	1 −γ 332
				1 −γ 332						1 −γ 332
cosϕ3 =	γ 23	,			sin ϕ1	=	γ	31
cosϕ3 =	1 −γ 332	,			sin ϕ1	=	1 −γ 332
	1 −γ 332						1 −γ 332

Тем самым, между γαβ и ϕα существует взаимнооднозначное соответствие. В Лекции 3 было

показано следующее равенство:		∑γασ γ βσ =δαβ ,	(α,β)=1,2,3.
		σ
Поэтому, если P – обратная к γ матрица, т.е.			∑γασ Pσβ =δαβ
			σ
то	Pσβ=γβσ,	((σ,β)=1,2,3).

Это означает что, P= γ*, т.е. обратная и транспонированная матрицы совпадают.

Следовательно, γ - матрица является ортогональной. Заметим также, что

γωσ =τrω • kσ = cos(τrω , kσ )

т.е. элементы γωδ совпадают с косинусами углов между естественными и неподвижными осями. Заметим также, что для kσ в базисе τσ справедливо разложение

kσ	= ∑γωσ τrω ,	(1.4.3')
	ω

2. Переход от естественного способа к координатному.

Пусть движение точки задано естественным способом, т.е. задана траектория, определяемая естественными уравнениями k(s), χ(s), и уравнение движения по траектории s = s(t). Найти по этим данным декартовы координаты точки как функции времени, т.е. xα=xα(t), α=1,2,3. Для решения этой задачи заметим, что для τr1 из определения и формулы (1.4.1) справедлива

следующая цепочка равенств

τr1 =

dτ

= ∑

d xσ

= ∑γ

kσ

1σ k

d xσ

откуда

= γ1σ ,

σ=1,2,3.

Используя вид γ - матрицы эту систему запишем подробнее

d x1

=γ

= cosϕ1 cosϕ3 −sinϕ1 cosϕ2 sinϕ3

d x2

=γ

= cosϕ1 cosϕ3 + cosϕ1 cosϕ2 sinϕ3 ,

(1.4.3)

d x3

=γ

= sinϕ2 sinϕ3

Далее, в формулах Френе

d τr1

d τr2

d τr3

= kτ 2 ,

= −kτ1 +

χτ 3

= −χτ

Заменим все τrα

через γ - матрицу. Тогда получим систему 9 уравнений

d γ1σ

= k γ 2σ ,

d γ 2σ

= −k γ1σ + χ γ

3σ ,

d γ3σ

= −χ γ 2σ

из которых всего 3 независимых. Берём последние из каждой группы уравнений, кроме

последней, где берём второе (σ=2):

d γ13

= k γ 23 ,

d γ 23

= −k γ13 + χ γ33 ,

d γ32

= −χ γ 22 ,

(1.4.4)

Если воспользоваться представлениями γαβ через углы Эйлера, то вместо (1.4.4) получим

ϕ sin

d ϕ

+sin ϕ cos ϕ

d ϕ

= k sin ϕ cos ϕ

cos

d ϕ

ϕ cos ϕ

−sin ϕ sin ϕ

= χcos ϕ − k sin

ϕ sin ϕ

cos

(1.4.5)

ϕ1

ϕ2

= −χ(−sin ϕ sin ϕ + cos ϕ cos ϕ cos ϕ )

sin ϕ sin ϕ

−cos ϕ cos

Разрешая эту систему относительно

d ϕα

, α=1,2,3, окончательно приходим к следующей

системе

sin ϕ

d ϕ

= χ

sin ϕ

d ϕ

= χcos ϕ

(1.4.6)

d ϕ

= k −χsin ϕ ctg ϕ

Замечание.

Пусть вектор - функция U=(u1(x),…,un(x)) удовлетворяет уравнению

=f(x,u1,…,un),

f=f(f1,…,fn)

и начальным условиям

U(x0)=U0. Если f

непрерывна по всем переменным и непрерывно -

дифференцируема по U в окрестности (x0,U0), то в окрестности (x0,U0) существует единственное решение U, удовлетворяющее уравнению и начальным условиям.

Рассмотрим систему (1.4.3), (1.4.6) при начальных условиях α (	s0	) = α0	, ϕ	α	(	s0	) =ϕ0	при
x	s0	x		α		s0	α

s=s0 (α=1,2,3) , т.е. определена начальная точка траектории M0 и начальная ориентация Эйлеровых углов. В силу замечания справедлива следующая теорема.

Теорема. Если заданы кривизна и кручение как непрерывно – дифференцируемые функции расстояния на траектории, то существует единственная линия с этими характеристиками, проходящая через заданную точку M0 и обладающая в этой точке заданным трёхгранником Френе.

В силу этой теоремы система (1.4.3),(1.4.4) имеет единственное решение xα=xα(s), ϕα=ϕα(s). Подставляя в эти функции s = s(t) получим искомую зависимость координат xα от времени: xα=xα[s(t)].

Лекция 5. Кинематика твёрдого тела. Формулы Пуассона. Угловая скорость, формулы Эйлера. Линейные скорости точек твёрдого тела. Угловое ускорение. Линейные ускорения точек твёрдого тела.

Материальная точка есть простейшая модель классической механики. Более общей является модель абсолютно твёрдого тела. Основной задачей кинематики твёрдого тела является задача определения в любой момент времени координат произвольной точки твёрдого тела, её скоростей и ускорений, в том числе и угловых.

1. Кинематика твёрдого тела.

Возможны различные способы описания движения точек твёрдого тела. Изложим один из таких подходов. Пусть движение твёрдого тела происходит относительно абсолютной

(неподвижной) системы координат

x1 x2 x3 (см. рис.).

В теле выделяется точка

O (полюс), с которой

связывается система

координат Oξ1ξ2ξ3,

произвольно

ориентированная

относительно системы

Ox1x2 x3 . В дальнейшем

€

kα , kα

(α=1,2,3) орты

соответственно системы

x1x2 x3

и Oξ1ξ2ξ3. Пусть

Ox1′x′2x′3

– система

координат, полученная

паралельным переносом

Ox1x2 x3

в точку O. Следуя

Лекции 4, введём углы

определяющие ориентацию системы Oξ1ξ2ξ3 относительно Ox1′x′2x′3

Эйлера ϕα (α=1,2,3),

и, следовательно,

относительно Ox1x2 x3 . Такое задание углов Эйлера и положение точки O в любой момент

времени позволят определить положение твёрдого тела также в любой момент времени. Соотношения (α=1,2,3):

α0	=	α0	(t) , ϕα=ϕα(t),	r	= (	0	,	0	,	0) ,	(1.5.1)
x		x		r 0		x1		x2		x3

называются уравнениями движения твёрдого тела. Рассмотрим произвольную точку M твёрдого тела, имеющую в системе Oξ1ξ2ξ3 координаты (ξ1,ξ2,ξ3). Пусть rr = OM , rr0 = OO ,

ρr = OM . Очевидно, что

rr = rr0 + ρ							(1.5.2)
есть уравнение движения точки M твёрдого тела. Заметив, что
r = ∑ α	kα	, r	= ∑ α0	kα	,	ρ = ∑ξ	€
x	kα	r0	x	kα		β	β kβ
α			α			β
а так же, в силу (1.3.6),	k€β	= ∑γ βσ kσ
		σ
получим следующую форму (1.5.2):
xα = xα0 + ∑ξβ γ βα ,							(1.5.3)
β

Таким образом, движение твёрдого тела определяется заданием шести параметров из (1.5.1), т.е. имеет шесть степеней свободы.

2. Формула Пуассона.

При движении твёрдого тела направляющие орты €α системы координат O 1 2 3, очевидно, k ξ ξ ξ

изменяются во времени (относительно неподвижной системы координат). Рассмотрение скорости изменения этих векторов приводит к понятию угловой скорости твёрдого тела.

€

Поскольку производная от kα по времени является также вектором, то имеет место следующее

представление:

d €

kα

= ∑ω€αβ

€ ,

(1.5.4)

kβ

в котором элементы ω€αβ

€

являются неизвестными. Умножая (1.5.4) скалярно на kσ , найдём,

€

d kα

что

ωασ =

kσ

α,σ =1,2,3.

€

Далее, из равенства

(€

€ )

(δασ )=

0 =

d kα

€

d kσ

€

=ω€ασ +ωrσα = 0 следует

kα

kσ

kα

антисимметричность матрицы {ω€ασ}и, следовательно,

ω€12

ω€13

−ω€12

{ωασ}=

ω€23

−ω€13

−ω€23

Положим

ω€1 ≡ω€23 ; ω€2 ≡ω€31 ; ω€3 ≡ω€12 ,

(1.5.5)

Определение.

€

(1.5.6)

Вектор ω = ∑ω€αkα ,

Называется вектором угловой скорости твёрдого тела.

Использование ε объекта (Лекция 1) позволяет придавать (1.5.5) следующий вид

ω€α	= 1	∑εσταω€στ ,	(1.5.7)
	2	στ
Или, обратное представление,
ω€αβ	= ∑εαβσω€σ ,		(1.5.8)

Непосредственной проверкой (используя (1.5.4) и (1.5.8)) можно убедится в справедливости

следующих равенств:			€
			€		€				€
во – первых:			dkα	= ∑εαβσ	€				€
во – первых:			dt	= ∑εαβσ	ω€σ kβ	= ∑εστβω€σδατ kβ
			dt	σβ		στβ
и, во – вторых			€	€	r	€	r		€	€
и, во – вторых			( kα	= ∑δατ kτ	): ω	×kα	=ω	×	∑δατ kτ	= ∑ω€σ kβδατεστβ
				τ					τ	στβ
Совпадение правых частей этих равенств означает, что справедливы формулы
€	r	€
dkα	r	€
dt	=ω	×kα ,								(1.5.9)

носящие имя Пуассона.

3. Формулы Эйлера.

Эти формулы позволяют представить компоненты угловой скорости через углы Эйлера. Они имеют вид

	= ω€23	= ∑γ&2τγ3τ = ϕ&1 sin ϕ2 sin ϕ3 + ϕ&2 cos ϕ3
ω€1	= ω€23	= ∑γ&2τγ3τ = ϕ&1 sin ϕ2 sin ϕ3 + ϕ&2 cos ϕ3
	= ω€31	τ	(1.5.10)
ω€2	= ω€31	= ∑γ&3τγ1τ = ϕ&1 sin ϕ2 cos ϕ3 − ϕ&2 sin ϕ3 ,	(1.5.10)
		τ
ω€3	= ω€12	= ∑γ&1τγ2τ = ϕ&1 cos ϕ2 + ϕ&3
		τ
		τ

где γατ - компоненты γ - матрицы, выраженные через углы Эйлера ϕ1, ϕ2, ϕ3, γ&ατ = dtd γατ

(см. Лекцию 4).

Для доказательства (1.5.10) сначала выразим с помощью γ - матрицы орты

€	r
kσ	= ∑γστ kτ
	τ

€

kσ через kσ :

€

dkσ

Поэтому

= ∑γστ kτ

а для элемента ω€ασ

в этом случае имеем

€

ω€ασ =

dkα

= ∑γ&ατ kτ ∑γσλkλ = ∑γ&ατγστ

kσ

Последнее и приводит к (1.5.10). Этим формулам

можно придать наглядную механическую

k2 интерпретацию. Пусть n - орт линии узлов ON. Он

лежит в плоскости ξ1,ξ2 и поэтому

€

где

€

=αk1

βk2

α = n k1 = cosϕ3

€

= cos(

+ϕ3 )

= n

Тем самым

€

(1.5.11)

= cosϕ3k1

_ sinϕ3k2

Если же воспользоваться (1.5.10):

€ €

€

ϕ2 cos ϕ3

€

& €

ω = ∑ωαkα = ϕ1

(k1 sin ϕ2 sin ϕ3 + k2 sin

+ k3 cos

ϕ2 )+ ϕ2

(k1 cos ϕ3

− k2 sin

ϕ3 )+ ϕ3k3

то нетрудно увидеть, что выражение в первой скобке есть

€

k3 = ∑γλ3kλ ,

а вторая даёт вектор nr. Поэтому

ωr = ∑ωrα ,

(1.5.12)

где

- угловая скорость прецессии,

ω1

= ϕ1k 3

& r

ω2

=ϕ2n - угловая скорость нутации,

& €

- угловая скорость собственного вращения.

ω3

= ϕ3k3

Таким образом, угловая скорость твёрдого тела “складывается” из угловых скоростей

€

и Oξα.

вращений вокруг k3 , n

, k3 , в результате которых и происходит совмещение Oxα

Рассмотрим наконец угловую скорость в неподвижной системе

xα . Для получения

€

по уже

компонент ω в этой системе достаточно в (1.5.12) орты n иk3

заменить через k3

известной формуле

€

= ∑γσβ kβ

kσ

Однако, проще заметить, что для орта n , лежащего в плоскости x1,x2 имеет место

разложение

nr =α1k1 + β1k2

где

= cosϕ ,

−ϕ

= n k

= n

= cos

= sinϕ

Кроме того

€

= ∑γ3β kβ

Тогда вместо (1.5.12) получим

ωr = ∑ωα kα ,

(1.5.13)

где

ϕ3 sinϕ2 sinϕ1 +ϕ2 cosϕ1

ω1 =

(1.5.14)

ω2

ϕ3 sinϕ2 cosϕ1 −ϕ2 sinϕ1 ,

ϕ3 cosϕ2 +

ϕ1

ω3

Эти формулы, так же как и (1.5.10), носят имя Эйлера.

Величина угловой скорости

ωr =

∑ω€α

2 =

∑ωα

= ϕ&12 +ϕ&2

2 +ϕ&3

2 + 2ϕ1ϕ3 cosϕ2

(1.5.15)

Из (1.5.10) или (1.5.14) следует, что компоненты угловой скорости однозначно определяются заданием углов Эйлера.

Верно и обратное: задание угловой скорости и начального положения углов Эйлера позволяют определить последние в любой момент времени. Действительно, разрешая (1.5.10)

или (1.5.14) относительно ϕ&α , получим (разрешимость проверяется элементарно) нормальную систему обыкновенных дифференциальных уравнений вида ϕ&α =φα (ωβ ,ϕβ ), (α,β)=1,2,3.

Разрешимость задачи Коши для этой системы следует из соответствующей теоремы для систем общего вида (см. Замечание в Лекции 4).

Упражнение. Доказать, что угловая скорость ω не зависит от выбора полюса т. O. (От противного).

4. Линейные скорости точек твёрдого тела.

Пусть rr = OM – радиус-вектор произвольной точки M твёрдого тела, rr0 – радиус-вектор полюса O, ρ – радиус-вектор точки M в системе Oξ1ξ2ξ3 (см. рис. п.1). Имеем

+ ∑ξ

€

(1.5.16)

= r0

+ ρ = ∑xα k α

α k α ,

По определению вектора скорости точки M:

0 r

€

dr0

dρ

V =

∑ξα k α ,

(1.5.17)

= ∑xα k α +

Первое слагаемое правой части (1.5.17) есть скорость полюса V0 , а для второго, с учётом

формул Пуассона (1.5.9), имеем (ξα=const в системе Oξ1ξ2ξ3):

€

dρ

dkα

= ∑ξα

= ∑ξαω

×kα =ω

×∑ξα kα =ω

× ρ

Поэтому

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.12.2018257.02 Кб271. Криминалистика как наука.doc
#
09.09.201958.37 Кб201. Социально-экономическое развитие в 1964-1982...doc
#
18.03.201621.17 Кб811. частное право.docx
#
14.05.2015457.22 Кб271.doc
#
14.05.2015154.11 Кб171.doc
#
14.05.20151.19 Mб491.Папин А.А. Теоретическая механика.pdf
#
16.07.201975.26 Кб211.Семилет - Деминовой заоч Культуролог.doc
#
03.09.201955.81 Кб1810 пунктов Фашистской политики.doc
#
19.12.201880.19 Кб2410-20.docx
#
12.09.2019173.06 Кб710-Рабочие программы учебных дисциплин.doc
#
16.11.201983.97 Кб1210. Иоанн де Мурис.doc