5.9. Несобственные интегралы

Известно несколько приемов вычисления разных типов несобственных интегралов [1]. Иногда удается заменой переменных перейти от интеграла с бесконечными пределами к интегралам с конечными пределами. Eсли подынтегральная функция после преобразования останется конечной на новом интервале, то для интегрирования можно использовать методы программы, рассмотренные в предыдущих разделах.

Довольно распространенным является способ образования верхней предела интегрирования, при котором исходный несобственный интеграл разбивается на сумму двух интегралов

Затем оценивается аналитическими, а иногда и численными методами модуль второго интеграла и при выполнении условия

в качестве приближенного значения несобственного интеграла выбирается величина интеграла в пределах [0,b].

Для вычисления несобственных интегралов с бесконечными пределами применимы и квадратурные формулы Гаусса-Кристоффеля (5.47), узлы и веса которых определяются в зависимости от вида весовой функции (х), входящей под интеграл в форме произведения (х) • f(x).

Так, для интегралов в пределах [0,] при (х)=хехр(-х) узлами квадратурной формулы (5.47) являются корни многочленов Лаггера, а весовые коэффициенты с_k определяются через интеграл [1]

(5.56)

где n - выбранное число узлов.

Как правило, в программах используют заранее вычисленные узлы и веса квадратурных формул, задаваемые в виде констант. В справочниках [36, 52] имеются достаточно подробные таблицы узлов и весов квадратурных формул Гаусса-Кристоффеля для различных видов функций (х) и разных чисел n.

Для интегралов в пределах [-, + ] при (х)=ехр (-х²) узлами квадратурной формулы (5.47) будут корни многочленов Эрмита Н_n(х), а весовые коэффициенты определяются по формуле, аналогичной (5.55), где интеграл необходимо взять в бесконечных пределах.

5.10. Методы Монте-Карло

Вычисление кратных интегралов можно осуществить повторным при­менением алгоритмов и программ, рассмотренных в предыдущих разделах. Однако с повышением кратности интегралов резко возрастает объем вычислительной работы. Методы статистических испытаний (методы Монте-Карло) свободны от этого недостатка, хотя и обеспечивают сравнительно невысокую точность. С различными вариантами методов Монте-Карло, их теоретическим обоснованием можно ознакомиться по книге [54].

Рис. 5.9. Метод Монте-Карло (вари­ант 1)

Здесь мы рассмотрим два варианта метода Монте-Карло для вычисления интегралов. Первый способ можно интерпретировать как статистический вариант метода прямоугольников (рис. 5.9), когда в качестве узла x₀ берется случайное число, равномерно распределенное на интервале интегрирования [а, b]. Вследствие случайности узла x₀ погрешность интеграла также будет носить случайный характер. Проведя N вычислений со случайными узлами x₀ усредним результат, который и принимаем за приближенное значение интеграла,

(5.56)

Погрешность интеграла будет уменьшаться с ростом числа испытаний N по закону .

Во втором варианте метода Монте-Карло интеграл приводится к виду

где 0<f(x)<1 на интервале [0, 1]. Тогда две случайные величины х_j и у_i можно рассматривать как координаты точек в единичном квадрате (рис. 5.10). При равномерном распределении точек в квадрате за приближен­ное значение интеграла принимается отношение количества точек S, попав­ших под кривую у = f(x), к общему числу испытаний N

J = S/N.

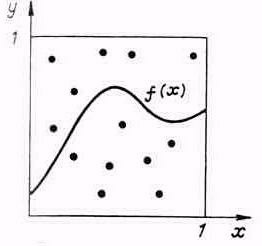
Рис. 5.10. Метод Монте-Карло (вари­ант 2)