
Мат. ан. Заочное ч.1 2часа
.pdf
Математический анализ
Введение в анализ
Часть II Функция одной переменной.
Дифференциальное исчисление

Оглавление
1.Определение функции и способы задания
2.Однозначные и многозначные функции
3.Явные и неявные функции
4.Четные и нечетные функции
5.Периодические функции
6.Монотонность
7.Ограниченность
8.Преобразование графиков функций
9.Графики основных элементарных функций
10.Обратная функция
11.Сложная функция
12.Классификация функций
13.Предел функции в бесконечности
14.Предел функции в точке
15.Свойства пределов
16.Односторонние пределы
17.Непрерывность функций
18.Бесконечно малые величины
19.Свойства б.м.
20.Бесконечно большие величины
21.Свойства б.б.
22.Связь между бесконечно большой и бесконечно малой
23.Замечательные пределы
24.Раскрытие неопределенностей

Определение функции одной переменной
Если каждому элементу множества ставится в соответствие определенный элемент множества , то на множестве задана функция = .
− независимая переменная (аргумент),− зависимая переменная (функция), буква обозначает закон соответствия,
множество − область определения функции, множество − множество значений функции.
1.Способы задания функции: 1) аналитический ( = ),
2)табличный (таблицы Брадиса),
3) графический.

2. Однозначные и многозначные функции
Если каждому значению соответствует только одно значение , то функция однозначная.
Если каждому значению соответствует несколько значений, то функция многозначная (в плане определения вообще не является функцией).
3. Явные и неявные функции
Функция называется явной, если она задана формулой, в
которой правая часть не содержит зависимой переменной.
= + 2 2 − 3
Функция аргумента называется неявной, если она задана уравнением , = 0, не разрешенным относительно
зависимой переменной.
2 + 2 = 2

4. Четные и нечетные функции
Функция , заданная на симметричном относительно начала координат промежутке, называется
1)четной, если для выполняется − = (график симметричен оси 0Y)
2)нечетной, если для выполняется − = − (график симметричен относительно начала координат)
Свойства четных и нечетных функций
Пусть |
и − четные, |
и Ψ − нечетные |
|
|
± − четная |
|
|
|
± Ψ − нечетная |
|
|
|
∙ |
− четная |
|
|
∙ Ψ |
− четная |
|
|
∙ |
− нечетная |
|

5. Периодические функции
Функция называется периодической, если существует число≠ 0 такое, что для всех из области определения функции выполняется + = .
T – период функции.
2Т, 3Т, -Т – то же периоды функции.
Главный период – наименьший из положительных периодов.
Если и − периодические функции с периодами 1 и 2,
то периодом функций ± , |
|
∙ |
, |
|
|
|
|||||
|
|||||
|
|
|
|
||
будет число Т кратное 1 и 2. |
|
|
|
|
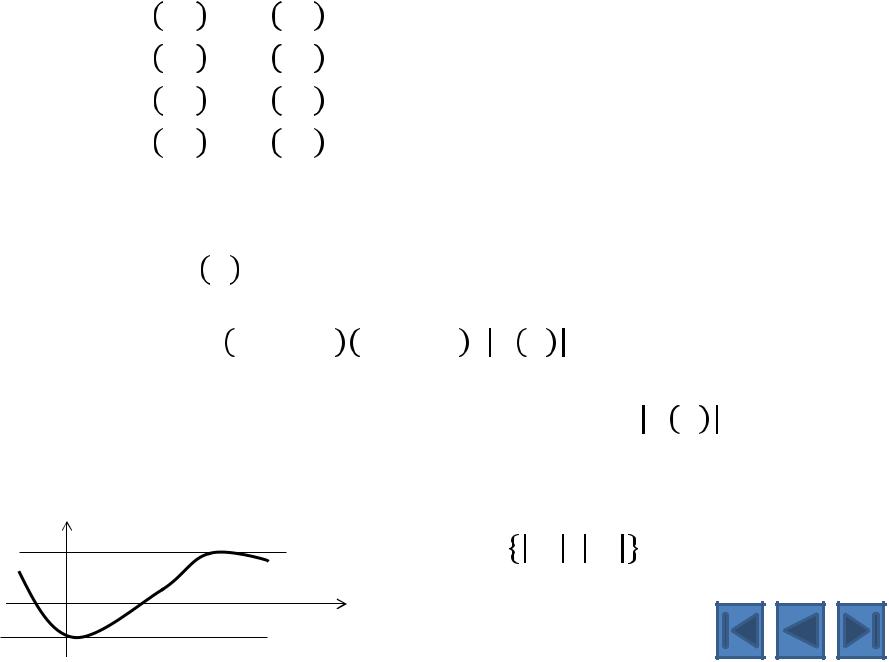
6. Монотонность на промежутке
2 |
> 1 |
|
2 |
> |
1 |
− возрастающая функция |
2 |
> 1 |
|
2 |
< |
1 |
− убывающая функция |
2 |
> 1 |
|
2 |
≥ |
1 |
− неубывающая функция |
2 |
> 1 |
|
2 |
≤ |
1 |
− невозрастающая функция |
7. Ограниченность
Функция = называется ограниченной на промежутке , если
> 0 : ≤
(существует положительное число такое, что для всех из промежутка будет выполняться неравенство ≤ )
В противном случае функция неограниченная.
|
|
|
|
= max |
, |
|
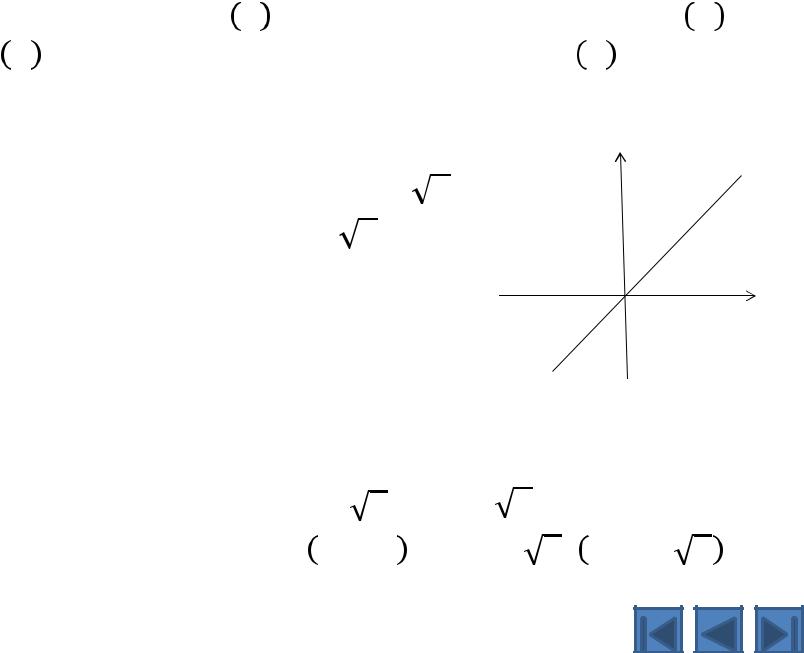
Обратная функция
Если из соотношения = вытекает соотношение = , то функция называется обратной относительно .
Обозначения переменных меняют местами и аргумент обратной
функции обозначают буквой , как и аргумент прямой функции. |
|
|||
Прямая функция = 3. |
Обратная = 3 |
|
y |
y x |
|
||||
Переобозначаем переменные = 3 . Графики прямой и обратной функции симметричны относительно прямой = .
Если обратная функция получается многозначной,
то функция необратима. Чтобы избежать этого, сужают область определения исходной функции.
x
Пример. = 2, обратная ф. = ± |
= ± |
- многозначная |
Дополняем ограничением ≥ 0 < 0 |
y = |
= − |
Для любой строго монотонной функции существует обратная
функция.
Сложная функция
Если на некотором множестве Х определена функция= с множеством значений Z,
а на множестве Z определена функция = ,
то функция = называется сложной функцией от
(или суперпозицией функций).
Классификация функций
Функция, построенная из основных элементарных функций с помощью конечного числа алгебраических действий и
конечного числа суперпозиций, называется элементарной.
= 5 2 + log2 sin 3 3 + 52 3
Примеры неэлементарных функций:
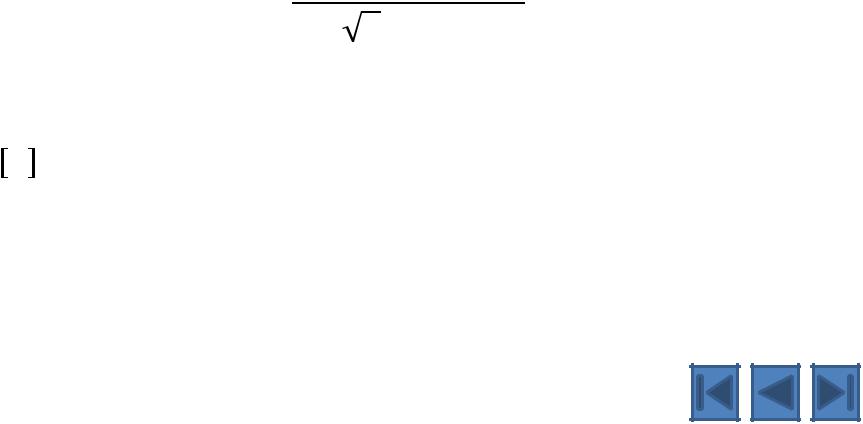
= |
- выделение целой части числа; |
|
|
= |
1, если − рациональное число |
функция Дирихле. |
|
0, если − иррациональное число |
|||
|
|
