
Мат. ан. Заочное ч.1 2часа
.pdf
Функции
неалгеброические
трансцендентные
показательные, алгебраические логарифмические,
тригонометрические, обр. тригонометрич.
целые рациональные |
дробно − |
|
иррациональные |
||
рациональные |
функции |
||||
функции |
|
|
|
|
в составе операций |
|
|
|
|||
многочлены |
|
функции |
|
|
|
|
|
|
|||
|
|
|
|
|
над аргументом есть |
|
|
|
|
|
|
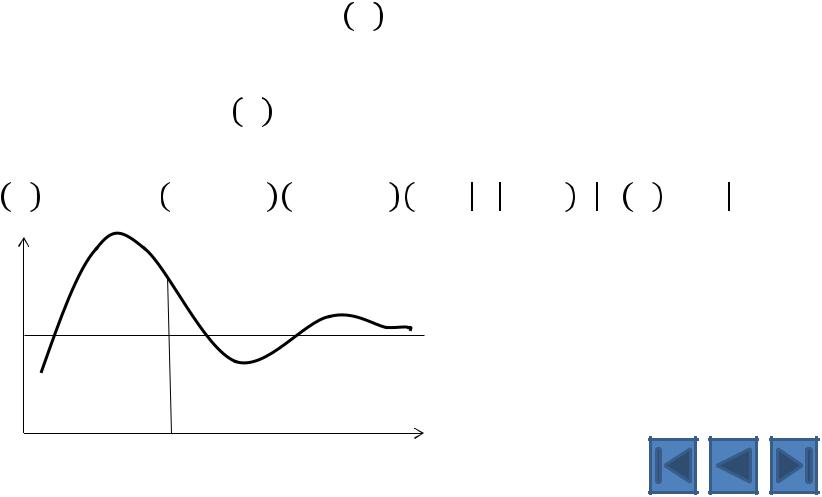
Предел функции в бесконечности
Обозначение:
|
|
|
|
lim |
= |
|
|
|
||
|
|
|
→∞ |
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ при → ∞ |
|
|
|
|||
Определение: |
|
|
|
|
|
|
|
|||
lim |
= > 0 |
> 0 |
|
: |
> : |
− |
< |
|||
→∞ |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S |
x |
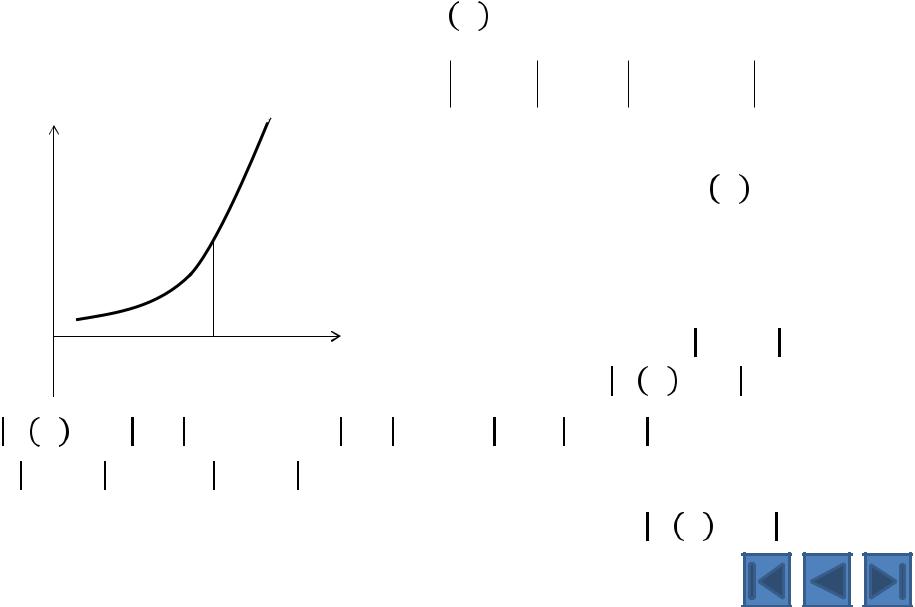
Предел функции в точке
y A
A A
|
|
|
|
|
= |
lim |
, если |
|
||
|
|
|
|
|
|
|
→0 |
|
|
|
0 0 x x , x x : f x A |
||||||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
Пример. Используя определение |
|||
|
|
|
|
|
|
|
доказать, что функция = 3 − 2 |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
в точке = 2 имеет предел равный 4. |
|||
|
|
|
|
|
|
|
Док-во: Возьмем > 0, задача |
|||
|
|
|
|
|
|
|
состоит в том, чтобы по этому найти |
|||
|
x |
|
|
|
x |
> 0, при котором из |
− 2 < |
|||
x0 |
0 |
x0 |
||||||||
|
|
|
будет следовать |
− 4 < . |
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
− 4 = 3 − 2 − 4 = 3 − 6 = 3 − 2
3 − 2 < |
− 2 < |
|
|
Значит, если взять ≤ |
3 |
|
|
, то будет выполняться |
− 4 < |
||
|
3 |
|
|

Свойства пределов
Замечание. Наличие или отсутствие предела при → 0 определяет поведение функции в окрестности точки 0, но не связано со значением функции (или его отсутствием) в самой точке 0.
Теорема. Пусть функции |
и |
имеют в точке 0 пределы, тогда |
||||||||||||||
1. |
|
lim |
|
± |
= lim |
± lim |
||||||||||
|
→0 |
|
|
|
|
|
|
→0 |
|
|
→0 |
|||||
2. |
|
lim |
|
∙ |
= |
lim |
∙ lim |
|||||||||
|
→0 |
|
|
|
|
|
|
→0 |
|
→0 |
||||||
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
3. |
|
lim |
|
= |
→ 0 |
|
|
lim ≠ 0 |
||||||||
|
|
|
lim |
|
||||||||||||
|
→0 |
|
|
|
→0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
→ 0 |
|
|
|
|
|
|
|
|
|
4. |
|
lim = |
|
|
|
|
|
|
|
|
|
|
||||
|
→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следствие: |
|
lim |
|
= lim |
|
|
|
|
||||||||
|
|
|
|
|
→0 |
|
|
→0 |
|
|
|
|
|
|||
Замечание: из lim |
|
, П, частного не следует, что пределы самих |
||||||||||||||
слагаемых, сомножителей или делимого и делителя. |
||||||||||||||||
lim |
|
∙ |
= 1 |
|
хотя |
lim |
= ∞, т.е. |
|
|
|
||||||
→ 2 |
|
|
|
|
|
|
|
|
→ 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
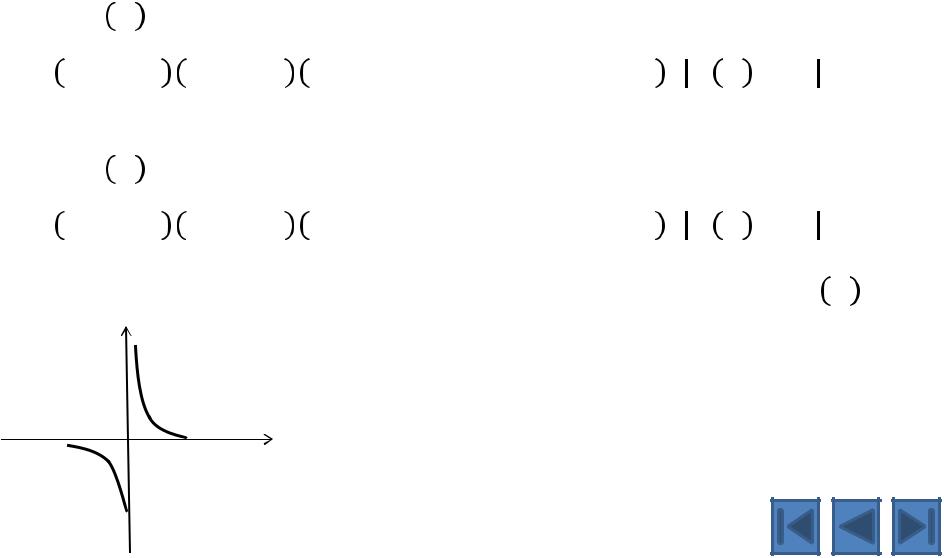
Односторонние пределы
Правый предел
lim |
= |
|
|
|
|
→ 0 |
|
|
|
|
|
> 0 > 0 ≠ 0, 0 < < 0 + : − < |
|||||
Левый предел |
|
|
|
|
|
lim |
= |
|
|
|
|
→ 0 |
|
|
|
|
|
> 0 > 0 ≠ 0, 0 − < < 0 : − < |
|||||
Пример. = 1 |
|
|
|
Теорема. Функция |
|
|
lim |
1 |
= +∞ |
имеет в точке 0 предел |
|
|
|
|
тогда и только тогда, когда |
||
|
→0 |
|
|||
|
lim |
1 |
= −∞ |
односторонние пределы |
|
|
|
|
равны и конечны. |
||
|
→0 |
|
|||

Бесконечно малые величины
Функция называется бесконечно малой (б.м.) величиной при→ 0 или при → ∞, если
lim = 0
→ 0→∞
Примеры б.м.: = sin при → 0= 5 3−7 при → ∞

Свойства б.м.
1) Алгебраическая сумма конечного числа б.м. есть б.м.
2) Произведение конечного числа б.м. есть б.м.; произведение
ограниченной функции на б.м. есть б.м. (lim( sin 1) =?)
→0
3)Частное от деления б.м. на функцию, предел которой отличен от 0, есть б.м.
lim − неопределенность
→ 0 β

Бесконечно большие величины
Функция называется бесконечно большой (б.б.) величиной при → 0 или при → ∞, если
lim = ∞
→0 →∞
Примеры б.б.: = tg при → 2
= − 6 при → ∞

Свойства б.б.
Замечание. Если функция б.б., то она неограниченная. Если функция неограниченная, то…? ( = sin ).
1)Произведение б.б. на функцию, предел которой отличен от 0, есть б.б.
lim tg ∙ |
6 + 2 = ∞ |
|
|
→2 |
|
2) Сумма б.б. и ограниченной функции есть б.б.
lim tg + sin = ∞
→2
3) Частное от деления б.б. на функцию, имеющую предел, есть б.б.
lim tg = ∞
→2 6 + 2

Связь между бесконечно большой и бесконечно малой
1. Если есть б.м. при → 0 ( → ∞), то = 1 есть б.б. при → 0 ( → ∞).
2. Если есть б.б. при → 0 ( → ∞), то = 1 есть б.м. при → 0 ( → ∞).
