
Мат. ан. Заочное ч.1 2часа
.pdf
Замечательные пределы
Первый замечательный предел
|
|
|
|
|
lim |
sin |
= 1 |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
→0 |
|
|
|||
lim |
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
→0 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin ~ |
sin ~ |
||||
lim |
5 |
|
= lim |
5 |
= lim |
5 |
= 5 |
|
||
|
|
|
|
|
||||||
→0 sin 6 |
→0 |
6 |
→0 |
6 |
|
|
6 |
|
||
|
|
|
|
|
2 |
|
2 |
|
|
|
lim |
1−cos = lim |
2 sin²2 |
= 2 lim |
2 |
= 2 lim |
= 2 lim |
1 |
= 1 |
||
2 |
2 |
4 2 |
|
|||||||
→0 |
2 |
→0 |
→0 |
→0 |
→0 |
4 |
2 |
|||

Второй замечательный предел |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
lim |
1 + |
1 |
|
= |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
= |
|
|
|
, |
|
= |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
При → ∞, |
→ 0 |
lim |
1 + |
= |
|
|
|
|
|
||||||||||
|
|
|
→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
1 + |
= |
|
lim |
|
|
1 + |
|
|
|
= |
||||||||
|
|
|
|
|
|
|
|
||||||||||||
→∞ |
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||
|
|
lim 1 + |
|
|
|
|
|
|
|
|
|||||||||
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
lim 1 + |
|
= |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Дифференциальное исчисление Оглавление
1. |
Производная |
18. Раскрытие неопределенностей с |
2. |
Геометрический смысл производной |
помощью правила Лопиталя |
3.Физический смысл производной
4.Правая и левая производные
5.Правила дифференцирования
6.Производная сложной функции
7.Производная обратной функции
8.Производные основных элементарных функций
9.Производная неявной функции
10.Производные высших порядков
11.Формула Лейбница для производной произведения двух функций
12.Основные теоремы дифференциального исчисления
13.Теорема Ферма
14.Теорема Ролля
15.Теорема Лагранжа
16.Теорема Коши
17. Правило Лопиталя
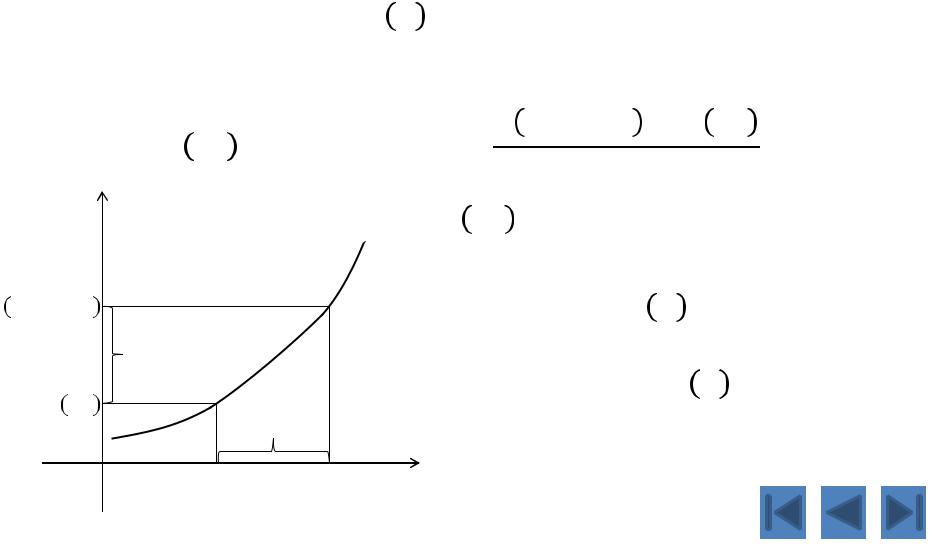
Дифференциальное исчисление Производная
Производной функции = в точке 0 называется предел при ∆ → 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).
|
′ 0 |
= lim |
∆ |
= lim |
0 + ∆ − 0 |
|||||||||
|
∆ |
|
∆ |
|||||||||||
|
|
∆ →0 |
|
|
∆ →0 |
|
||||||||
|
|
|
|
|
|
′ |
|
= lim ∆ = ∞ -бесконечная |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
∆ →0 ∆ |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
производная в точке 0. |
||||||||
0 + ∆ |
|
|
|
|
|
Если функция имеет конечную |
||||||||
|
∆ |
|
|
|
|
производную в каждой точке , |
||||||||
0 |
|
|
|
|
|
то производную ′ можно |
||||||||
|
∆ |
|
|
|
рассматривать как функцию от на |
|||||||||
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
промежутке Х. |
||||||||
0 |
0 + ∆ |
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
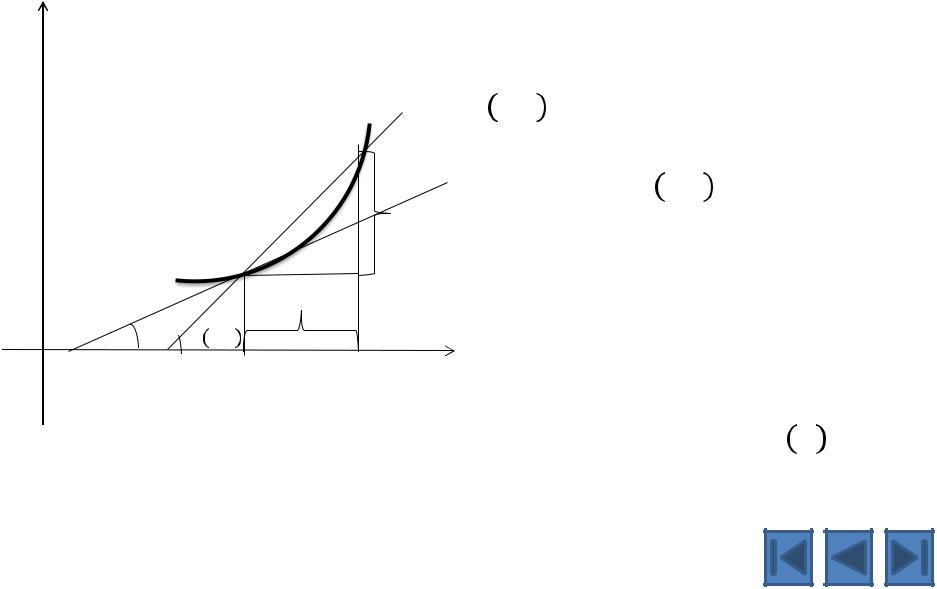
Геометрический смысл производной
M
|
∆ |
0 |
0 |
1
∆
N
∆
0 + ∆
MM - секущая
∆ - угол между секущей и осью Ох.
Если lim ∆ = , то
∆ →0
прямую с угловым коэффициентом = ,
проходящую через точку М(х ;f(x )), называют предельным
положением секущей ММ при ∆х → 0 или касательной к графику функции = в точке М.

Можно доказать, что если = имеет в точке 0 производную, то существует касательная к графику функции в
точке 0; 0 |
, причем = ′ 0 . |
Физический смысл производной
Понятие скорости, заимствованное из физики, удобно при исследовании поведения произвольной функции.
Какую бы зависимость не отражала функция = ,
отношение ∆ есть средняя скорость изменения
∆
относительно изменения , а ′ 0 – мгновенная скорость изменения при = 0.
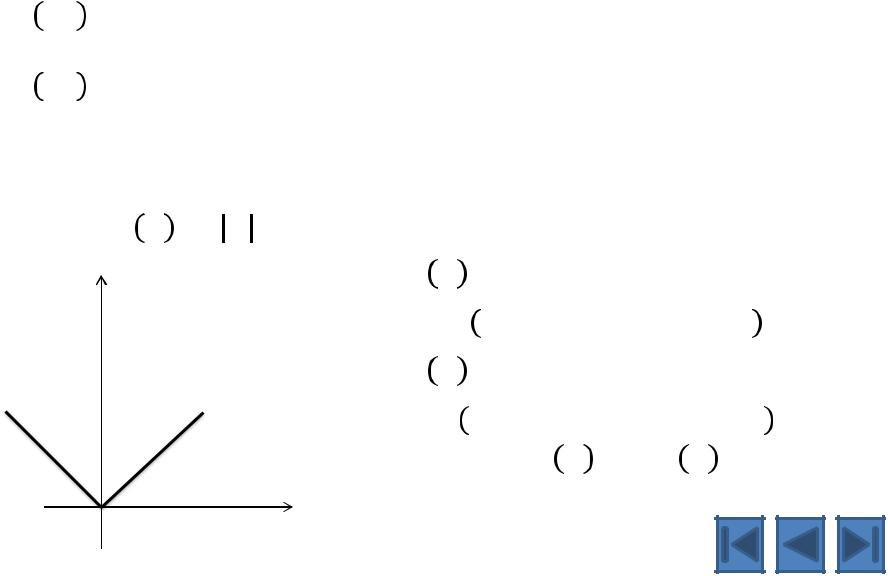
Правая и левая производные
′ |
= |
lim ∆ |
- правая производная |
0 |
|
∆ →0 ∆ |
|
|
|
|
|
′ |
= |
lim ∆ |
- левая производная |
0 |
|
∆ →0 ∆ |
|
|
|
|
Если функция имеет в точке производную, то она имеет в этой точке правую и левую производные, которые совпадают.
Пример.
0
= , точка 0 = 0
′ 0 = lim ∆ = 1
∆ →0 ∆
при ≥ 0 ∆ = ∆
′ 0 = lim ∆ = −1
∆ →0 ∆
при < 0 ∆ = −∆′ 0 ≠ ′ 0
Функция не имеет в точке 0 производной.
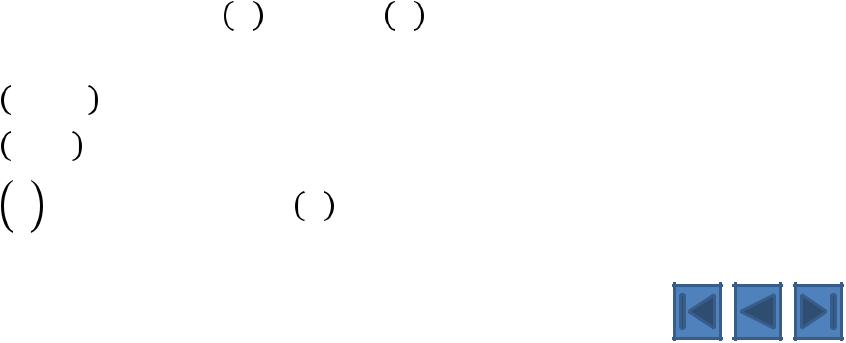
Замечание. Для функции одной переменной дифференцируемость и существование производной – понятия равносильные.
Поэтому операцию нахождения производной часто называют дифференцированием.
Правила дифференцирования
Если функции u= |
и = дифференцируемы в |
точке 0, то |
|
1.± ′ = ′ ± ‘
2.∙ ′ = ′ + ‘
3. |
|
′ = |
′ − ′ |
при ( ≠ 0) |
|
2 |

Производная сложной функции
Теорема. Если = и = −дифференцируемые функции от своих аргументов, то производная сложной функции = существует и равна производной данной функции по промежуточному аргументу u, умноженной на производную самого промежуточного
аргумента по независимой переменной x, т.е.
′ = ′ ∙ ‘
= ∙ − другая форма записи правила дифференцир.
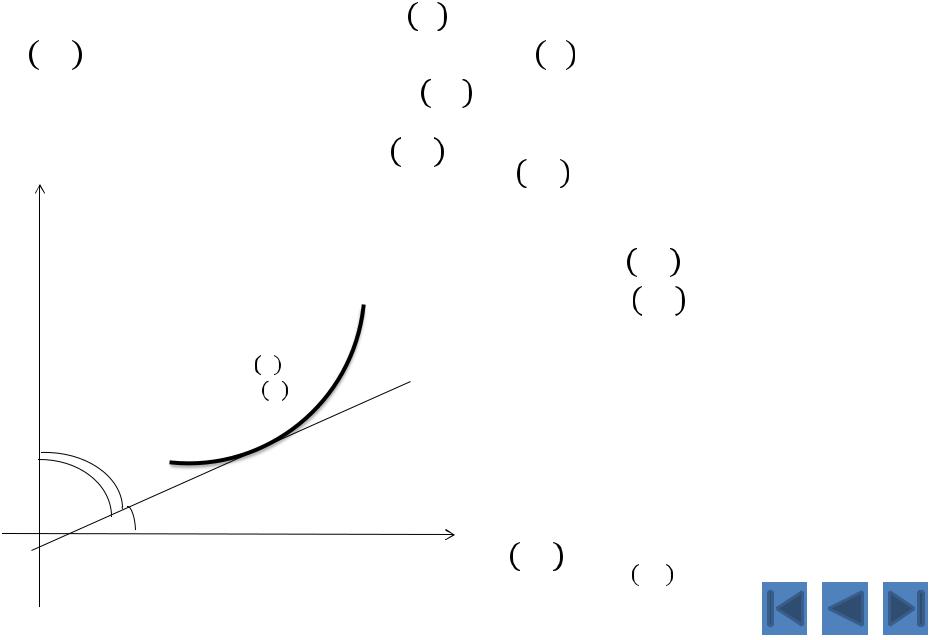
Производная обратной функции
Теорема. Если функция = имеет в точке 0 производную
′ 0 |
≠ 0, то обратная функция = |
также имеет в |
|
|
|
|
|
||||||||||
соответствующей точке = производную, причем |
|
|
|
|
|
||||||||||||
|
|
′ 0 |
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
′ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Геометрический смысл формулы |
|||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
′ |
|
= |
|
|
|
|
|
|||
|
|
|
|
|
|
|
′ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= tgβ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
= или |
+ = |
|
(если и острые углы) |
||||||||||||
|
|
= |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 (если и тупые углы) |
|||||||||||||
|
|
|
+ = |
||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда tgβ = ctgα или tgβ = |
1 |
|
|
|
||||||||||
|
|
|
tgα |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
′ 0 |
= |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
′ 0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
