
Мат. ан. Заочное ч.1 2часа
.pdf
Теорема Лагранжа. . Пусть на , определена функция , причем:
1) |
|
|
непрерывна на , |
2) |
|
|
дифференцируема на , |
Тогда существует по крайней мере одна точка |
, ,в которой |
|
′ |
= − . |
|
|
− |
|
Замечание. |
|
− = ′ − , |
< < |
формула Лагранжа или формула конечных приращений.

|
1 |
0 |
|
|
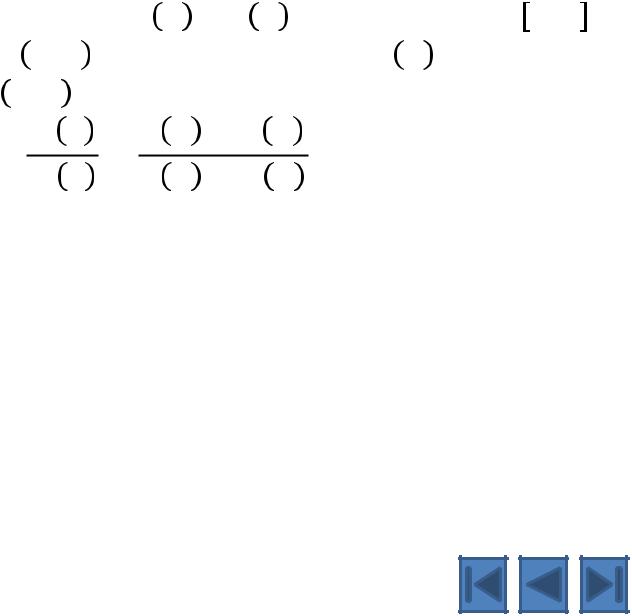
Геометрический смысл теоремы
Лагранжа:
−
−
−угловой коэффициент секущей ММ ′ - угловой коэффициент касательной
Существует точка с такая, что касательная к графику в точке ; параллельна секущей
ММ
Теорема Коши. Пусть функции и |
непрерывны на , и |
|
дифференцируемы на |
, . Пусть, кроме того, ′ ≠ 0 . Тогда |
|
существует точка |
, такая, что |
|
′ − ′ = −
Формула Коши или обобщенная формула конечных приращений.

Правило Лопиталя
Теорема Лопиталя. Пусть функции и определены и дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой точки а (или при → ∞). Пусть
lim = |
lim = 0 ∞ |
→ ∞ |
→ ∞ |
в указанной окрестности точки а (или при → ∞). Тогда, если существует предел отношения производных
lim |
′ |
конечный или бесконечный , то |
|
′ |
|||
→ ∞ |
|
lim |
|
= |
lim |
′ |
|
|
|||
→ ∞ |
|
→ ∞ ′ |
||
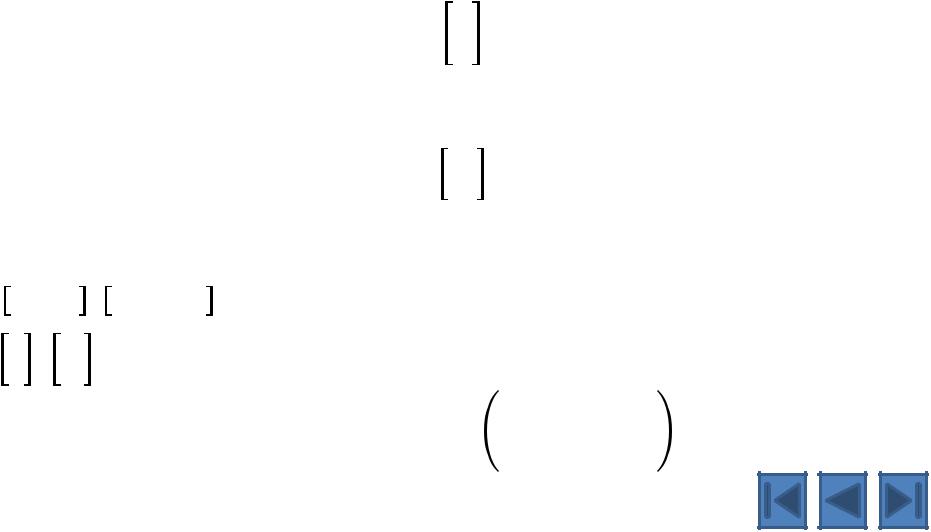
Раскрытие неопределенностей с помощью правила Лопиталя
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
1 − cos |
; |
lim |
0− sin |
; |
lim |
− 1 |
||||||||
2 |
|
|
∞ 3 |
|
|
||||||||||
→0 |
|
|
→0 |
|
|
|
|
→0 |
|||||||
|
|
|
|
ln |
|
|
∞ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
lim |
; |
|
lim |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
→∞ |
|
|
|
|
→+∞ |
|
|
||||||
0 ∙ ∞ , ∞ − ∞ алгеброическими преобразованиями сводим к
0 |
, |
∞ |
0 |
|
∞ |
lim ln ; lim |
1 |
− |
||
cos |
||||
|
→2 |
|
||
→0 |
|
|
|
|
|
|
|
||

00 , 1∞ , ∞0 с помощью основного логарифмического
тождества сводятся к неопределенности 0 ∙ ∞
|
= ln |
= |
ln |
= 0∙∞ |
|
lim ; |
lim 1 + 2 |
1 |
|
lim 2 cos |
|
−1− |
; |
||||
→0 |
→0 |
|
|
|
|
|
|
→2 |
|
||
|
|
|
|
|
|
