
Конспект_лекций3
.pdfНаціональний технічний університет України «Київський політехнічний інститут»
В. О. Гайдей, Л. Б. Федорова І. В. Алєксєєва, О. О. Диховичний
РЯДИ. ФУНКЦІЇ КОМПЛЕКСНОЇ ЗМІННОЇ. ОПЕРАЦІЙНЕ ЧИСЛЕННЯ
КОНСПЕКТ ЛЕКЦІЙ
Київ — 2013
Диференціальне та інтегральне числення функцій однієї змінної. Конспект лекцій. (ІІ курс І семестр) / Уклад.: В. О. Гайдей, Л. Б. Федорова, І. В. Алєксєєва, О. О. Диховичний. — К: НТУУ «КПІ», 2013. — 108 с.
Навчальне видання
Ряди.
Функції комплексної змінної. Операційне числення Конспект лекцій
для студентів ІІ курсу технічних спеціальностей
Укладачі: Гайдей Віктор Олександрович, канд. фіз-мат. наук, доц. Федорова Лідія Борисівна, канд. фіз-мат. наук, доц. Алєксєєва Ірина Віталіївна, канд. фіз-мат. наук, доц.
Диховичний Олександр Олександрович, канд. фіз-мат. наук, доц.
ЗМІСТ
Передмова ................................................................................................................. |
4 |
Розділ 1. Ряди |
|
Лекція 1. Числові ряди ............................................................................................ |
5 |
Лекція 2. Ознаки збіжності рядів з невід’ємними членами .............................. |
12 |
Лекція 3. Числові ряди з довільними членами .................................................. |
17 |
Лекція 4. Функціональні ряди.............................................................................. |
22 |
Лекція 5. Степеневі ряди....................................................................................... |
25 |
Лекція 6. Тейлорів ряд........................................................................................... |
29 |
Лекція 7. Ряди Фур’є. Ч. 1 ...................................................................................... |
36 |
Лекція 8. Ряд Фур’є. Ч. 2........................................................................................ |
44 |
Розділ 2. Теорія функцій комплексної змінної |
|
Лекція 9. Функції комплексної змінної ............................................................... |
53 |
Лекція 10. Диференціювання функцій комплексної змінної............................ |
62 |
Лекція 11. Інтегрування функцій комплексної змінної .................................... |
68 |
Лекція 12. Ряди Тейлора і Лорана........................................................................ |
75 |
Лекція 13. Ізольовані особливі точки...................................................................... |
80 |
Лекція 14. Основна теорема про лишки та її застосування............................... |
86 |
Розділ 3. Операційне числення |
|
Лекція 15. Перетворення Фур’є ............................................................................ |
89 |
Лекція 16. Перетворення Лапласа. Операційне числення ............................... |
94 |
Лекція 17. Застосування операційного числення............................................. |
103 |
ПЕРЕДМОВА
Конспект лекцій з вищої математики «Ряди. Функції комплексної змінної. Операційне числення» є складовою навчального комплекту
звищої математики, який містить:
—конспект лекцій,
—практикум,
—збірник індивідуальних домашніх завдань,
—збірник контрольних та тестових завдань.
Конспект складено на основі багаторічного досвіду викладання математики в НТУУ «Київський політехнічний інститут», його зміст відповідає навчальним програмам з вищої математики всіх технічних спеціальностей НТУУ «КПІ» денної та заочної форм навчання і містить такі розділи дисципліни «Вища математика»:
—числові і функціональні ряди;
—теорія функцій комплексної змінної;
—інтегральні перетворення Фур’є і Лапласа та їх застосування. Конспект містить теоретичний матеріал, обсяг і рівень строгості
якого потребує курс вищої математики для майбутніх інженерів. Передбачено, що опанування лекції з конспекту супроводжується опануванням відповідного заняття з практикуму.
Метою конспекту є:
—систематичний виклад теоретичного матеріалу, що звільняє лектора від «надиктовування» і дозволяє більше пояснювати;
—ефективна підготовка студента до колоквіуму та іспиту;
—виділення наріжних питань математичного аналізу.
Пропонований конспект супроводжує, але аж ніяк не замінює живу лекцію, як і текст драматичного твору не замінює вистави.
РОЗДІЛ 1. РЯДИ
ЛЕКЦІЯ 1. ЧИСЛОВІ РЯДИ
1.1. Основні поняття
Розгляньмо числову послідовність
{an } {a1,a2, ...,an, ...}.
Вираз
an a1 a2 ... an ...
n 1
називають числовим рядом (рядом). Числа a1,a2,... називають членами
ряду, а an f (n) — n -м (загальним) членом ряду.
Для скорочення замість an інколи писатимемо an .
n 1
Уточнимо, як розуміють «додавання» нескінченної кількості членів ряду.
Суму перших n членів ряду називають n -ю частковою сумою ряду і позначають
|
|
n |
|
|
Sn a1 a2 ... an ak . |
|
|
|
k 1 |
|
|
Ряд |
|
|
|
|
|
|
|
|
Rn an 1 an 2 ... |
ak , |
|
|
|
k n 1 |
|
який одержують відкиданням з ряду an його перших n членів, нази-
вають n -м залишком ряду.
Приміром, |
|
|
|
|
||
1 |
1 |
1 |
1 |
... |
1 |
... — ряд, який називають гармонічним, |
|
2 |
3 |
4 |
|
n |
|
a |
1 |
— загальний член ряду, |
||||
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
Розділ 1. Ряди |
Sn n 1 — n -скінченна сума,
k 1 k
|
|
1 |
|
Rn |
|
— n -й залишок ряду. |
|
|
k n 1 |
k |
|
|
|
|
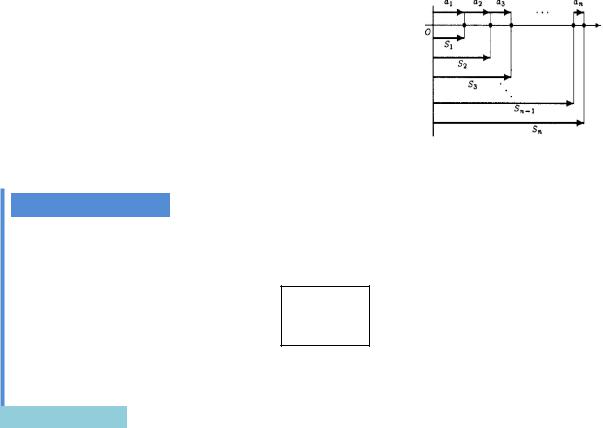
Розгляньмо послідовність {Sn } часткових сум ряду:
S1 a1,
S2 a1 a2,
S3 a1 a2 a3,
...............................,
Sn a1 a2 ... an,
......................................... Рис. 1.1. Часткові суми ряду з додатними членами
Означення 1.1 (суми ряду). Якщо послідовність часткових сум {Sn } збігається до числа S, то ряд an називають збіжним, а число
S lim Sn називають сумою ряду і пишуть
n
S an .
n 1
Якщо послідовність {Sn } скінченної границі не має, то ряд an на-
зивають розбіжним.
Приклад 1.1. Дослідити на збіжність ряди:
1) 0 0 ... 0 ...; 2) 1 1 ... 1 ...;
3) 1 1 1 1 ... 1 1 ....
Зауважимо, що існує аналогія між поняттями невластивого інтеграла і ряду:
1
|
|
A |
f (x)dx |
lim |
f (x)dx; |
|
A 1 |
|
|
n |
|
an |
lim |
ak . |
n 1 |
n k 1 |
|
Прикладом збіжного числового ряду є дійсне число, яке можна записати як нескінченний десятковий дріб:
a |
,a a |
...a ... a |
0 |
|
a1 |
|
a2 |
... |
an |
... |
|
|
|
||||||||
0 |
1 2 |
n |
10 |
102 |
10n |
|
||||
|
|
|
|
|
||||||
Лекція 1. Числові ряди |
7 |
1.2. Важливі приклади рядів
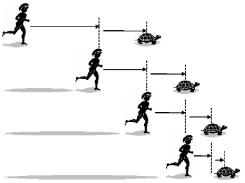
1.2.1. Парадокс про Ахіллеса і черепаху
Розгляньмо сучасний варіант парадоксу, запропонованого, давньогрецьким філософом Зеноном:
«Прудкий Ахіллес ніколи не наздожене черепаху, якщо перед початком руху черепаха буде попереду на деякій віддалі від нього».
Припустімо, що Ахіллес бігає у десять разів швидше за черепаху, і перебуває на віддалі в 1000 метрів від черепахи. За той час, за який Ахіллес пробіжить ці 1000 метрів, черепаха проповзе 100 метрів. Коли Ахіллес пробіжить 100 метрів, черепаха проповзе ще 10 метрів тощо. Процес триватиме до нескінченності. Ахіллес так ніколи не наздожене черепаху?
1.2.2. Геометричний ряд
Дослідімо збіжність ряду
a aq aq2 ... aqn 1 ...
Рис. 1.2. Чи наздожене Ахіллес черепаху?
aqn 1,a 0,
n 1
який називають геометричним рядом. {aqn 1} — геометрична прогресія. Часткова сума геометричного ряду
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
a aq |
|
|
|
a |
|
|
aq |
|
q 1, |
||||
|
|
|
|
|
|
|
, |
||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 q |
|
1 |
q |
1 |
q |
|||||||||
n |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
na, |
|
|
|
|
|
|
q 1. |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розгляньмо можливі випадки: |
|
|
|
|
|
|
|
|
||||||||
1) |
якщо |
|
q |
|
1, |
то |
lim qn 0 і |
|
lim S |
n |
|
|
|
|
a |
; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
q |
|||||||||||
|
|
|
|
|
|
|
n |
n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
якщо |
|
q |
|
1, |
то |
lim qn і |
lim S |
n |
; |
|
|||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
якщо q 1, то ряд набуває вигляду |
|
|
|||||||||||||
|
|
|
|
|
|
|
a a a a ... , |
|
|
|||||||
S2k 0,S2k 1 a і |
lim Sn не існує; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|

8 |
Розділ 1. Ряди |
4) якщо q 1, |
|
то lim Sn |
lim (na) . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
q |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
aq |
|
|
|
|
|
|
|
|
|
|
|
1 q |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
розбігається, |
|
|
q |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Оскільки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1000 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1000 |
|
|
|
10000 1111,(1), |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.3. Сума геометричного |
|||||||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ряду |
|
|||||||
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
то Ахіллес наздожене черепаху, пробігши |
1 |
|
|
1 |
1 |
|
||||||||||||||||||||||||||||||||||||
1111,(1) метра. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
... 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
2n |
|||||||||||||||
1.2.3. Гармонічний ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Дослідімо збіжність гармонічного ряду |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
... |
... |
|
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
n |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
n |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кожен член ряду, починаючи з другого є середнім гармонічним двох сусідніх:
|
|
|
an |
|
2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
a |
a |
|
|
|||
|
|
|
|
|
|
|
|
||||
Оскільки |
|
|
|
|
n 1 |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
dx dx |
1 |
|
|||
|
|
k : |
, |
||||||||
|
|
|
|
|
k |
x |
|
|
|
k |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
k 1 |
dxx |
|
|
|
|
|
|
|
Sn k1 |
|
|
|
|
|
|
|
||||
k 1 |
k 1 |
k |
|
|
|
|
|
|
|
|
|
n1
1 dxx ln x |n1 1 ln(n 1).
Отже,
n : Sn |
ln(n 1) lim Sn |
. |
|
n |
Рис. 1.5. Гармонічний ряд |
Гармонічний ряд розбіжний. |
||

|
Лекція 1. Числові ряди |
9 |
1.2.4. Телескопічний ряд |
|
|
Дослідімо збіжність ряду |
|
|
|
|
|
an |
a1 a2 ... an ... (bn bn 1) |
|
n 1 |
k 1 |
|
(b1 b2) (b2 b3) ... (bn bn 1) ..., |
||
який називають телескопічним. |
|
|
Оскільки |
|
|
n |
n |
|
Sn ak |
(bk bk 1) |
Рис. 1.6. Телескопічні ряди |
k 1 |
k 1 |
|
(b1 b2 ) (b2 b3 ) ... (bn bn 1) b1 bn 1,
то послідовність {Sn } збігається, якщо збігається послідовність {bn }.
Приклад 1.2. Дослідити збіжність ряду:
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
1) |
|
|
; 2) |
|
ln 1 |
|
|
. |
|
|
|
|
n 1 n(n 1) |
n 1 |
|
|
n |
|
|
|
|||
1.3. Основні властивості рядів |
|
||||||||||
Сумою (різницею) рядів |
an |
та bn називають ряд |
(an bn ) (ряд |
||||||||
(an bn )).
Властивість 1 (дистрибутивність збіжного ряду). Якщо ряди із загальними членами an та bn збігаються відповідно до сум S та T,
то ряд із загальними |
членом |
cn an bn |
збігається до суми |
||||||||||||||||
S T : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( an bn ) an bn S T. |
|
|||||||||||||||||
Справді, |
n 1 |
|
|
|
|
|
|
|
n 1 |
|
n 1 |
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
lim |
|
|
( a |
k |
|
k |
|
|
|
a |
k |
|
k |
|
|
||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
b ) |
lim |
|
|
b |
|
|
|
|||||||
|
|
n |
k 1 |
|
|
|
|
|
n |
k 1 |
|
|
|
k 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
lim |
ak |
lim |
bk |
S T. |
|
|
|
||||||||||
|
|
|
n k 1 |
|
|
n k 1 |
|
|
|
|
|
|
|
|
|||||
|
|
Що можна сказати про ряд ( an ), |
|
|
якщо ряд an |
||||||||||||||
Питання 1.1. |
|
|
0, |
||||||||||||||||
розбігається? |
|
Що можна сказати про ряд (an bn ), якщо ряд an збі- |
|||||||||||||||||
Питання 1.2. |
|
||||||||||||||||||
гається, а ряд bn — розбігається?

10 |
Розділ 1. Ряди |
Властивість 2. Якщо переставити, відкинути або дописати скінченну кількість членів ряду, то це не вплине на його збіжність (розбіжність).
Вказані дії змінюють на одну й ту саму скінченну величину всі часткові суми, починаючи з деякого номера, а це не впливає на збіжність або розбіжність послідовності скінченних сум ряду.
Зауважимо, що після вказаних дій сума ряду може змінитись.
Властивість 3 (асоціативність збіжного ряду). Якщо ряд збі-
гається, то його члени можна групувати будь-яким чином, не переставляючи їх.
Зауваження.
1. Розкривати дужки, взагалі кажучи, не можна: так ряд
(1 1) (1 1) (1 1) ... 0 0 0 ...
збіжний, а ряд
1 1 1 1 1 1 ...
розбіжний.
2.Переставляти члени ряду, взагалі кажучи, не можна.
3.У збіжному ряді можна розставляти дужки, але не можна їх розкривати.
Властивість 4. Числовий ряд збігається тоді й лише тоді, коли збігається будь-який його залишок.
Якщо ряд an збігається, то
lim ak 0.
n k n 1
1.4. Необхідна ознака збіжності ряду
Теорема 1.1 (необхідна ознака збіжності ряду). Якщо ряд
an збігається, то lim an |
0. |
|
|
|
|||||
|
n |
|
|
|
|
|
|
||
Якщо S — сума заданого ряду, то |
|
|
|||||||
|
lim S |
|
lim (S |
|
a |
) S; lim S |
S. |
||
|
n |
n |
|
n |
n 1 |
n |
n n 1 |
|
|
Отже, |
|
|
|
|
|
|
|
|
|
|
lim an |
lim (Sn Sn 1) S S 0. |
|||||||
|
n |
|
|
n |
|
|
|
||
|
(достатня |
умова |
розбіжності ряду). Якщо |
||||||
Наслідок |
|||||||||
lim an 0, то |
ряд an |
розбігається. |
|
||||||
n |
|
|
|
|
|
|
|
|
|
