
Конспект_лекций3
.pdf
Лекція 8. Ряд Фур’є. Ч. 2 |
51 |
A0 An sin( nx n ),
n 1
яку називають гармонічною.
Складна T -періодична функція f(x) повністю визначається сукупністю амплітуд An , n 0, 1, 2, ..., та початкових фаз n , n .
Сукупність A0 , A1, A2, ..., An, ... називають дійсним амплітудним частотним спектром періодичної функції f (x).
Сукупність 1, 2, ..., n , ... називають фазовим частотним спектром періодичної функції f (x).
Амплітудний спектр зображують точками ( A0 ; 0), (An ; 1n), n ,
які унаочнюють вертикальними відрізками. Амплітудний спектр періодичної
функції f(x) дискретний (лінійчатий). Оскільки частоти гармонік кратні основній частоті 1, то спектр склада-
ється з рівновіддалених спектральних
ліній. |
Рис. 8.8. Амплітудний спектр |
|
періодичної функції |
Розглядають також і комплексні спектри: сукупність
Cn cn , n ,
називають амплітудним спектром функції f ;
сукупність
n arg cn , n ,
називають фазовим спектром функції f (x) (зазвичай тут вважають,
що arg z ( ; ]).
Приклад 8.4. Знайти амплітудний і фазовий спектри ряду Фур’є фу-
|
|
|
x |
|
1, |
||||
|
|
|
|||||||
1, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
нкції f (x) |
0, |
1 |
|
x |
|
2. |
|||
|
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
Розділ 1. Ряди |

РОЗДІЛ 2. ФУНКЦІЇ КОМПЛЕКСНОЇ ЗМІННОЇ
ЛЕКЦІЯ 9. ФУНКЦІЇ КОМПЛЕКСНОЇ ЗМІННОЇ
9.1. Множини на комплексній площині
1. Комплексна площина. Комплексне чи-
сло z x iy зображають на площині Oxy точ-
кою M(x;y) або її радіусом-вектором OM. Це встановлює взаємну однозначну відповідність між множиною комплексних чисел і множи-
ною точок площини 2. Площину, на якій зображають комплексні числа, називають комплексною площиною і позначають .
Віддаль між двома точками z1 x1 iy1 та z2
ної площини визначають за формулою
y z
y |
M z x iy |
O |
x x |
Рис. 9.1. Комплексна площина
x2 iy2 комплекс-
|
|
|
|
(z ,z |
) |
|
z |
2 |
z |
1 |
|
(x |
2 |
x |
)2 |
(y |
2 |
y )2 . |
|
|
|||||||
|
|
|
|
||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|||||||||
2. Окіл. -околом точки |
|
z0 |
називають |
y |
|
z |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
множину точок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
U (z0 ) z | |
|
z z0 |
|
. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
z0 |
x0 iy0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-окіл точки z0 |
є відкритим кругом із центром |
||||||||||||||||||||||||||
O |
|
x |
|||||||||||||||||||||||||
у точці z0 радіусом : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.2. -окіл на |
|||||||||||
|
z z0 |
|
(x x0)2 (y y0)2 2. |
|
|
|
комплексній |
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
площині |
||||||||||||||||||||||

54 |
Розділ 2. Функції комплексної змінної |
3. Відкрита множина. Точку M0 D називають внутрішньою
точкою множини D, якщо вона належить множині D разом з деяким своїм -околом. МножинуD називають відкритою, якщо кожна її точка внутрішня.
Прикладом відкритої множини є -окіл будь-якої точки.
4. Область. Множину D називають зв’язною, якщо будь-які дві її точки можна з’єднати неперервною кривою (зокрема ламаною), що повністю лежить у множині D.
Відкриту зв’язну множину називають областю.
L
D D  D
D D
D
Рис. 9.4. Приклади незв’язних множин
Рис. 9.3. Приклади зв’язних множин
5.Межа множини. Точку M називають межовою точкою множини D, якщо будь-який її окіл містить як точки, які належать D, так
іточки, які їй не належать. Множину всіх межових точок множини називають межею множини D і позначають D.
6.Однозв’язна область. Замкнену криву без самоперетинів називають контуром. Будь-який контур розбиває площину на дві різні області і є межею кожного з них. Одна з областей — внутрішність контуру — обмежена, а інша — зовнішність контуру — необмежена.
Область D називають однозв’язною, якщо внутрішність будь-якого контуру, що належить D, також належить D.
7.Замкнена множина. Точку M називають граничною точкою множини D, якщо кожен її окіл містить нескінченну кількість точок
множини D.
Кожна гранична точка множини є або її внутрішньою точкою, або її межовою точкою. Об’єднання множини D і множини її граничних точок називають замиканням множини D і позначають D.
Множину D називають замкненою, якщо вона містить усі свої граничні точки, тобто збігається з власним замиканням.
Прикладом замкненої множини є круг зі своєю межею колом.
8. Окіл нескінченно віддаленої точки. Розгляньмо послідов-
ність {zn } комплексних чисел z1, z2, ..., zn, ...
Якщо для будь-якого числа M 0 існує натуральне число N таке, що всі члени zn послідовності {zn } з номерами n N справджують
нерівність
zn M,
то вважають, що послідовність {zn } збігається до нескінченно віддаленої точки, до нескінченності, і пишуть
lim zn .
n

Лекція 9. Функції комплексної змінної |
55 |
Поповнюючи площину комплексної змінної так запровадженою нескінченно віддаленою точкою z , дістають розширену комплексну площину.
Околом нескінченно віддаленої точки (R — околом) називають сукупність усіх точок z, які справджують нерівність z R (з приєд-
наною нескінченно віддаленою точкою), тобто сукупність усіх точок z, які лежать за межами круга досить великого радіуса R з центром у початку координат.
9.Криві на комплексній площині. Нехай
xx(t),y y(t),t T,
—неперервні або неперервно диференційовні дійсні функції. Тоді
комплексна функція
z(t) x(t) iy(t),t T,
означує на комплексній площині неперервну чи гладку криву L, яку на площині Oxy задають параметричні рівняння
|
|
x x(t), |
|
|
t T. |
|
|
y y(t), |
|
|
|
|
|
Приклад 9.1. Записати в комплексній формі рівняння кола з центром у точці z0 x0 iy0 радіусом R.
9.2.Функції комплексної змінної
1.Означення функції комплексної змінної. Нехай задано дві множини D та E, елементами яких є комплексні числа
|
z x iy |
D, |
|
|
|
|
|
|
w u iv |
E. |
|
|
|
|
|
Якщо |
кожному числу z D за |
деяким |
y |
Cz |
v |
Cw |
|
правилом |
f поставлено у відповідність певне |
|
|
|
|||
D |
|
E |
|||||
число w E, то кажуть, що на множині D |
f |
||||||
z |
|
w |
|||||
означено |
однозначну функцію комплексної |
|
|
|
|
||
змінної |
|
|
O |
x |
O |
u |
|
|
w f (z) |
|
Рис. 9.5. Функція |
||||
що відображує множину D у множину E. |
комплексної змінної |
||||||
Якщо кожному z D відповідає декілька значень w, |
то функцію |
||||||
w f (z) називають багатозначною. |
|
|
|
|
|
||
Функція w f (z) перетворює комплексні числа z |
x iy |
на ком- |
|||||
плексні числа w u iv : |
|
|
|
|
|
||
|
f (z) f (x iy) u(x, y) iv(x, y). |
|
|
|
|||

56 |
Розділ 2. Функції комплексної змінної |
Отже, комплекснозначну функцію комплексної змінної z x iy
можна розглядати як пару дійсних функцій
u u(x, y), v v(x, y),
двох дійсних змінних x та y. |
називають |
|
|
функції |
|||
|
Функцію |
u(x, y) Re w |
дійсною |
частиною |
|||
w f (z), а функцію v(x, y) Im w — її уявною частиною. |
|
||||||
|
|
|
Знайти |
дійсну |
та уявну |
частини |
функції |
|
Приклад |
9.2. |
|||||
w z2 3z 2.
9.3. Границя і неперервність функції комплексної змінної
1. Границя функції. Нехай функція w f (z) означена в деякому
проколеному околі U (z0 ) \ {z0} точки z0 |
x0 iy0. |
|
|
Число |
A a bi називають границею функції |
f (z) у точці z0, |
|
якщо для |
будь-якого 0 існує |
0, таке, |
що для всіх |
z U (z0) \ {z0} виконано нерівність
f(z) A
і пишуть
A lim f (z).
z z0
Зауважимо, що функція w f (z) прямує до своєї границі A неза-
лежно від способу наближення точки z до точки z0.
Існування границі
lim f (z) A a ib
z z0
рівносильно існуванню границі двох дійсних функцій u(x, y) та v(x, y): lim u(x, y) a, lim v(x, y) b.
x x0 |
x x0 |
y y0 |
y y0 |
2. Властивості функцій, що мають скінченні границі.
1.Якщо f (z) має в точці z0 границю, то ця границя єдина.
2.Функція f (z), яка має границю в точці z0, обмежена в деякому
проколеному околі цієї точки:
C 0 z D : f (z) C.

Лекція 9. Функції комплексної змінної |
57 |
||||
3. Якщо lim f (z) A 0, |
то існує проколений окіл U(z0) \ {z0} точ- |
||||
z z0 |
|
|
|
|
|
ки z0, такий, що f (z) 0, z U(z0) \ {z0}. |
|
||||
4. Якщо lim f (z) A, lim g(z) B, то |
|
||||
z z0 |
z z0 |
|
|
|
|
|
lim (f (z) g(z)) A B; |
|
|||
|
z z0 |
|
|
|
|
|
lim (f (z)g(z)) AB; |
|
|||
|
z z0 |
f (z) |
A,B 0. |
|
|
|
lim |
|
|||
|
|
|
|
||
|
z z0 |
g(z) |
B |
|
|
3. Неперервність функції. Функцію w f (z), задану на множи- |
|||||
ні D, називають неперервною в точці z0 D, якщо |
|||||
|
lim f (z) f (z0 ), z D. |
|
|||
|
z z0 |
|
|
|
|
Функція комплексної змінної |
|
|
|||
|
f (z) u(x, y) iv(x, y) |
|
|||
неперервна у точці z0 |
x0 iy0 тоді й лише тоді, |
коли її дійсна та уя- |
|||
вна частини — функції u(x, y) та v(x, y) неперервні в точці (x0;y0 ) за сукупністю змінних x та y.
Функцію f (z) називають неперервною на множині D, якщо вона неперервна в кожній точці множини D.
9.4. Основні елементарні функції комплексної змінної
1. Модуль комплексного числа. Модуль комплексного числа z x iy знаходять за формулою
z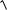
 x2 y2 .
x2 y2 .
2.Аргумент комплексного числа. Аргумент комплексного
числа z x iy визначають із співвідношень
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos |
|
|
|
|
|
|
|
, |
||
|
|
x |
2 |
y |
2 |
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
y |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
і позначають Arg z.
Значення аргументу, яке належить проміжку ( ; ] називають головним і позначають arg z. Отже,

58 |
Розділ 2. Функції комплексної змінної |
Arg z arg z 2 k, arg z ( ; ], k
3. Показникова функція. Показникову функцію ez означують для будь-якого комплексного числа z x iy співвідношенням
w ez ex iy ex (cos y i sin y).
Отже,
Re(ez ) ex cosy, Im(ez ) ex sin y; ez ex , Argez y 2 k,k .
Для x 0 дістаємо формулу Ейлера
eiy cos y i sin y.
4. Основні властивості показникової функції.
1. Для будь-яких z1 та z2 правдива теорема додавання
ez1 z2 ez1ez2 .
Нехай z1 x1 iy1,z2 x2 iy2. Тоді
ez1ez2 ex1 (cosy |
i sin y )ex2 |
(cosy |
i sin y |
2 |
) |
1 |
1 |
1 |
|
|
ex1 x2 (cos(y1 y2 ) i sin(y1 y2 ))
ex1 x2 i(y1 y2 ) e(x1 iy1 ) (x2 iy2 ) ez1 z2 .
2.Функція ez періодична з основним періодом 2 i, тобто для всіх z
ez 2 i ez .
ez 2 i eze2 i ez (cos 2 i sin 2 ) ez .
3.Функція ez неперервна на всій комплексні площині .
4.Для всіх z значення ez 0.
5.Логарифмічна функція. З рівняння
z ew
де z 0, w u iv, дістаємо
z eu, Arg z v 2 k, k u ln z , v Arg z.
Отже, обернена до функції w ez означена для будь-якого z 0 формулою
w Ln z ln |
|
z |
|
i Arg z |
|
|
|
||||
|
|
i(arg z 2 k), k . |
|||
ln |
z |
|
|||
|
|
|
|
|
|
Цю багатозначну функцію називають логарифмічною.

Лекція 9. Функції комплексної змінної |
59 |
Функцію
ln z ln z i arg z
називають головним значенням логарифму.
З формули випливає, що логарифмічна функції w Ln z має відомі властивості логарифму дійсної змінної:
Ln(z1z2 ) Ln z1 Ln z2;
Ln z1 Ln z1 Ln z2. z2
Функція w Ln z неперервна для всіх z 0.
За допомогою показникової та логарифмічної функцій комплексної змінної можна означити загальну показникову функцію
az ez Ln a,a 0.
Приклад 9.3. Записати в алгебричній формі значення:
1) e i ; 2) Ln( 1); 3) ii .
6. Степенева функція.
1. Степеневу функція цілого степеня n означують рівністю w zn n(cos n i sin n ).
Для натурального значення n дійсну та уявну частини функції w zn можна знайти за допомогою біному Ньютона.
|
|
Функція w zn |
однозначна і неперервна (крім точки |
z 0 для |
|||||||||||||||||||||
від’ємних n). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2. Степеневу функцію з показником |
1 |
, n , |
означують рів- |
||||||||||||||||||||
|
|||||||||||||||||||||||||
ністю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
n |
|
|
n |
|
|
2k |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
w z |
|
z |
|
|
|
i sin |
2k |
|
||||||||||||||
|
|
|
|
|
|
|
cos |
|
|
|
|
|
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0, n 1. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Функція w n |
|
|
n -значна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3. Загальну степеневу функцію означують рівністю |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w za |
ea Ln z . |
|
|
|
|
|
|
||||||
|
|
Функція za |
означена для всіх z 0, є багатозначною функцією. |
||||||||||||||||||||||
|
|
Приклад 9.4. |
Знайти всі значення 3 |
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
8i |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

60 |
Розділ 2. Функції комплексної змінної |
7. Тригонометричні функції. Тригонометричні функції комплексної змінної z означують рівностями:
sin z |
eiz e iz |
, |
cos z |
eiz e iz |
; |
|
2i |
2 |
|||||
|
|
|
|
|||
tg z sin z |
, |
ctg z cos z . |
|
|||
|
cos z |
|
|
sin z |
|
|
Приклад 9.4. Знайти алгебричну форму cos(i ln(5 2
 6)).
6)).
8. Властивості тригонометричних функцій. Функції sin z та cos z :
1)для дійсних z x збігаються з тригонометричними функціями sin x та cos x дійсної змінної;
2)неперервні на всій комплексній площині;
3)періодичні з періодом 2 ;
4)sin z — непарна функція, а cos z — парна;
5)зберігають відомі тригонометричні співвідношення для sin x та
cos x;
6)у комплексній площині необмежені.
lim sin z , lim cos z .
Im z Im z
Функції tgz та ctg z :
1)для дійсних z x збігаються з тригонометричними функціями tg x та ctg x дійсної змінної;
2)є періодичними з періодом ;
3)є непарними функціями;
4) означені і неперервні на всій комплексній площині, окрім
|
|
, для tgz і z k,k , для ctgz. |
|
|
|||||
z |
2 k,k |
|
|
||||||
|
9. Гіперболічні функції. Гіперболічні функції комплексної |
||||||||
змінної z означують за формулами |
|
|
|
|
|
||||
|
|
|
sh z |
ez e z |
, ch z |
ez |
e z |
, |
|
|
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
th z sh z , |
cth z ch z . |
|
|
|||
|
|
|
|
ch z |
|
|
sh z |
|
|
|
Функції sh z та ch z періодичні з періодом 2 i; |
th z та cth z періо- |
|||||||
дичні з періодом i.
10. Співвідношення між тригонометричними і гіперболіч-
ними функціями. Гіперболічні функції зв’язані із тригонометричні функціями рівностями:
