Конспект МАТАН2

де M0(x0; y0) — довільна точка неперервності функцій P та Q; C — довільна стала.

Приклад 16.1. Перевірити, що вираз du є повним диференціалом і відновити функцію u(x,y), якщо

Приклад 16.2. Перевірити, що вираз du є повним диференціалом і відновити функцію, якщо

du (2xy 3z2)dx x2dy 6xzdz.

16.3. Застосування криволінійного інтеграла 2-го роду

1. Робота векторного поля a P(x,y,z)i Q(x,y,z)j R(x,y,z)k під час переміщення вздовж кривої L від точки A до точки B.

AL(a ) Pdx Qdy Rdz.

LAB

2.Площа фігури, обмеженої замкненою кривою L.

S(D) 1 xdy ydx. 2 L

Справді, застосовуючи формулу Остроградського — Ґауса до криволінійного інтеграла маємо:

точки B(0;3).

x a cos3 t,

Приклад 16.4. Знайти площу фігури, обмеженої астроїдою

y a sin3 t.

i Ti;

n

S( ) Ti.

i 1

Площею поверхні називають

і можна вважати, що

d 1 (zx )2 (zy )2dxdy.

Якщо поверхню задано неявно рівнянням F(x,y,z) 0, то n grad F;

n grad F (Fx )2 (Fy )2 (Fz )2 ;

Отже,

d 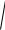(Fx )2 (Fy )2 (Fz )2 dxdy. Fz

17.4. Обчислення поверхневого інтеграла 1-го роду

Обчислення поверхневого інтеграла за поверхнею зводиться до обчислення подвійного інтеграла за областю D — проекції на одну з координатних площин.

Якщо поверхню задано рівнянням z f (x,y) і вона однозначно проекту-

ється на площину Oxy в область DOxy, то правдива формула

17.5.Застосування поверхневого інтеграла 1-го роду

1.Площа поверхні .

S( ) d .

2. Маса розподілена по поверхні з густиною (x,y,z).

m( ) (x,y,z)d .

3. Статичні моменти поверхні щодо координатних площин:

4. Координати центра мас поверхні.

Приклад 17.3. Визначити сумарний електричний заряд, розподілений на частині поверхні параболоїда 2z x2 y2, що відтинається від нього циліндром x2 y2 1, якщо густина дорівнює z.

Лекція 18. Поверхневий інтеграл 2-го роду

18.1. Орієнтація поверхні

Візьмімо на гладкій поверхні довільну точку M і виберімо в цій точці певний нормальний вектор до поверхні .

Якщо неперервно переміщувати точку M уздовж замкненого контуру, який лежить на поверхні і не перетинає її межі, то у вихідне положення точка M вернеться або з початковим, або з протилежним напрямом нормалі.

Означення 18.1. 1. Якщо на поверхні є хоча б одна точка і хоча б один контур, під час обходу якого напрям нормалі в точці зміниться на протилежний, то поверхню називають однобічною.

2. Якщо для будь-якої точки поверхні і будь-якого замкненого контуру після обходу напрям нормалі не змінюється, то поверхню називають двобічною, а сукупність усіх точок поверхні з вибраними в них напрямами нормалі нази-

вають боком такої поверхні.

Рис. 18.4. Додатний напрям обходу контуру

18.2. Потік вектора через орієнтовану поверхню

виражає наближено об’єм рідини, що протікає через всю поверхню . Отже,

18.3. Означення

Нехай в області G означено вектор-функцію

a P(x, y, z)i Q(x, y, z)j R(x, y, z)k,

де P,Q, R — неперервні в області G функції.

І нехай в області G задано кусково-гладку поверхню , орієнтовану вектором нормалі n0 n 0(M).

Розіб’ємо поверхню на ділянки i площею i і діаметром di,i 1,n.

Виберімо в кожній ділянці довільну точку Mi .

88 Розділ 2. Інтегральне числення функцій кількох змінних

(a, n)d (a, n)d (a, n)d .

3 (орієнтованість). Якщо розглянути поверхневий інтеграл за протилежним боком поверхні, то й знак інтеграла (a, n0 )d зміниться на протилежний:

(a, n0 )d (a, n0 )d .

18.5. Застосування поверхневого інтеграла 2-го роду

Потік векторного поля a Pi Qj Rk через вибраний бік поверхні .

(a ) (a,n 0)d .

Лекція 19. Скалярні і векторні характеристики векторних полів

19.1. Силові лінії векторного поля

Означення 19.1. Силовою лінією поля a називають криву, в кожній точці якої напрям дотичного вектора збігається з напрямом поля a.

також напрямлений уздовж дотичної до векторної лінії. Звідси, за означенням силової лінії, вектори

19.2. Потік векторного поля через поверхню

Нехай a Pi Qj Rk — довільне векторне поле, а — кусково-гладка поверхня.

Означення 19.2. Потоком векторного поля a через поверхню , орієнтова-

ну нормаллю n 0(M), називають поверхневий інтеграл

(a ) (a(M ), n0 )d ,

бік поверхні );

3)від зміни орієнтації поверхні знак потоку міняється на протилежний; Для замкненої поверхні :

4)якщо 0, це означає що з тіла G, яке обмежене поверхнею , виті-

кає стільки ж рідини, скільки й втікає в нього;

5)якщо 0, то рідини витікає більше, ніж втікає. Це означає, що всередині тіла G є джерело — місце де з’являється рідина;

6)якщо 0, то рідини витікає з тіла менше, ніж втікає. Це означає, що

всередині тіла G є стік — місце, це зникає рідина.