
Конспект МАТАН2
.pdf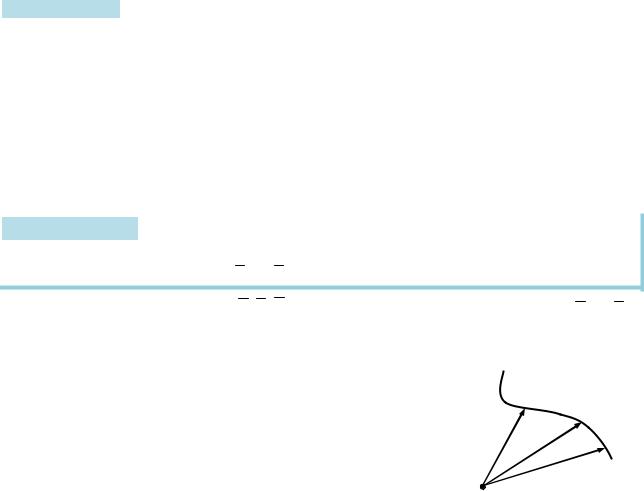
Лекція 3. Похідна за напрямом і градієнт скалярного поля |
21 |
Із встановленого геометричного змісту градієнта випливає, що градієнт не залежить від вибору системи координат, оскільки і напрям, і довжина вектора градієнта в кожній точці не залежить від вибору системи координат.
Градієнт можна розглядати для функцій будь-якої кількості змінних.
Правдиві такі правила обчислення градієнта:
1)grad(u v) grad u gradv;
2)grad(Cu) C grad u,C const;
3)grad(uv) v grad u u gradv;
4)grad u v grad u u gradv ;
vv2
5)grad f(u) fu gradu.
x2 y2
Приклад 3.2. Розподіл речовини у просторі задає функція 1 z2 . У
якому напрямі густина міняється швидше за все в точці M0( 1; 3; 2)? Визначити швидкість найбільшої зміни густини в цій точці.
3.4. Вектор-функції
У курсі вищої математики і її застосуваннях доводиться працювати не лише з числовими функціями, але й з функціями, у яких область означення D або
множина значень E складається з елементів іншої природи, приміром E 3.
Означення 3.3. Векторною функцією (вектор-функцією скалярного аргуме-
нту) називають відображення, яке кожному дійсному числу t T ставить у відповідність певний вектор r r(t).
У фіксованому базисі {i , j ,k ) задавання однієї вектор-функції r r(t) рівносильно задаванню трьох числових функцій x(t),y(t), z(t), які є її коорди-
натами: |
|
|
|
L |
|
|
|
|
|
|
||||||||||||
|
|
(t) x(t) |
i |
y(t) |
j |
z(t)k |
,t T. |
|
|
|
|
|
|
|
||||||||
r |
|
M |
|
|
|
|||||||||||||||||
Геометрично вектор-функцію зручно зображувати, |
|
|
|
|
|
|
M1 |
|||||||||||||||
будуючи множину точок простору (деяку криву) з раді- |
|
|
|
|
|
|
|
|
||||||||||||||
r (t) |
|
|
(t) |
|||||||||||||||||||
|
r |
|
|
|
||||||||||||||||||
усами-векторами |
|
|
|
1 |
|
|
M2 |
|||||||||||||||
|
|
|
|
|
|
(t),t T, |
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
r |
|
|
|
|
|
|
|
|
|
||||||||||
які виходять з фіксованої точки O. Цю множину нази- |
O |
|
|
|
|
r2(t) |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
вають годографом вектор-функції. Функція |
|
(t) задає |
|
|
|
|
|
|
||||||||||||||
r |
|
|
|
|
|
|
||||||||||||||||
параметричне зображення годографа L |
з параметром t. |
Рис. 3.6. Годограф |
|||||
вектор-функції |
|||||||
|
|
||||||
|
|
|
|
|
|
(t) |
|
|
|
r |
r |
||||
З фізичного погляду годограф вектор-функції можна розглядати як траєкторією руху матеріальної точки.

22 |
Розділ 1. Диференціальне числення функцій кількох змінних |
|
|
|
||||||||||||||||||||
|
|
Приміром, годографом функції |
|
(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ia cost jb sin t, 0 t 2 , є еліпс |
|||||||||||||||||||||
|
|
r |
||||||||||||||||||||||
|
|
|
|
a cost, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
t [0;2 ]. |
|
|
|
||||||||||||
|
із параметричними рівняннями |
b sin t, |
|
|
|
|||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.5. Границя і неперервність вектор-функції |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Означення 3.4. |
Границею вектор-функції |
|
(t) x(t) |
|
y(t) |
|
|
|
|
, коли |
|||||||||||||
|
|
i |
j |
|
z(t)k |
|||||||||||||||||||
|
r |
|||||||||||||||||||||||
|
t t0, називають сталий вектор |
|
ax |
|
ay |
|
|
|
такий, що |
|
|
|
||||||||||||
|
|
i |
j |
azk |
|
|
|
|||||||||||||||||
|
a |
|
|
|
||||||||||||||||||||
lim r (t) a
t t0
і пишуть, що lim r (t) a.
t t0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x(t) ax, |
|||
|
t t |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
, |
lim y(t) a |
||||
|
t t |
0 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
lim z(t) a |
z |
|
|
|
|
|
|
|
|
t t0 |
|
|
|
|
|
|
|
|
Властивості границь вектор-функцій можна дістати з означення і відповідних властивостей границь числових функцій.
Вектор-функцію r r (t), означену в деякому околі точки t0, називають
неперервною в точці t0, якщо
lim r (t) r (t0 ).
t t0
Вектор-функції r (t) неперервна у точці t0 тоді й лише тоді, коли коорди-
натні функції x(t),y(t), z(t) неперервні в точці t0.
3.6. Похідна вектор-функції
Нехай вектор-функція r (t) означена в деякому околі точки t0. Надамо аргумен-
ту приросту t 0 і розгляньмо приріст вектор-функції
r (t0 ) r (t0 t) r (t0 )
і відношення r (t0 ), яке є вектором, колінеарним вектору r (t0 ).
t
Означення 3.5. Похідною вектор-функції r (t) за її аргументом t в точці t0
називають вектор
|
|
|
|
|
|
|
(t0 ) |
|
lim |
|
|
(t0 |
t) |
|
(t0 ) |
. |
|
|
|
|
(t |
) lim |
r |
r |
r |
|
|||||||||
r |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
t 0 |
t |
t 0 |
t |
|
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
З того, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Лекція 4. Дотична і нормаль до кривої і поверхні |
23 |
lim
t 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
r (t |
|
t) r (t |
) |
|
||||||
0 |
|
|
||||||||
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
t |
|
|
lim |
|||
|
|
|
|
|
|
|
t 0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
x(t0 t) x(t0 ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
y(t |
|
t) y(t |
|
|
0 |
) |
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
y(t |
|
t) y(t |
|
|
0 |
) |
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
маємо, що існування |
похідної |
|
|
(t0 ) рівносильно |
|
існуванню похідних |
||||||||||||||||||||
r |
|
|||||||||||||||||||||||||
x (t0 ),y (t0 ), z (t0 ), причому правдива рівність |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r (t ) x (t )i y (t )j z (t |
|
(t |
|
||||||||||||||||||||
|
|
|
|
)k y |
|
) . |
|
|||||||||||||||||||
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приміром, знайдімо похідну вектор-функції |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
(t) |
|
|
|
|
|
|
(R,h const). |
|||||||||||||||||
|
|
iR cost jR sin t kht |
||||||||||||||||||||||||
r |
||||||||||||||||||||||||||
r (t) iR sin t jR cost kh.
Правдиві такі правила диференціювання вектор-функції:
1)(r1(t) r2(t)) r1(t) r2(t);
2)(Cr (t)) Cr (t),C const;
3)(r1(t),r2(t)) (r1(t),r2(t)) (r1(t),r2(t));
4)[r1(t),r2(t)] [r1(t),r2(t)] [r1(t),r2(t)].
Лекція 4. Дотична і нормаль до кривої і поверхні
4.1. Геометричний і механічний зміст похідної вектор-функції
Розгляньмо вектор r (t0 ) колінеарний вектору січної
t
M0M1 до кривої. Коли t 0, точка M1 прямує вздовж годографа до точки M0, і тому січна M0M1
прямує до дотичної до кривої L у точці M0, а , отже,
й вектор r (t0 ), паралельний граничному положенню
вектора січної, також буде напрямлений уздовж цієї дотичної.
M0 r (t0 )
r (t0 ) r (t0 ) L M1 O r (t0 t)
Рис. 4.1. Похідна векторфункції

24 |
Розділ 1. Диференціальне числення функцій кількох змінних |
Вектори r (t0 ) і r (t0 ) колінеарні. Якщо t 0, то ці вектори напрям-
t
лені в бік зростання t. Якщо t 0, то вектор r (t0 ) напрямлений у бік спа-
дання t, а вектор r (t0 ) знову напрямлений у бік зростання t.
t
Геометричний зміст вектора r (t0 ) полягає в тому, що він напрямлений уз-
довж дотичної до годографа функції r (t) у бік зростанням параметру t. Вектор-функція r (t) з механічного погляду задає закон руху матеріальної
точки по кривій, яка є годографом. Оскільки похідна є швидкістю змінення функції в заданій точці, то r (t0 ) є швидкістю руху матеріальної точки по цій кри-
вій, напрямленою вздовж дотичної до кривої у бік зростання t.
4.2. Дотична пряма і нормальна площина до просторової кривої
Розгляньмо гладку просторову криву L, яка прохо- |
|
|
|
|
|
|
M0 |
|
(t0 ) |
|
|||||||||||||||||||||||||||||||||
дить через точку M0(x0; y0; z0) |
і яку задано рівнянням |
|
|
|
|
|
|
r |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
x(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r r (t) |
||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t), t T. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
r r (t) y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.2. Дотична пряма |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
z(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
до кривої |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Нехай точці M0(x0; y0; z0) |
відповідає значення t0 |
параметра t. Тоді вектор |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(t |
|
) x (t |
|
) |
|
y |
(t |
|
) |
|
z |
(t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
)k |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
r |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
має напрям дотичної прямої T до кривої L у точці M0. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Запишемо канонічні рівняння дотичної до кривої L у точці M0 : |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x x0 |
|
y y0 |
|
z z0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
x (t |
0 |
) |
|
y (t |
0 |
) |
|
|
z (t |
0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Площину N, перпендикулярну до дотичної в точці дотику називають нормальною площиною до кривої в цій точці.
Нормальна площина до кривої L має рівняння
x (t0 ) x x0 y (t0 ) y y0 z (t0 ) z z0 0.
Приклад 4.1. Знайти рівняння дотичної і нормальної площини до гвинтової
лінії x a cost,y a sin t,z ht при t0 2 .

Лекція 4. Дотична і нормаль до кривої і поверхні |
25 |
4.3. Геометричний зміст градієнта
Розгляньмо поверхню , яку задає рівняння
F(x, y, z) 0.
Нехай функція F(x, y, z) диференційовна в точці M0(x0; y0; z0) , причому не всі частинні похідні в точці M0 дорівнюють нулеві.
Кажуть, що вектор n перпендикулярний до поверхні у точці M0, якщо
він перпендикулярний до будь-якої дотичної прямої, проведеної до поверхні в цій точці.
Теорема 4.1. Вектор grad u(M0 ) перпендикулярний до поверхні рівня гладкої функції u f (x,y,z) у точці M0(x0 ;y0 ;z0 ) цієї поверхні.
Розгляньмо довільну криву |
|
|
|
|
|
|
|
grad u(M0 ) |
|||||||||||||||
|
L : x x(t), y y(t), z z(t), |
|
|
|
|
u C |
|||||||||||||||||
що проходить через точку M0 |
|
поверхні рівня |
|
M0 |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
: f (x,y,z) C, |
|
|
|
|
|
|
|
L |
|
|||||||||||
де точці M0 |
відповідає значення параметра t0. |
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||
Вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.3. Геометричний зміст |
|||
|
x (t |
|
) |
|
y |
(t |
|
) |
|
z |
(t |
|
|
|
|
|
|
градієнта |
|||||
0 |
i |
0 |
j |
0 |
)k |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
напрямлений уздовж дотичної до кривої L. |
|
|
|
||||||||||||||||||||
Оскільки крива L лежить на поверхні, то координати її точок справджують |
|||||||||||||||||||||||
рівняння |
|
|
|
|
|
|
|
|
|
|
f (x(t), y(t), z(t)) C. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Диференціюючи цю рівність, маємо |
|
|
|
|
|
||||||||||||||||||
|
df (t0) |
f |
|
dx f |
|
dy) f dz |
|
0 |
(grad u(M |
0 |
), ) 0. |
||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
dt |
|
x dt |
y |
|
dt |
z dt |
|
|
|
|
||||||||||||
|
|
|
|
M |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
А це й означає ортогональність вектора grad u(M0 ) до вектора дотичної ,
і його перпендикулярність до поверхні .
4.4. Дотична площина й нормаль до поверхні
З теореми 4.1 випливає, що дотичні до всіх кривих, які проходять через точку M0 і лежать на поверхні
: F(x, y, z) 0
ортогональні до одного й того самого вектора grad F(M0 ). Тоді всі ці дотичні лежать в одній і тій
самій площині T, яку називають дотичною площиною до поверхні в точці M0.
T
M0
N
Рис. 4.4. Дотична площина і нормаль до поверхні

26 |
Розділ 1. Диференціальне числення функцій кількох змінних |
Оскільки площина T проходить через точку M0 |
перпендикулярно до вектора |
|||||||||||||||||||||||||||||||||||||||||
|
|
grad F(M |
0 |
) (F (M |
0 |
); F (M |
0 |
); F |
(M |
0 |
))T , |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
z |
|
|
|
|
|||||||||||
то її задає рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
(grad u(M0 ), MM0 ) 0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Fx (M0 )(x x0 ) Fy |
(M0 )(y y0 ) Fz |
(M0 )(z z0 ) 0. |
|
|||||||||||||||||||||||||||||||||||||||
Нормаллю до поверхні у точці M0 |
|
|
|
називають пряму N, що проходить |
||||||||||||||||||||||||||||||||||||||
через точку M0 перпендикулярно до дотичної площини T в цій точці. |
||||||||||||||||||||||||||||||||||||||||||
Оскільки нормаль проходить через точку M0 |
і її напрямним вектором є |
|||||||||||||||||||||||||||||||||||||||||
grad u(M0 ), то маємо канонічне рівняння нормалі |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x x0 |
|
|
|
y y0 |
|
|
|
|
|
|
|
z z0 |
|
. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
F (M |
0 |
) |
|
F (M |
0 |
|
|
|
|
F (M |
0 |
) |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||||
Для поверхні, заданої явно рівнянням z f (x,y) маємо: |
||||||||||||||||||||||||||||||||||||||||||
— рівняння дотичної площини |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
zx (M0 )(x x0 ) zy(M0 )(y y0 ) (z z0 ) 0; |
|
|||||||||||||||||||||||||||||||||||||||
— рівняння нормалі |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
x x0 |
|
y y0 |
|
|
z z0 |
. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
z |
(M |
0 |
) |
|
|
z (M |
0 |
) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приклад 4.2. Записати рівняння дотичної площини та нормалі до поверхні
конуса x2 y2 z2 0, M0(4; 3; 4). 16 9 8
4.5. Геометричний зміст частинних похідних
Нехай задано диференційовну функцію z f (x, y), графік якої у просторі є деякою поверхнею . Нехай M0(x0 ;y0 ) — фіксована точка з області D означення функції f , а точка N0(x0; y0; z(x0, y0)) — точка поверхні , яка відповідає точці M0.
Знаходячи частинну похідну z(M0 ) змін-
x
ну y фіксують так, що y y0.
z |
|
|
x x0 |
|
y y0 |
|
|
|
|
|
N0 |
O |
|
y |
|
|
|
|
|
M0 Ly
Lx
x
Рис. 4.5. Геометричний зміст частинних похідних

Лекція 5. Екстремуми функції двох змінних |
27 |
Геометрично, це означає, |
що через точку M0 D проводять площину |
|||||
y y0, паралельну площині Oxz, |
і розглядають функцію z f(x, y0 ) |
однієї |
||||
змінної x у точці x x0. |
|
|
|
|
|
|
Похідна цієї функції z (x |
0 |
) |
z(M0) |
дорівнює тангенсові кута |
між |
|
|
||||||
x |
|
|
x |
|
||
|
|
|
|
|
||
прямою, паралельної осі Ox, і дотичною до кривої z f (x, y0 ), що є лінією перерізу поверхні z f (x, y) із площиною y y0.
Так само частинна похідна z(M0 ) дорівнює тангенсові кута між прямою,
y
паралельної осі Oy, і дотичною до кривої z f (x0, y), що є лінією перерізу поверхні z f (x, y) із площиною x x0.
4.6. Геометричний зміст диференціала
Якщо поверхню задано в явному вигляді z f (x, y), то її можна задати неявно рівнянням f (x, y) z 0 і рівняння дотичної площини до цієї поверхні у точці M0(x0; y0; z(x0, y0 )) матиме вигляд
fx (x0, y0 )(x x0 ) fy(x0, y0 )(y y0 ) (z z0 ) 0.
Його ще можна переписати у вигляді
z fx (x0, y0 ) x fy(x0, y0 ) y df (x0, y0 ),
де x x x0, y y y0, z z z0.
Отже, диференціал функції z f (x, y) у точці (x0 ;y0 ) є приростом аплікати точки дотичної площини до поверхні z f (x, y) у точці
M0(x0 ;y0 ; z(x0, y0 )).
Лекція 5. Екстремуми функції двох змінних
5.1. Локальні екстремуми функції двох змінних
Розгляньмо функцію z f (x,y),(x;y) D. І нехай точка M0(x0 ;y0 ) D. Означення 5.1. Якщо існує окіл точки M0, який належить області D і для всіх точок M цього околу, відмінних від точки M0, виконано нерівність
f (M ) f (M0 ) (f (M ) f (M0 )),
то точку M0 називають точкою локального максимуму (мінімуму) функції f , а
число f (M0 ) — локальним максимумом (мінімумом) цієї функції.
Точки максимуму та мінімуму функції називають її точками екстремуму.

28 |
Розділ 1. Диференціальне числення функцій кількох змінних |
|
|||
|
Якщо покласти |
|
|
|
|
|
x x0 x,y y0 y, |
|
|
|
|
то повний приріст функції |
|
|
max |
|
|
|
f (x0,y0) f (x,y) f (x0,y0) |
|
z |
|
|
|
|
|
|
||
|
f (x0 x,y0 y) f (x0,y0). |
|
|
|
|
|
Якщо приріст функції зберігає знак в околі |
|
|
|
|
точки M0, то в цій точці функція має локальний |
|
O |
|
min |
|
екстремум: |
|
|
|
y |
|
|
1) максимум, якщо f (x0,y0) 0; |
x |
|
M0 |
M0 |
|
2) мінімум, якщо f (x0,y0) 0. |
Рис. 5.1. Точки локального |
|||
|
|
|
|
екстремуму |
|
5.2. Необхідна умова існування локального екстремуму
Теорема 5.1 (необхідна умова екстремуму). Якщо функція z f(x,y) має в точці M0(x0 ;y0 ) локальний екстремум, то в цій точці частинні похідні 1-го порядку за змінними x та y дорівнюють нулеві, нескінченності або не існують.
Нехай M0(x0 ;y0 ) — точка екстремуму. Тоді функція (x) f(x,y0) бу-
де функцією однієї змінної, яка має екстремум у точці x x0. Тому її похідна fx (x0,y0 ) дорівнює нулеві, нескінченності або не існує.
Так само, розглянувши функцію (y) f (x0,y), дістанемо, що fy(x0,y0 )
дорівнює нулеві, нескінченності або не існує.
Означення 5.2. Точку M0(x0;y0 ), в якій частинні похідні 1-го порядку функ-
ції f дорівнюють нулеві, називають стаціонарною точкою функції f .
У стаціонарній точці виконано також умови: dz(M0) 0, grad f (M0) 0.
Стаціонарні точки та точки, у яких частинні похідні функції дорівнюють нескінченості або не існують, називають критичними точками.
Приміром, дослідімо функцію f (x,y) 1 
 x2
x2
Функція |
f (x,y) 1 |
x2 y2 має макси- |
||||||
мум у точці (0;0), оскільки |
f (0, 0) 1, f (x,y) 1, |
|||||||
якщо x2 y2 0. |
|
|
|
|
|
|
||
Частинні похідні функції f (x,y) |
|
|
||||||
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
||
fx (x,y) |
|
x2 y2 |
|
, fy(x,y) |
x2 y2 |
|||
|
|
|
|
|
|
|||
у точці (0; 0) не існують.
y2 .
z
1
y
x
Рис. 5.2. У точці (0; 0;1) похідні не існують

Лекція 5. Екстремуми функції двох змінних
Проте не всяка критична точка є точкою екстремуму, тобто теорема встановлює лише необхідну, але не достатню умови екстремуму.
Приміром, дослідімо функцію z xy. |
z z xy |
|
Частинні похідні функції z xy дорівнюють |
|
|
нулеві в точці (0;0). Але ця функція у вказаній точці |
y |
|
екстремуму не має, тому що в досить малому околі |
O |
|
точки (0; 0) вона набуває як додатних, так і від’ємних |
x |
|
значень. Графіком функції z xy є гіперболічний |
||
|
||
параболоїд. |
Рис. 5.3. Точка O |
|
|
є сідловою точкою поверхні |
5.3. Достатні умови локального екстремуму
Нехай функція |
z f (x, y) |
двічі неперервно диференційовна в околі точки |
|||||||||||||||
M0(x0;y0 ). Якщо точка M0 |
є точкою локального екстремуму, то |
||||||||||||||||
|
f (x0,y0 ) |
0, |
f (x0,y0 ) |
0 df (M |
) |
f(M0 ) |
dx |
f (M0 ) |
dy 0. |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
y |
0 |
|
|
|
|
|
x |
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Запишімо Тейлорову формулу 1-го порядку для функції f : |
||||||||||||||||
|
|
f (M0 ) df (M0 ) |
d2f (M ) |
|
|
|
df (M0 ) 0 |
|
|
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|||||||||||||||
|
|
|
1 |
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(f (M ) x2 2f (M ) x y f |
(M ) y2 ). |
|||||||||||||
|
|
|
2 |
xx |
xy |
|
|
|
|
|
yy |
|
|
|
|
|
|
Отже, знак приросту функції f(M0 ) визначається знаком 2-го диференціала d2f .
Другий диференціал функції z f (x,y) є квадратичною формою Q(dx,dy) щодо змінних dx і dy, яку можна записати як
dx d2z (dx dy)H ,
dy
де
|
|
|
|
zxx |
zxy |
||
|
|
z |
|
H z |
— |
||
|
|
|
|
yx |
yy |
||
матриця квадратичної форми, яку називають матрицею Гессе. Визначник матриці Гессе detH називають гессіаном.
Отже d2 f (M0 ) 0 (d2f (M0 ) 0) тоді й лише тоді, коли матриця Гессе є
додатно (від’ємно) визначеною.
Згідно з критерієм Сильвестра матриця H є:
1)додатно визначеною, якщо zxx (M0 ) 0, detH(M0 ) 0;
2)від’ємно визначеною, якщо z (M ) 0, detH(M ) 0.
xx0 0

30 |
|
|
|
|
|
|
Розділ 1. Диференціальне числення функцій кількох змінних |
|
||||||||||||||||||||||||
|
|
|
0(достатні умови екстремуму функції двох змінних). |
Нехай |
||||||||||||||||||||||||||||
|
Теорема 5.2 |
|||||||||||||||||||||||||||||||
|
точка |
|
0 |
|
0 |
|
|
|
||||||||||||||||||||||||
|
|
M |
|
(x |
|
;y |
) є стаціонарною точкою функції z f (x,y), |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (M0 ) |
|
0, |
f(M0 ) |
|
0, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
і в деякому околі точки M0(x0 ;y0 ) функція f |
|
має неперервні частинні похідні |
|||||||||||||||||||||||||||||
|
до 2-го порядку включно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
A | |
2f (M |
0 |
) |
, B | |
|
2f (M |
0 |
) |
,C |
| |
|
|
|
2f (M |
0 |
) |
, |
|
||||||||
|
|
|
|
|
|
x2 |
|
|
|
x y |
|
|
|
|
|
y2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
M0 |
|
|
M0 |
|
|
|
|
|
M0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
(M0 ) detH(M0 ) |
|
A |
B |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
C |
|
M0 |
|
|
|
|
|
|||
|
Тоді: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
має екстремум, |
|
|
|
|
|||||||||
|
1) якщо (M0 ) 0, то в точці M0 |
функція f |
|
|
|
|
||||||||||||||||||||||||||
|
причому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
має мінімум; |
|
|
|
|
|
|||||||||||
|
а) якщо A 0, то функція f |
|
у точці M0 |
|
|
|
|
|
||||||||||||||||||||||||
|
б) якщо A 0, то функція f |
|
у точці M0 |
має максимум; |
|
|
|
|
||||||||||||||||||||||||
2)якщо (M0 ) 0, то в точці M0 функція f не має екстремуму;
3)якщо (M0 ) 0, то в функція f у точці M0 може мати, а може й не мати екстремуму і потребує додаткового дослідження.
Приклад 5.1. |
Дослідити на екстремум функцію z x4 |
y4. |
|
||||||||||
Знайдімо |
стаціонарні точки функції. З системи рівнянь |
|
|||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
z |
4x |
|
0, |
|
|
|
|||
|
|
|
|
x |
|
|
x 0, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4y |
0 |
|
y 0. |
|
|
|||
|
|
|
|
zy |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка M0(0; 0) — стаціонарна. |
|
|
|
|
|
|
|
||||||
A | |
z 2 |
| 0, B z |
|
| 0,C A | |
z 2 |
| 0; |
|||||||
M0 |
x |
M0 |
|
|
|
xy M0 |
0 |
M0 |
y |
M0 |
|||
|
|
|
|
|
|
(M0 ) |
0 |
0. |
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
Теорема 5.2 не дає відповідь про наявність або відсутність екстремуму. Проведімо додаткове дослідження:
f (x,y) x4 y4 f (0, 0) x 4 y4 0 M0(0; 0) min.
Приклад 5.2. Дослідити на екстремум функцію z x2 2y2 2x 4y 6.
