
- •Методичні вказівки до практичних та лабораторних
- •1. Етапи розв'язування задач моделювання
- •1.1. Моделювання
- •1.2. Постановка задачі
- •1.3. Створення математичної моделі
- •1.4. Математичне моделювання
- •1.4.1. Побудова обчислювальної моделі
- •1.4.2. Алгоритм методу
- •1.4.3. Реалізація методу обчислень
- •1.5. Контрольні запитання
- •Заняття 2. Організація обчислень
- •2.1. Джерела й види похибок
- •2.2. Запис наближених чисел. Правило округлення
- •2.3. Похибки результату при діях із наближеними числами
- •2.3.1. Похибки підсумовування
- •Розв'язування
- •2.3.2. Похибки добутку, ділення й обчислення довільної функції
- •2.4. Поширення похибок округлення при обчисленнях
- •2.5. Контрольні запитання
- •Детерміновані і стохастичні моделі.
- •Алгоритм 1
Алгоритм 1


Тестовий приклад:
M=1000; N=100; h=2.
Завдання:
Виконати алгоритм з урахуванням "вітру" (різна вірогідність кроків вправо, вліво і перевірити параболічний закон.
Модифікувати алгоритм для двомірного випадку (кроки вправо, вліво, вверх, вниз) і підрахувати середній квадрат зсуву, як x2+y2. Вивести на екран частинку.
Генератори випадкових чисел.
Звернемо увагу на 1 пункт алгоритму.
Для його реалізації необхідні випадкові числа.
Методи рішення задач, які використовують випадкові числа, називають стохастичними методами, або методами Монте-Карло. Простим генератором випадкових чисел є рулетка.
Проте через трудомісткість моделювання випадкових чисел, тільки з появою ЕОМ метод придбав широкого розповсюдження. Вважають, що він з'явився в 1949 році, а його автори - американці Дж. Нейман і С. Улам.
Наскільки хороші методи МК через їх стохастичну природу залежить від якості генератора випадкових чисел. Генератор повинен мати такі властивості:
Хороші стохастичні властивості
Ефективність
Великий період
Відтворюваність
Перший пункт - найбільш важливий. Насправді генерують не випадкові числа, а послідовність псевдовипадкових чисел. Всі генератори створюють такі послідовності за допомогою рекурентних співвідношень, використовуючи функцію залишку. Така послідовність через період повторює себе. Ефективність генератора важлива, оскільки потрібна велика кількість випадкових чисел (1010) + економія пам'яті.
Відтворюваність
потрібна для того, щоб перевірити вплив
змін в алгоритмі на результати моделювання
випадкових чисел. Прикладом алгоритму
отримання псевдовипадкових чисел може
служити запропонований Дж. Нейманом
метод середини квадратів. Чотиризначне
число зводиться в квадрат, чотири
внутрішні цифри знову в квадрат, і т.д.
Випадковими приймаються чотирьохзначні
числа
![]() .
Цей метод дає непропорційно багато
малих значень.
.
Цей метод дає непропорційно багато
малих значень.
Найбільш популярні зараз лінійні конгруентні генератори.
![]()
![]()
де
![]()
3. Випадкові блукання і розподіл вірогідності.
Ми пам'ятаємо, що мікростан системи великої кількості частинок нестійкий навіть при малих флуктуаціях. Це означає, що передбачати стан макросистеми неможливо в принципі. Мікроподії в макросистемі є істинно випадковими. Головне завдання статистичної фізики - знаходити вірогідність станів і мікроподій.
На минулому занятті ми розглянули алгоритм, що дозволяє змоделювати випадкові блукання (одновимірний випадок) ансамблю з М частинок (незалежних один від одного), і оцінити, як виконується параболічний закон дифузії (середній квадрат зсуву частинки пропорційний часу випадкових блукань). У цьому завданні ми обчислюємо середній квадрат зсуву, усереднений по ансамблю.
Сьогодні ми розглянемо подібний алгоритм, (і подібну модель), але поставимо завдання одержати на виході програми розподіл вірогідності положення частинок при випадкових одновимірних блуканнях.
Постановка завдання: нехай частинка може рухатися вправо з вірогідністю р, а вліво з вірогідністю q=1-p з однаковим кроком h. Необхідно визначити, з якою вірогідністю PN(x) через N кроків частинка знаходитиметься на відстані N від початкової точки x0=0.
Очевидно, що тут можна було б використовувати комп'ютер як генератор всіх можливих перестановок блукань. Наприклад, якщо розглянути 3 кроки випадкових блукань, то 8 можливих траєкторій виглядають таким чином:

; ; ;
; ; ;
Тобто в нас можливі два варіанти із зсувом на 3 кроки (вправо з вірогідністю р3 або вліво з вірогідністю q3) і 6 варіантів зсуву на 1 крок (3 вправо з вірогідністю p2q або три вліво з вірогідністю pq2). Тоді середній зсув:
![]()
Кількість можливих траєкторій блукань в одновимірному випадку 2N (для нашого випадку - 8), тоді для d-мірного простору підрахунок кількості блукань обмежений через громіздкість операцій.
Альтернативним варіантом може бути вибірка, статистичний характер якої дасть нам інформацію про процес в цілому. Якщо розглянути ансамбль частинок, кожна з яких незалежно від інших проходить випадковий шлях довжиної N кроків з початкової точки, то більшість частинок після однакової кількості кроків матимуть однакову координату XN. Тобто, для визначення вірогідності знаходження частинки в точці X моделюється багато її запусків (М), за якими проводиться усереднювання для визначення середнього зсуву на N кроків і визначається вірогідність появи частинки в заданій точці X як:
![]() де
m- число запусків із зсувом X.
де
m- число запусків із зсувом X.
В результаті ми одержали (графічно) розподіл вірогідності у вигляді:
PN(x)

X

Статистичний характер завдання полягає в тому, що ми розглядаємо або велику кількість випадкових блукань, або велику кількість однакових частинок, які рухаються одночасно.
Завдання:
показати, що, продовживши ці розподіли,
можна одержати другий закон Фіка (1855) -
рівняння дифузії
![]() - що говорить про те, що випадкові блукання
частинок приводять до перерозподілу
їх концентрації згідно вказаному закону.
- що говорить про те, що випадкові блукання
частинок приводять до перерозподілу
їх концентрації згідно вказаному закону.
Запишемо
алгоритм побудови графіка розподілу
вірогідності при випадкових одновимірних
блуканнях - гістограми PK(m) з шириною
стовпця
![]() .
М - число частинок, положення яких після
N кроків відповідає умові:
.
М - число частинок, положення яких після
N кроків відповідає умові:
![]()
![]()
 ;
(Nh
-
максимально можливий зсув)
;
(Nh
-
максимально можливий зсув)
Алгоритм 2

Тестовий приклад: М=1000, N=100, h=2, X=5.
Примітка 1: початок координат 320, 440, масштабний множник 2.
Координати додаткових вузлів стовпця:
(320+k2 xx 440);
(320+k2x+x 440+2pk)
Завдання: Перевірити, що одержаний розподіл - є розподілом Гауса. Використовувати метод найменших квадратів для значень ((kx)2, ln(pk)) для нульових значень масиву P, оскільки для розподілу Гауса:
![]()
![]() .
.
Щоб завершити нашу "екскурсію в область дифузії", розглянемо алгоритм моделі, яка реалізовує вакансійний механізм дифузії між атомами різного сорту методом МК.
Ми використовуватимемо модель плоских квадратних граток, кожному вузлу яких відповідає елемент масиву а. Осередки масиву (вузли) мають ознаки, по яким визначається сорт атома і вакансій (наприклад, цілі числа, які можна використовувати, як колір виведення осередків на екран). Спочатку приймемо, що права половина гратки зайнята атомами сорту А. (зелені, значення 2), ліва - атомами сорту В (блакитні - 3). Вакансію розмістимо в одному вузлі гратки, для визначеності виберемо верхній лівий кут (значення елементу масиву - 8). Нескінченність гратки nn забезпечимо граничними умовами Борна-Кармана, на кожному кроці методом МК випадково вибираємо напрям стрибка вакансії завдовжки h в одному з чотирьох можливих напрямів і міняємо місцями вакансію і вибраний атом. Задамося числом стрибків М.
Т
Поменять
местами вакансию и атом с координатами
ivnew,jvnew aiv,
jv=aivnew,
jvnew aivnew,
jvnew=8
Алгоритм 3

4. Метод молекулярної динаміки.
Основні параметри: стан і ансамблі.
У основі моделювання лежить певна модель фізичної системи, в розрахунку характеристики якої ми зацікавлені. Ці характеристики одержують як середні по простору станів системи. Позначимо стан системи як x=(x1.xn), де n- число мір свободи. Безліч станів системи складають доступний їй фазовий простір .
Систему можна описати, задаючи її мікроскопічний стан (мікростан). Такий опис дає нам найповнішу, відповідну законам механіки характеристику кожної частинки системи.
У більшому масштабі макроскопічний стан (макростан) системи можна описати за допомогою середніх концентрацій, температури, об'єму і т.д.
На відміну від непередбачуваного мікростану системи, макростан системи через деякий час перестає змінюватися. Такий стан називають рівноважним.
Якщо макростан ізольованої системи характеризується величинами N - число частинок, V - об'ємом і Е - енергією, то на мікроскопічному рівні в загальному випадку існує величезна кількість способів конфігурації, в яких може реалізуватися даний макростан (N, V, E).
Конкретний мікростан (конфігурація) є досяжним, якщо його характеристики відповідають даному макростану. У нас немає причин віддати пріоритет тому або іншому стану; і можна стверджувати, що у будь-який момент система рівномірно знаходитися в одному з своїх досяжних мікростанів (постулат рівної апріорної вірогідності).
Якщо ізольована система має досяжних рівномірних станів, то вірогідність знайти її в мікростані S складає:
PS=![]()

З погляду усереднювання за часом, фізичний сенс вірогідності PS - відрізок часу, протягом якого одна система знаходиться в мікростані S щодо всього часу спостереження.
Ансамбль, який характеризується величинами N, V, E і описується розподілом рівних апріорних імовірностей називають мікроканонічним.
У реальних (лабораторних) умовах система не замкнута, а знаходиться в тепловому контакті з навколишнім середовищем (формально - з тепловим резервуаром). Оскільки нас цікавлять рівноважні значення фізичних величин, то потрібно знати вірогідність Pl, з якою система знаходиться в стані S з енергією El. Ансамбль, який характеризується постійними величинами N, V, T і описується канонічним розподілом Гіббса:
![]()
називається канонічним.
Тут z- статистична сума.
Завдання про гармонійний осцилятор.
Метод молекулярної динаміки (МД) обчислює характеристики системи, використовуючи рівняння руху. На ПК ми чисельно вирішуємо рівняння руху, і для цього апроксимуємо їх відповідною чисельною схемою, зручною для розрахунків на ПК.
Визначення:
Метод МД розраховує у фазовому просторі траєкторії сукупності молекул, кожна з яких підкоряється класичним рівнянням руху.
Елементарний приклад - завдання про коливання тіла, рухомого під дією пружної сили - одновимірний гармонійний осцилятор.
Ми задаємо гамільтоніан, який описує рух тіла під дією пружної сили:
![]() ;
;
далі, використовуючи закони класичної механіки і розкладання в ряд Тейлора:

можна вивести рекурсивні формули для положення тіла і його імпульсу.

при цьому безперервна траєкторія руху замінюється ламаною лінією з кроком t.
Ми бачимо, що метод МД - детерміністичний: результат, одержаний на визначеному кроці визначається результатом, одержаним на попередньому кроці.
Чисельний алгоритм методу МД.
Нехай у нас є система з N частинок, і рух кожною описується диференціальними рівняннями:
![]()
Нам
потрібно згенерувати траєкторію у
фазовому просторі, тобто підрахувати
значення
![]() кожної частинки (їх сукупність дає нам
точку у фазовому просторі) у момент
часу:
кожної частинки (їх сукупність дає нам
точку у фазовому просторі) у момент
часу:
![]() .
.
Типовим методом чисельного рішення диференціальних рівнянь є їх перетворення в кінцево-різницеві.
Замінимо
похідну
![]() відношенням малого приросту функції
до приросту аргументу (переміщення x за
час t)
відношенням малого приросту функції
до приросту аргументу (переміщення x за
час t)
![]() ?.
Тобто для даної частинки в кожен момент
часу tn+1 швидкість Vn+1:
?.
Тобто для даної частинки в кожен момент
часу tn+1 швидкість Vn+1:
![]() .
.
Значить, кожне наступне положення визначається через попереднє.
![]()
застосувавши ці міркування до диференціального рівняння, одержимо формули Ейлера для знаходження швидкості і координати, як рішення диференціальних рівнянь:
![]()
Припущенням цих формул, як ми бачимо, є те, що на відрізку (t n, tn+1) швидкість зміни функції X постійна. Метод Ейлера є асиметричним - він просуває рішення на 1 крок за часом t, використовуючи при цьому інформацію про похідні тільки в початковій точці інтервалу.
Існують точніші методи:
Метод Ейлера - Камера (метод приблизно по останній точці)
![]()
Метод середньої точки - використовує для нового значення координати середню на відрізку швидкість

Метод напівкроку - використовує допущення, що швидкість на відрізку рівна значенню швидкості в середній точці відрізка

Можна порахувати:
![]()
![]() .
.
Точнішим є метод Верне.

Недолік: необхідність іншого методу для отримання перших точок фазового простору і обчислення швидкості шляхом віднімання близьких за величинами значень. При цьому втрачаються значущі цифри, і росте помилка.
Ці недоліки відсутні в швидкісній формі алгоритму Верне.

Метод Лиману і Шофілда:

Вважається кращим за алгоритм Верне, оскільки краще зберігає енергію.
Метод предіктор - коректор - використовує "передбачення" нового значення координати.
Предіктор:
![]() дозволяє обчислити прискорення,
використовуючи яке знаходимо скоректовані
значення:
дозволяє обчислити прискорення,
використовуючи яке знаходимо скоректовані
значення:
Коректор:

Скоректоване
значення
![]() використовується для обчислення
значення, що передбачаються, а значить
- нових значень, що передбачаються
використовується для обчислення
значення, що передбачаються, а значить
- нових значень, що передбачаються
![]() .
Ця процедура повторюється до тих пір,
доки значення, що передбачаються і
скоректовані, не будуть близькі.
.
Ця процедура повторюється до тих пір,
доки значення, що передбачаються і
скоректовані, не будуть близькі.
Метод Рунге- Кутта дозволяє підвищити точність методу Ейлера внаслідок екстраполяції в середній точці відрізка, а потім використовувати центральну похідну на всьому відрізку (див. курс Чисельні методи).
Для різних динамічних систем слід експериментувати з різними алгоритмами розрахунку. Однозначних переваг не має жоден метод.
5. Модель ідеального газу
На минулому занятті ми розглянули основну ідею детерміністичного методу МД, для того, щоб ми могли реалізувати на комп'ютері моделі ідеального і реального газів і досліджувати їх поведінку.
Мета дослідження моделей - перевірка основних газових законів і дослідження флуктуацій ідеального і реального газів.
Методи дослідження для моделі ідеального газу - методи МК і МД, для моделі реального газу - метод МД.
Нагадаємо, що в ідеальному газі можна нехтувати взаємодією між молекулами.
Модель ідеального газу.
У запропонованій моделі рух молекул задається у вигляді одновимірних блукань, при яких через рівні проміжки часу t (середній час між зіткненнями) швидкості змінюються випадково за допомогою генератора випадкових чисел згідно із законом:
 .
(1)
.
(1)
Тут середній квадрат випадкової функції
![]()
рівний одиниці, що забезпечує співвідношення:
![]() відоме
з молекулярно-кінетичної теорії.
відоме
з молекулярно-кінетичної теорії.
Співвідношення (1), тобто заміна максвелівського розподілу по Vx рівномірним із збереженням середнього квадрата є основним наближенням моделі.
Подальша процедура адекватна реальній ситуації. Кожне зіткнення із стінкою і переданий нею імпульс підраховується і підсумовується
![]()
а
молекули, що зіткнулися із стінкою,
рухаються по
законам пружного зіткнення. Наприклад,
якщо координата молекули
![]() виявляється
більше координати правої стінки L, то
виконується привласнення
виявляється
більше координати правої стінки L, то
виконується привласнення
![]()
Тиск
газу обчислюється за формулою
![]() .
.
Величина
P зазнає флуктуацій, але із збільшенням
часу (і числа ударів) стає асимптотою.
Фактично можна зупинитися після 6 кроків
для всіх молекул, при
![]()
Алгоритм

Закони і властивості ідеального газу.
Основним параметром є радіус молекул, які ми вважаємо твердими двомірними кулями (модель твердих сфер).
Метод розрахунку: МД тобто моменти результати зіткнень визначаються самою системою. Для цього підраховується час зіткнення всіх молекул між собою і стінками і вибирається найменше. Стінки можуть рухатися.
Алгоритм

Тестовий приклад:
T=10 K, число молекул N=20, R=1e-10м (радіус молекули), розміри посудини 1е-8м; маса - молекули кисню.
***до пункту 4.
а) i-j; i-j; Vx=Vxi-Vxj; Vy=Vyi-Vyj;
а: =Vx2+Vy2
b: =2Vx+Vy
з: =+-4R2;
d: =b2-4ac
б) якщо а=0 і b=0 або (а і d те t k:=-1;
в) якщо а=0 і b, то t k:=-cb;
г) якщо а то:
якщо d=0, то tk: =-ba
якщо d>0, то t1: =(-b+
 )а
)а
t2:
=(-b-![]() )/(2a),
)/(2a),
2.1) якщо t1t2, то tk: =t1=t2
д) знайти min час серед tk: tmol: =min(tk).
***до пункту 3
а) якщо Vxi>0, то t1: =(Lx-R-Xi)/Vxi
б) якщо Vxi<0, то t1: =(x0+R-xi)/(Vxi-Vst)
(x0 і Vst- координата і швидкість лівої стінки)
в) якщо Vyi>0, то t2: =(Ly-R-yi)/Vyi
г) якщо Vyi<0, то t2: =(R-yi)/Vyi
д) якщо t1<t2 те ti: =t1, інакше ti: =t2
е) знайти min серед ti: tst: =min(ti)
**** до пункту 6.
а) якщо dt=tst, то:
якщо rVxrdt-R, то Vnx: =-Vxr+2Vst інакше Vnx: =Vxr;
якщо r+Vxrdt+RLx, то Vnx: =-Vxr інакше Vnx: =Vxr
якщо r+Vxrdt+RLx, то Vnx: =-Vxr інакше Vnx: =Vxr
якщо r+Vyrdt-R; або r+Vyrdt+RLy, то Vny: =-Vyr, інакше Vny: =Vyr.
б) якщо dt=tmol, то
nk: =k+Vxkdt; nk: =k+Vykdt
nl: =l+Vxldt; nl: =l+Vyldt;
Sx=nl-nk; Sy: =nl-nk;
S=![]() ;
;

Завдання:
Досліджувати дію міжмолекулярних зіткнень на безповоротність.
Всі реальні процеси необоротні, що пов'язано з нестійкістю фазових траєкторій макросистем щодо малих збуджень. Якщо в якийсь момент змінити швидкості всіх молекул на протилежні, навіть мінімальне збудження не дасть їм рухатися "слід в слід" і опинитися в початковому мікростані. Якщо виконати це для попереднього алгоритму - моделі ідеального газу, то ми побачимо, що зіткнення з гладкими стінками матеріальних точок - молекул ідеального газу не вносить внесок до безповоротності процесу. Ця проблема вирішується в даному алгоритмі - моделі твердих сфер. Перевірити це практично.
Перевірити рівняння адіабати для двомірної моделі реального газу.
При включенні в модель повільного руху стінки можна досліджувати рівняння адіабати (Т(V)).
![]()
Температура розраховується через середній квадрат швидкості молекул.
![]()
Побудувати розподіл Максвела:
а) знайти середньоквадратичну швидкість
![]()
б) ввести умовну верхню межу швидкості
![]()
в)
![]() /20;
/20;
г) визначити, в який інтервал потрапляє швидкість кожної молекули і побудувати гістограму.
Це дає можливість простежити за кінетикою встановлення статистичної рівноваги. Якщо задати початкові швидкості однаковими за величиною і напрямом, у міру зіткнень гістограма з прямокутника перетвориться на розподіл Максвела.
Примітка: нагадаємо, що розподіл Максвела є окремий випадок розподілу Максвелла- Больцмана, коли нас, цікавить вірогідність швидкості або імпульсу молекул ідеального газу.

7. Перевірка закону Ома на моделі одновимірних блукань електронів в електричному полі з випадковими зіткненнями (МК - метод).
Фізична постановка завдання
Поведінка металу в електричному, тепловому або магнітному полях достатньо точно описується класичною електронною теорією Друзе-Лоренца (початок 20 століття).
Основні положення електронної теорії:
Метал складається з іонного каркаса і електронного газу: вільні електрони не пов'язані з конкретними іонами. Останні забезпечують нейтральність системи і не дають електронам розлітатися.
Рух електронів - поступальна хода вільних частинок між зіткненнями. При зіткненні електрон "забуває" передісторію.
 ;
де
T- температура в місці зіткнення.
;
де
T- температура в місці зіткнення.
Вірогідність зіткнення електрона впродовж малого часу dt пропорційна цьому часу і рівна
![]() де
де
ђ- середній час вільного пробігу (час релаксації системи), а формула (2) справедлива при dt<<ђ (для більшості металів ђ =10-14с).
Знайдемо
вірогідність того, що електрон не зазнає
зіткнень впродовж часу t. Розіб'ємо весь
часовий інтервал на відрізки
![]() .
Шукана вірогідність рівна добутку
вірогідності на кожному відрізку:
.
Шукана вірогідність рівна добутку
вірогідності на кожному відрізку:
![]()
(згідно
математичній формулі
 ).
).
Середній час до зіткнення:
 ;
де
;
де
i- вірогідність уникнути зіткнення впродовж t
ii- вірогідність зіткнення на наступному інтервалі dt.
Аналогічно:
 (звернемо увагу на множник 2)
(звернемо увагу на множник 2)
Згідно закону Ома, дія постійного електричного поля
 на метал діє постійний електричний
струм, пропорційний середній швидкості
зарядів. Тобто швидкість, а не прискорення
пропорційно силі. Цей "парадокс"
пояснюється зіткненнями електронів з
тепловими і структурними дефектами,
що необхідно враховувати в моделі через
коефіцієнт електропровідності.
на метал діє постійний електричний
струм, пропорційний середній швидкості
зарядів. Тобто швидкість, а не прискорення
пропорційно силі. Цей "парадокс"
пояснюється зіткненнями електронів з
тепловими і структурними дефектами,
що необхідно враховувати в моделі через
коефіцієнт електропровідності.
Зауваження*. Закон Ома в диференціальній формі:
Нехай на електрони газу в металі діє поле напруженості Е, тоді на кожен електрон діє зовнішня сила, тобто кожен електрон між зіткненнями повинен рухатися рівноприскорено.
Нехай t - час після останнього зіткнення;
V0- швидкість після останнього зіткнення.
Тоді:
![]() (3)
(3)
Середня
швидкість:
![]() (4) тому:
(4) тому:
![]() (5)
(5)
Щільність струму:
![]() (6)
(6)
В результаті:
![]() де
де
![]() (7)
(7)
![]() враховуючи,
що
враховуючи,
що
![]()
l - довжина провідника;
S - площа перетину.
Алгоритм

Тестовий приклад:
Е=0; Е=100 В/м; =10-14 с.
Заняття 8.
Перевірка закону Джоуля - Ленца (метод МК)
Фізична модель:
Під
час зіткнення електрони передають
гратці свою енергію, одержану за рахунок
їх прискорення зовнішнім полем. Знайдемо
енергію, яка виділяється за одиницю
часу в одиничному об'ємі. Даний об'єм
знаходиться в електричному полі з
напруженістю
![]() .
Для цього знайдемо середню зміну енергії
електрона під час зіткнення:
.
Для цього знайдемо середню зміну енергії
електрона під час зіткнення:
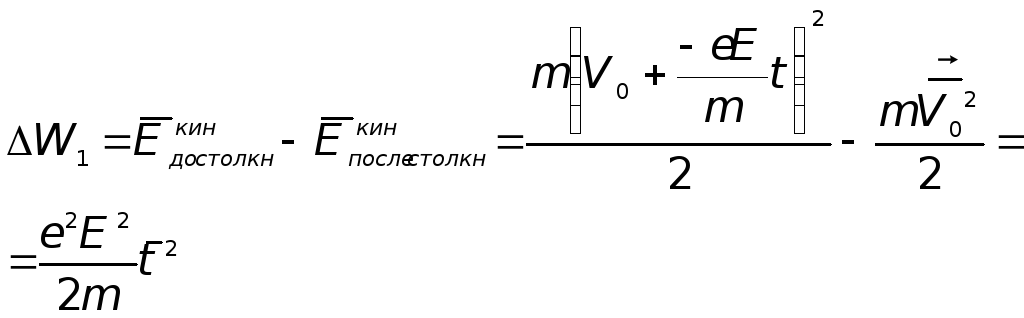
де
![]() (дивись попереднє заняття).
(дивись попереднє заняття).
Отже:
![]() ;
;
звідси:
![]() .
.
Чисельна модель.
У основу моделі покладено використання ГВЧ для часу між зіткненнями електронів з граткою.
Вважаємо, що у момент зіткнення електрон втрачає всю енергію, одержану від електричного поля.
Після усереднювання за великою кількістю зіткнень знаходимо середню енергію, яку електрон віддає кристалічній решітці за одиницю часу. Помноживши її на концентрацію електронів одержимо потужність теплових втрат за одиницю часу.
