
Лекции по ЧМ
.PDF
¨«¨ |
yi+1 , 2yi + yi,1 |
= yi00 + h2 |
|
|
|
y(IV )( +) + y(IV )( ,) |
|
||
|
h2 |
24 |
|
|
‚ १ã«ìâ ⥠¤®ª § «¨ á¯à ¢¥¤«¨¢®áâì ä®à¬ã«ë (2). •à¨ç¥¬ ãâ®ç-¨«¨ ¢¥«¨ç¨-ã |
||||
®áâ â®ç-®£® ç«¥- , ª®â®àë© ®ª § «áï à ¢-ë¬ |
|
|||
|
h2 |
|
|
|
|
24 y(IV )( +) + y(IV )( ,) |
|
||
Žç¥¢¨¤-®, çâ® íâ®â ç«¥- à ¢¥- O(h2). €- «®£¨ç-ë¬ ®¡à §®¬ ¢ë¯®«-ï¥âáï ®æ¥-ª |
||||
¯®£à¥è-®á⨠¨ ¤«ï ¤à㣨å ä®à¬ã« ç¨á«¥--®£® ¤¨ää¥à¥-æ¨à®¢ -¨ï, ¯®áâ஥--ëå - à ¢-®¬¥à-®© á¥âª¥.
12.3. —¨á«¥--®¥ ¤¨ää¥à¥-æ¨à®¢ -¨¥ á ¯®¬®éìî ᯫ ©-®¢
•à®áâë¬ á¯®á®¡®¬ ¯à¨¡«¨¦¥--®£® ¢ëç¨á«¥-¨ï ¯à®¨§¢®¤-ëå äã-ªæ¨¨ y(x) ï- ¥âáï ᯮᮡ, á®áâ®ï騩 ¢ § ¬¥-¥ ¯à®¨§¢®¤-ëå äã-ªæ¨¨ y(x) ¯à®¨§¢®¤-묨 ¨-â¥à- ¯®«ï樮--®£® ᯫ ©- , ¯®áâ஥--®£® ¯® § ¤ --ë¬ §- ç¥-¨ï¬
y(xi) = yi; i = 0; 1 : : : N:
Žâ¬¥â¨¬, çâ® ¢ ®¡é¥¬ á«ãç ¥ ¢ë¡à -- ï á¥âª -¥ ï¥âáï à ¢-®¬¥à-®©. …᫨ ¢ë- ç¨á«ïâì ¯à®¨§¢®¤-ë¥ á ¯®¬®éìî ªã¡¨ç¥áª¨å ᯫ ©-®¢, â® ¬®¦¥¬ ¢ëç¨á«¨âì ¯à®- ¨§¢®¤-ë¥ ¤® âà¥â쥣® ¯®à浪 ¢ª«îç¨â¥«ì-®. Šã¡¨ç¥áª¨© ᯫ ©- S(x) - ª ¦¤®¬ ®â१ª¥ [xi; xi+1] ¬®¦¥â ¡ëâì ¯à¥¤áâ ¢«¥- ¢ â¥à¬¨- å mi ¨ Mi:
S(x) = yi(1 , t2)(1 + 2t) + yi+1t2(3 , 2t) + mihit(1 , t)2 , mi+1hit2(1 , t)
h2
S(x) = yi(1 , t) + yi+1t , 6i t(1 , t)[(2 , t)Mi + (1 + t)Mi+1] Žâáî¤ ¢ë⥪ îâ á«¥¤ãî騥 ä®à¬ã«ë ç¨á«¥--®£® ¤¨ää¥à¥-æ¨à®¢ -¨ï:
S0(x) = 6(t2h,i |
t)(yi , yi+1) + mi(3t2 , 4t + 1) + mi+1(3t2 , 2t) |
|||||||||||
S00(x) = |
1 |
(yi+1 , yi)(6 |
, 12t) + mhi (,4 + 6t) + mhi+1 (,2 + 6t) |
|||||||||
h2 |
||||||||||||
|
|
i |
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
b |
|
|
yi+1 |
yi |
|
|
|
|
S000(x) = |
|
mi+1 + mi , 2 |
h,i |
|
|
||||
|
|
|
hi2 |
|
||||||||
|
|
|
yi+1 |
yi |
|
|
hi |
|
|
|
||
S0 |
(x) = |
|
h,i |
|
, |
6 [(2 , 6t + 3t2)Mi + (1 , 3t2)Mi+1] |
||||||
S00(x) = Mi(1 , t) + Mi+1t
S000(x) = Mi+1 , Mi
hi
‘ ¯а ªв¨з¥бª®© в®зª¨ §а¥-¨п ¡®«¥¥ ¯а¥¤¯®зв¨в¥«м-л¬¨ п¢«повбп ¯®б«¥¤-¨¥ 3 д®а- ¬г«л (§ ¯¨б --л¥ ¢ в¥а¬¨- е Mi), â.ª. ®-¨ âॡãîâ ¬¥-ì襣® ª®«¨ç¥á⢠à¨ä-
¬¥â¨ç¥áª¨å ®¯¥à 権. €«£®à¨â¬ë ¢ëç¨á«¥-¨ï ¢¥«¨ç¨- Mi ¨ mi ¯à¨¢¥¤¥-ë |
¢ëè¥. |
‘ãé¥áâ¢ãîâ ®æ¥-ª¨ â®ç-®á⨠¤«ï ä®à¬ã« ç¨á«¥--®£® ¤¨ää¥à¥-æ¨à®¢ -¨ï - |
®á-®- |
¢¥ ᯫ ©-®¢ ª ª ¢ 㧫 å á¥âª¨, â ª ¨ ¢ ¯à®¬¥¦ãâ®ç-ëå â®çª å ®â१ª [a; b]: |
|
51
13. —¨á«¥--®¥ ¨-⥣à¨à®¢ -¨¥
13.1. ‡ ¤ ç ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï
•ãáâì âॡã¥âáï - ©â¨ ®¯à¥¤¥«¥--ë© ¨-â¥£à «
b |
|
|
I = Za |
f(x) (x)dx; |
(1) |
£¤¥ äã-ªæ¨ï f(x) ¨ ¢¥á®¢ ï äã-ªæ¨ï (x) ¡®«ìè¥ -ã«ï ¨ -¥¯à¥àë¢-ë - |
®â१ª¥ |
|
[a; b]: ‚лз¨б«¨вм ¨-в¥£а « (1) в®з-® з бв® -¥ г¤ ¥вбп. •®нв®¬г ¯а¨е®¤¨вбп ¯а¨- ¡¥£ вм ª ¯а¨¡«¨¦¥--®¬г ¢лз¨б«¥-¨о ¨-в¥£а « . Ž¡лз-® дг-ªж¨о f(x) § ¬¥-пов - в ªго ¯¯а®ªб¨¬¨агойго дг-ªж¨о '(x; a) (£¤¥ a | ¢¥ªв®а ¯ а ¬¥ва ). —в®- ¡л ¨-в¥£а « ®в -¥¥ «¥£ª® ¢лз¨б«п«бп ¢ н«¥¬¥-в а-ле дг-ªж¨пе. — й¥ ¢б¥£® f(x) § ¬¥-пов -¥ª®в®ал¬ ®¡®¡й¥--л¬ ¨-в¥а¯®«пж¨®--л¬ ¬-®£®з«¥-®¬. •®бª®«мªг в - ª п ¯¯а®ªб¨¬ ж¨п «¨-¥©- ®в-®б¨в¥«м-® ¯ а ¬¥ва®¢, в® дг-ªж¨п f(x) ¬®¦¥в ¡лвм
¯à¥¤áâ ¢«¥- ¢ëà ¦¥-¨¥¬, ª®íää¨æ¨¥-â ¬¨ ª®â®à®£® á«ã¦ â §- ç¥-¨ï äã-ªæ¨¨ ¢ |
|||||
㧫 å, â.¥. |
|
n |
|
|
|
|
|
|
|
|
|
f(x) = |
|
|
f(xi)'i(x) + r(x) |
(2) |
|
|
i=0 |
|
|
|
|
|
X |
|
|
|
|
‡¤¥áì r(x) | ®áâ â®ç-ë© ç«¥- ¯¯à®ªá¨¬ 樨. •®¤áâ ¢«ïï (2) ¢ (1) ¯®«ã稬 ä®à- |
|||||
¬ã«ã ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï |
|
|
|
|
|
|
|
n |
|
|
|
I = |
X |
cif(xi) + R; |
(3) |
||
|
|
i=0 |
|
|
|
£¤¥ |
|
|
|
|
|
ci = Zab 'i(x) (x)dx |
|
||||
R = Zab r(x) (x)dx |
|
||||
‚¥«¨ç¨-ë xi - §ë¢ îâáï 㧫 ¬¨ ª¢ ¤à âãà-®© ä®à¬ã«ë, ci | ¢¥á ¬¨, R | ¯®£à¥è- |
|||||
-®áâìî ¨«¨ ®áâ â®ç-ë¬ ç«¥-®¬ ª¢ ¤à âãà-®© ä®à¬ã«ë. |
|
||||
‚¥á ci ¨ 㧫ë xi -¥ § ¢¨áïâ ®â äã-ªæ¨¨ f(x), ¯®í⮬ã ci ¬®£ãâ ¡ëâì ¢ëç¨á«¥-ë à § ¨ - ¢á¥£¤ ¤«ï ¤ --®£® ¬¥â®¤ ¨-⥣à¨à®¢ -¨ï.
‚ ¤ «ì-¥©è¥¬ ¡ã¤¥¬ ¯®« £ âì (x) 1: ‘ãé¥áâ¢ã¥â ¡®«ì讥 ç¨á«® ä®à¬ã« ç¨á«¥-- -®£® ¨-⥣à¨à®¢ -¨ï. •¥ª®â®àë¥ ¨§ -¨å à áᬮâਬ -¨¦¥.
13.2.•®áâ஥-¨¥ ä®à¬ã« ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï - ®á-®¢¥ ¨-â¥à¯®«ï樮--®£® ¬-®£®ç«¥- ‹ £à -¦
•ãáâì ¤«ï äã-ªæ¨¨ y = f(x) ¢ n + 1 â®çª å x0 : : : xn «¥¦ é¨å - ®â१ª¥ [a,b],
¨§¢¥áâ-ë ᮮ⢥âáâ¢ãî騥 §- ç¥-¨ï äã-ªæ¨¨ f(xi) = yi |
i = 0; n. ’ॡã¥âáï - ©â¨ |
¯à¨¡«¨¦¥--®¥ §- ç¥-¨¥ ¨-â¥£à « |
|
Zab f(x)dx |
(1) |
52

‡ ¬¥-¨¬ äã-ªæ¨î f(x) ¨-â¥à¯®«ï樮--ë¬ ¬-®£®ç«¥-®¬ ‹ £à -¦ .
|
n |
|
n+1(x) |
|
|
|
|
Ln(x) = |
X |
|
|
|
(2) |
||
n0 |
+1(x,i)(x |
, |
xi)yi |
||||
i=0 |
|
||||||
|
|
|
|
|
|
|
|
n+1 = (x , x0)(x , x1) : : : (x , xn)
Zb f(x)dx = Zb Ln(x)dx + R(f);
a a
£¤¥ R(f) ¯а¥¤бв ¢«п¥в б®¡®© ¯®£а¥и-®бвм, § ¢¨бпйго ®в дг-ªж¨¨ f(x). •г¤¥¬ ¨¬¥вм б«¥¤гойго ¯а¨¡«¨¦¥--го ª¢ ¤а вга-го д®а¬г«г:
b |
n |
|
|
Za |
|
|
|
X |
|
|
|
f(x)dx |
i=0 |
Aiyi |
(3); |
£¤¥
b
n+1(x)
Ai = Za n+1(xi)(x , x,i)
…б«¨ ¯а¥¤¥«л ¨-в¥£а¨а®¢ -¨п a ¨ b п¢«повбп 㧫 ¬¨ ¨-в¥а¯®«пж¨¨, в® ª¢ ¤а вга- - п д®а¬г« (3) - §л¢ ¥вбп д®а¬г«®© § ¬ª-гв®£® в¨¯ , ¢ ¯а®в¨¢-®¬ б«гз ¥, д®а- ¬г«®© ®вªалв®£® в¨¯ .
• áᬮâਬ á«ãç © à ¢-®®âáâ®ïé¨å 㧫®¢ x0 : : : xn, ª®£¤ |
x0 = a, xi = x0 + ih, |
|||||||||||||||||
xn = b, i = 0; n. ‡¤¥áì h-è £ á¥âª¨ à ¢-ë© |
b,a |
. ‚¢¥¤¥¬ ®¡®§- ç¥-¨¥ q = |
x,x0 |
. ’®£¤ |
||||||||||||||
|
h |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
||
ä®à¨¬ã«ã (2) ¬®¦-® § ¯¨á âì á«¥¤ãî騬 ®¡à § ®¬: |
|
|
|
|
||||||||||||||
Ln(x) = |
|
n |
(,1)n,i |
q(q , 1) |
, |
: : : (q , n)yi |
|
|||||||||||
|
X |
|
, |
|
i)! |
|
q |
, |
i |
|
|
|
||||||
|
i=0 i!(n |
|
|
|
|
|
|
|
|
|||||||||
’®£¤ , ¤«ï ¯à¨¡«¨¦¥--®© ª¢ ¤à âãà-®© ä®à¬ã«ë |
|
|
|
|||||||||||||||
|
|
|
xn |
|
|
|
|
n |
|
|
|
|
|
|
|
|
||
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
||||
|
|
|
Z |
f |
(x)dx i=0 Aiyi |
|
|
|
|
(4) |
||||||||
•®«ã稬 á«¥¤ãî饥 ¢ëà ¦¥-¨¥ ¤«ï ¯®áâ®ï--®£® ª®íää¨æ¨¥-â |
Ai |
|
||||||||||||||||
Ai = xn |
(,1)n,i |
q(q , 1) , |
: : : (q , n)dx: |
|
|
|
||||||||||||
Z |
|
i!(n |
, |
i)! |
|
|
(q |
, |
i) |
|
|
|
|
|||||
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
’ ª ª ª q = |
x,x0 |
, â® dx = hdq. ‚믮«-¨¬ â ª¦¥ § ¬¥-㠯।¥«®¢ ¨-⥣à¨à®¢ -¨ï. |
||||||||||||
h |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
•®«ã稬: |
|
|
|
xn q(q , 1) , |
|
|
|
|
|
|||||
|
|
Ai = (,1)n,ih |
: : : (q , n)dq: |
|
|
|||||||||
|
|
i!(n |
, |
i)! |
Z |
|
(q |
, |
i) |
|
|
|||
|
|
|
|
x0 |
|
|
|
|
|
|
||||
‡¤¥áì i ¬¥-ï¥âáï ®â 0 ¤® n. ’ ª ª ª h = |
b,a |
, â® ¬®¦¥¬ § ¯¨á âì Ai = Hi(b |
, |
a), £¤¥ |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Hi = (,1)n,ih,1 xn q , (q , 1) : : : (q , n)dq: |
|
(5) |
||||||||||
|
|
i!(n |
, |
i)! |
Z |
|
(q |
, |
i) |
|
|
|||
|
|
|
|
x0 |
|
|
|
|
|
|
||||
53

•®áâ®ï--ë¥ ª®íää¨æ¨¥-âë Hi - §ë¢ îâáï ª®íää¨æ¨¥-â ¬¨ Š®â¥á . Š¢ ¤à âãà- ï ä®à¬ã« (4) ç¥à¥§ ª®íää¨æ¨¥-âë Š®â¥á § ¯¨áë¢ ¥âáï ¢ ¢¨¤¥
b |
n |
|
|
Za |
|
|
|
X |
|
|
|
f(x)dx (b , a) |
i=0 |
Hiyi |
(6) |
”®à¬ã«ë (6) ¨ (5) - §ë¢ îâáï ä®à¬ã« ¬¨ •ìîâ®- -Š®â¥á . •¥âàã¤-® ã¡¥¤¨âìáï, çâ® ¢ë¯®«-ï¥âáï á«¥¤ãî饥 á®®â-®è¥-¨¥
n
X Hi = 1 Hi = Hn,i i=0
13.3. ”®à¬ã« âà ¯¥æ¨©
•®«®¦¨¬ ¢ ä®à¬ã«¥ (6) n=1. ’®£¤ h = b , a,
H0 = |
1 |
q(q , 1)dq = |
1 |
|
, Z |
q |
2 |
0
‘«¥¤®¢ ⥫ì-®
Zb f(x)dx
a
£¤¥ x0 = a, x1 = b.
|
1 |
q(q |
1) |
|
1 |
|
H1 = Z |
q |
,1 |
dq = |
2 |
|
0 |
|
, |
|
|
h |
(y0 + y1); |
|
|
|
(9) |
2 |
|
|
|
•â® ä®à¬ã« âà ¯¥æ¨©. ƒ¥®¬¥âà¨ç¥áª¨ ¢ ¤ --®¬ á«ãç ¥ ¬ë § ¬¥-¨¬ ªà¨¢ãî y = f(x) å®à¤®©. ˆáª®¬ë© ¨-â¥£à «, à ¢-ë© ¯«®é ¤¨ ªà¨¢®«¨-¥©-®© 䨣ãàë, § ¬¥-¨¬
-¯«®é ¤ì âà ¯¥æ¨¨.
•©¤¥¬ ¯®£à¥è-®áâì ä®à¬ã«ë âà ¯¥æ¨©.„«ï í⮣® à §«®¦¨¬ äã-ªæ¨î f(x) ¯®
ä®à¬ã«¥ ’¥©«®à , ¢ë¡¨à ï á¥à¥¤¨-ã ®â१ª [a,b] § æ¥-âà à §«®¦¥-¨ï ¨ ¯à¥¤¯®« £ ï - «¨ç¨¥ ã äã-ªæ¨¨ f(x) âॡ㥬ëå ¯® 室ã à áá㦤¥-¨ï -¥¯à¥àë¢-ëå ¯à®¨§¢®¤-ëå.
|
|
f(x) = f(x) + (x , x)f0(x) + |
1 |
|
|
|
||||||
|
|
2(x , x)0f0(x) + : : : |
(7); |
|||||||||
£¤¥ x = |
a+b |
•®£à¥è-®áâì R ä®à¬ã«ë âà ¯¥æ¨© à ¢- |
à §-®á⨠â®ç-®£® ¨ ¯à¨¡«¨- |
|||||||||
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
¦¥--®£® §- ç¥-¨© ¨-â¥£à « , â® ¥áâì |
|
|
|
|
|
|
|
|
||||
|
|
|
Za |
b |
|
|
b , a |
|
|
|
|
|
|
|
R = |
f(x)dx |
, |
(f(a) |
, |
f(b)) |
|
||||
|
|
|
|
|
2 |
|
|
|
||||
•«®ãç ¥¬, çâ® |
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
(b , a)3f00(x) |
|
(8) |
||||||
|
|
|
|
R , |
|
|
||||||
|
|
|
|
12 |
|
|||||||
—â®¡ë ¯®«ãç¨âì ä®à¬ã«ã (8), -¥®¡å®¤¨¬® ¯®¤áâ ¢¨âì ¢ëà ¦¥-¨¥ (7) ¢ ¨-â¥£à « (1), ¯à®¢¥á⨠¨-⥣à¨à®¢ -¨¥, § ⥬ ¯® ä®à¬ã«¥ (7) ¢ëç¨á«¨âì f(a) ¨ f(b) ¨ ãç¥áâì, çâ® x = a+2 b . •à¨ ¢ë¢®¤¥ (8) ®â¡à®è¥-ë ç«¥-ë, ᮤ¥à 騥 áâ à訥 ¯à¨§¢®¤-ë¥ ¡®«¥¥- ¢ë᮪¨¥ á⥯¥-¨ ¤«¨-ë ®â१ª ¨-⥣à¨à®¢ -¨ï h=b-a. ˆ§ ä®à¬ã«ë (8) ¢¨¤-®, çâ® ä®à¬ã« âà ¯¥æ¨© â®ç- ¤«ï «î¡®© «¨-¥©-®© äã-ªæ¨¨. ‚®®¡é¥ £®¢®àï ¤«¨- ®â- १ª [a,b] -¥ ¬ « , ¯®í⮬㠮áâ â®ç-ë© ç«¥- ä®à¬ã«ë R ¬®¦¥â ¡ëâì ¢¥áì¬ ¢¥«¨ª.
54
•®í⮬㠤«ï ¯®¢ëè¥-¨ï â®ç-®á⨠- ®â१ª¥ [a,b] áâநâáï ¤®áâ â®ç-® £ãáâ ï á¥â- ª a = x0 < x1 < : : : < xN = b. ˆ-â¥£à « à §¡¨¢ îâ - á㬬㠨-â¥£à «®¢ ¯® è £ ¬ á¥âª¨ ¨ ª ª ¦¤®¬ã è £ã ¯à¨¬¥-ïîâ ä®à¬ã«ã (9). •®«ãç ¥¬ ®¡®¡é¥--ãî ä®à¬ã«ã âà ¯¥æ¨©
|
|
|
|
b |
|
|
|
1 |
|
|
N |
|
|
|
|
|
|||
|
|
|
|
Za |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
(10) |
|||||
|
|
|
|
f(x)dx 2 |
|
|
|
|
(xi , xi,1)(yi,1 + yi) |
||||||||||
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
||||
•à¨ í⮬ ¯®£à¥è-®áâì ä®à¬ã«ë (10) ®¯à¥¤¥«ï¥âáï ä®à¬ã«®© |
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
N |
|
|
|
|
|
|||||
|
|
|
|
R , |
|
|
|
|
(xi , xi,1)3f00 |
(xi); |
(11), |
||||||||
|
|
12 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|||||
£¤¥ xi |
= xi,1,xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
„«ï à ¢-®¬¥à-®© á¥âª¨ ä®à¬ã«ë (10) ¨ (11) ã¯à®é îâáï. ‚¬¥áâ® (10) ¡ã¤¥¬ |
|||||||||||||||||||
¨¬¥âì |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Za |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
f(x)dx |
h(2y0 |
|
+ y1 + y2 + : : : + yN,1 + 2yN ); |
(12) |
|||||||||||||
¢¬¥áâ® (11) ¯®«ã稬 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
N |
h3f00(xi); |
|
|
|||
|
|
|
|
|
|
R , |
|
|
|
X |
|
(13) |
|||||||
|
|
|
|
|
|
12 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
£¤¥ h = xi , xi,1 = |
b,a |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
¯à ªâ¨ª¥ 㤮¡-¥¥ ¨á¯®«ì§®¢ âì ¢¬¥áâ® (13) ¬ ¦®à -â-ãî ®æ¥-ªã: |
||||||||||||||||||
|
|
|
|
|
|
|
jRj |
|
1 |
M2h3N; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
12 |
|
|
||||||||||
£¤¥ M2 = max jf00(x)j: |
b,a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
‘ ãç¥â®¬ ⮣®, çâ® h = |
n |
, ¯®á«¥¤-îî ä®à¬ã«ã ¯¥à¥¯¨è¥¬ ¢ ¢¨¤¥ |
|||||||||||||||||
|
|
|
|
|
|
jRj |
1 |
(b , a)h2M2: |
|
(14) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
12 |
|
|||||||||||
„«ï ¯à®¨§¢®«ì-®© -¥à ¢-®¬¥à-®© á¥âª¨ ®æ¥-ª |
(11) -¥ã¤®¡- |
¤«ï ¨á¯®«ì§®¢ - |
|||||||||||||||||
-¨ï. •à¨ í⮬ ¬®¦-® ¢®á¯®«ì§®¢ âìáï ä®à¬ã«®© (14), ¯®¤à §ã¬¥¢ ï ¯®¤ h max(xi , |
|
xi,1) |
i = 1; N: |
13.4. ”®à¬ã« ‘¨¬¯á®-
•®«®¦¨¬ ¢ ä®à¬ã« å •ìîâ®- -Š®â¥á |
|
|
n=2. •®«ã稬 x0 = a, x2 = b. ‘®£« á-® |
|||||||||
ä®à¬ã«¥ (5) - 室¨¬ H0 = |
1 |
,H1 = |
2 |
,H2 = |
1 |
. •à¨ í⮬ b |
, |
a = x2 |
, |
x0 = 2h. Žâáî¤ |
||
|
|
|
||||||||||
6 |
|
3 |
|
6 |
|
|
|
|||||
- 室¨¬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
h |
|
|
|
|
|
|
|
|
Za |
|
|
|
|
|
|
|
|
|
||
|
f(x)dx 3 |
(y0 + 4y1 + y2) |
|
|
|
(1) |
||||||
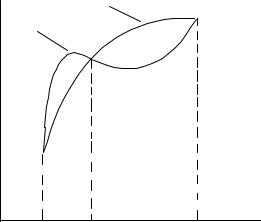
•â® ä®à¬ã« ‘¨¬¯á®- . ƒ¥®¬¥âà¨ç¥áª¨ íâ ä®à¬ã« ¯®«ãç ¥âáï ¢ १ã«ìâ ⥠§ ¬¥- -ë äã-ªæ¨¨ f(x) ¯ à ¡®«®© y = L2(x), ¯à®å®¤ï饩 ç¥à¥§ 3 â®çª¨ (x0; y0),(x1; y1),(x2; y2).
55
y |
y=L2(x) |
|
|
y=f(x) |
|
a x1 b x
—â®¡ë ®æ¥-¨âì ¯®£à¥è-®áâì ä®à¬ã«ë ‘¨¬¯á®- à áᬮâਬ à §-®áâì ¬¥¦¤ã â®ç-ë¬ ¨ ¯à¨¡«¨¦¥--ë¬ §- ç¥-¨¥¬ ¨-â¥£à « . •ã¤¥¬ ¨¬¥âì:
b |
|
h |
|
|
R = Za |
|
|
|
|
f(x)dx |
, 3 (y0 |
+ 4y1 + y2): |
|
|
• §« £ ï f(x), y0 = f(x1 ,h); |
y2 = f(x1 + h) ¢ àï¤ë ’¥©«®à ¢ ®ªà¥áâ-®á⨠â®çª¨ |
|||
x1 ¯®«гз ¥¬ б«¥¤гойго ®ж¥-ªг: |
|
|
|
|
|
h5 |
|
|
|
R , |
90f(IV )(x); |
x 2 (x0; x2) |
(2) |
|
ˆ§ ä®à¬ã«ë (2) á«¥¤ã¥â, çâ® ä®à¬ã« |
‘¨¬¯á®- (1) ï¥âáï â®ç-®©, ª®£¤ |
f(x) |
||
ï¥âáï ¬-®£®ç«¥-®¬ ¤® 3-¥© á⥯¥-¨ ¢ª«îç¨â¥«ì-®. ‘«¥¤®¢ ⥫ì-® ä®à¬ã« |
(1) |
|||
¯à¨ ®â-®á¨â¥«ì-® ¬ «®¬ ç¨á«¥ 㧫®¢ ®¡« ¤ ¥â ¯®¢ëè¥--®© â®ç-®áâìî. …᫨ ¤«¨- ®â१ª [a,b] -¥ ¬ « , â® à §®¡ê¥¬ ®â१®ª [a,b] - ç¥â-®¥ ç¨á«® ç á⥩ N=2m, ⮣¤
h = |
b,a |
. •à¨ í⮬ ¨¬¥¥¬ -¥ç¥â-®¥ ç¨á«® 㧫®¢. •à¨¬¥-¨¬ ä®à¬ã«ã (1) ª ª ¦¤®¬ã |
||||||||
|
||||||||||
|
2m |
|
|
|
|
|
|
|
|
|
㤢®¥--®¬ã ¯à®¬¥¦ãâªã [x0; x2], [x2; x4], : : : ¤«¨-ë 2h. •®«ã稬 ®¡®¡é¥--ãî ä®à¬ã«ã |
||||||||||
‘¨¬¯á®- . |
|
|
|
|
|
|
|
|
||
|
|
b |
h |
|
|
|
|
|
|
|
|
|
Za |
|
|
|
|
|
|
|
|
|
|
f(x)dx 3 (y0 + 4y1 + 2y2 |
+ 4y3 + : : : + 2yN,2 + 4yN,1 |
+ yN ) |
||||||
‘㬬¨àãï ¯®£à¥è-®áâ¨, ¯®«ãç¥--ë¥ - |
ª ¦¤®¬ 㤢®¥--®¬ ãç á⪥, - 室¨¬ |
|||||||||
|
|
|
h5 |
m |
|
|
|
|
|
|
|
|
|
R ,90 |
X |
f(IV )(xi) |
x 2 (x2i,1; x2i): |
(3) |
|||
|
|
|
|
i=1 |
|
|
|
|
|
|
ˆ§ ä®à¬ã«ë (3) ¬®¦-® ¯®«ãç¨âì ¬ ¦®à -â-ãî ®æ¥-ªã |
|
|||||||||
|
|
|
h5 |
|
|
|
M4 = maxjF (IV )(x) j |
|
||
|
|
|
jRj 90M4m; |
|
|
|||||
¨«¨ |
|
|
|
|
|
|
h4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
jRj |
|
(b , a)M4 |
(4) |
|||
|
|
|
|
180 |
||||||
Ž¡ëç-® ®¡®¡é¥-- ï ä®à¬ã« |
‘¨¬¯á®- ¤ ¥â å®à®èãî â®ç-®áâì ¯à¨ áà ¢-¨â¥«ì- |
|||||||||
-® -¥¡®«ì讬 ç¨á«¥ 㧫®¢, ¥á«¨ ⮫쪮 ¬®¤ã«ì ç¥â¢¥à⮩ ¯à®¨§¢®¤-®© f(IV )(x) -¥ ᫨誮¬ ¢¥«¨ª.
56
13.5. ”®à¬ã« •ìîâ®-
•®«®¦¨¬ ¢ ä®à¬ã« å •ìîâ®- -Š®â¥á n=3. ‚ १ã«ìâ ⥠¯®«ã稬 ª¢ ¤à âãà-ãî ä®à¬ã«ã •ìîâ®- , ª®â®àã ¥é¥ - §ë¢ îâ ä®à¬ã«®© âà¥å ¢®áì¬ëå:
|
b |
3h |
|
|
|
|
Za |
|
|
|
|
|
f(x)dx |
8 (y0 + 3y1 + 3y2 + y3); |
(5) |
||
£¤¥ x0 = a,x3 = b. Žáâ â®ç-ë© ç«¥- ä®à¬ã«ë (5) à ¢¥- |
|
||||
|
|
3h5 |
|
|
|
|
|
R 80 f(IV )(x); |
x 2 [x0; x3] |
(6) |
|
’ ª¨¬ ®¡à §®¬ ¯à¨ ®¤¨- ª®¢®¬ è £¥ h, ä®à¬ã« |
•ìîâ®- ¬¥--¥ â®ç- , 祬 ä®à¬ã« |
||||
‘¨¬¯á®- , -® íâ ä®à¬ã« |
¬®¦¥â ¡ëâì ¯à¨¬¥-¥- ¯à¨ ç¥â-®¬ ç¨á«¥ 㧫®¢. |
||||
„«ï ¯®¢ëè¥-¨ï â®ç-®á⨠¢¢®¤¨âáï ¡®«¥¥ ¬¥«ª ï á¥âª |
x0 : : : xN ¨ á®áâ ¢«ï¥âáï |
||||
®¡®¡é¥-- ï ä®à¬ã« |
•ìîâ®- . •à¨ í⮬ ç¨á«® N ¤®«¦-® ¡ëâì ªà â-® 3. |
||||
13.6. ”®à¬ã« |
á।-¨å |
|
|
|
|
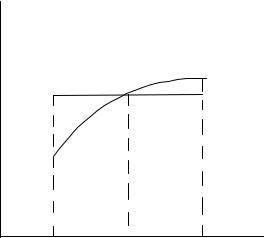
…᫨ - ®â१ª¥ [a,b] ¢§ïâì ¥¤¨-á⢥--ë© ã§¥« x0 ª¢ ¤à âãà-®© ä®à¬ã«ë, â® äã-ªæ¨ï y=f(x) ¡ã¤¥â ¯¯à®ªá¨¬¨à®¢ âìáï ¬-®£®ç«¥-®¬ -ã«¥¢®© á⥯¥-¨ (ª®-áâ -- ⮩) y0 = f(x0). •®áª®«ìªã ᨬ¬¥âà¨ï ä®à¬ã«ë ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï ¯à¨-
¢®¤¨â ª ¯®¢ëè¥-¨î ¥¥ â®ç-®áâ¨, â® ¢ë¡¥à¥¬ ¢ ª ç¥á⢥ x0 á¥à¥¤¨-ã ®â१ª |
[a,b], |
|||
x0 |
= |
a+b |
. •à¨¡«¨¦¥--® § ¬¥-ïï ¯«®é ¤ì ªà¨¢®«¨-¥©-®© âà ¯¥æ¨¨ ¯«®é ¤ìî ¯àאַ- |
|
|
||||
|
2 |
|
|
|
㣮«-¨ª , ¯®«ãç ¥¬ ä®à¬ã«ã á।-¨å (ä®à¬ã«ã ¯àאַ㣮«ì-¨ª®¢): |
|
|||
|
|
|
Zab f(x)dx (b , a)y0 |
(1) |
|
|
y |
|
|
a |
x0 |
b |
x |
|
|
|
•à¨ í⮬ ¯®£à¥è-®áâì ä®à¬ã«ë (1) ¥áâì
R |
|
(b , a)3 f00 |
(x0): |
(2) |
|
24 |
|
|
57
‘«¥¤®¢ ⥫ì-® ä®à¬ã« |
(1) â®ç- |
|
¤«ï «î¡®© «¨-¥©-®© äã-ªæ¨¨. „«ï ¯®¢ëè¥- |
|||||||||||||||||
-¨ï â®ç-®á⨠¢¢®¤¨âáï ¤®áâ â®ç-® ¬¥«ª ï á¥âª |
fx1 : : : xN g ¨ á®áâ ¢«ï¥âáï ®¡é ï |
|||||||||||||||||||
ä®à¬ã« á।-¨å: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
N |
|
|
|
|
|
|
|
xi,1+x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f(x)dx |
|
|
(xi , xi,1)3f |
) |
(3) |
|||||||||||||||
|
|
|
2 |
i |
||||||||||||||||
Za |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|||||
„«ï ®¡®¡é¥--®© ä®à¬ã«ë á।-¨å ¯®«ãç ¥¬ á«¥¤ãî騩 ®áâ â®ç-ë© ç«¥-: |
|
|||||||||||||||||||
1 |
|
N |
|
|
|
|
|
|
|
|
xi |
|
x,i |
|
1 |
|
|
|||
R |
|
|
|
(xi |
, xi,1)3f00 |
|
|
, 2 |
|
, |
|
|
(4) |
|||||||
24 |
i=1 |
|
|
|
||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• à ¢-®¬¥à-®© á¥âª¥ ä®à¬ã«ë (3) ¨ (4) ã¯à®é îâáï ¨ ¯à¨-¨¬ îâ ¢¨¤: |
|
|||||||||||||||||||
|
|
b |
|
|
|
|
|
b , a |
N |
|
|
|
|
|
h) |
|
|
|
||
|
|
f(x)dx |
|
|
f(xi |
, |
|
|
(5) |
|||||||||||
Za |
|
|
|
N |
i=1 |
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|||||
|
|
h2 |
|
|
|
|
|
M2 = max(f00(x)) |
|
|||||||||||
jRj |
24(b , a)M2 |
(6) |
||||||||||||||||||
‡ ¬¥в¨¬, зв® ®бв в®з-л© з«¥- д®а¬г«л ба¥¤-¨е ¯а¨¬¥а-® ¢¤¢®¥ ¬¥-ми¥, з¥¬ г д®а¬г«л ва ¯¥ж¨©, ¯®н⮬г, ¥б«¨ §- з¥-¨п дг-ªж¨© ®¤¨- ª®¢® «¥£ª® ¢лз¨б«повбп ¢ «о¡ле в®зª е, в® «гзи¥ ¢¥бв¨ а ббз¥в ¯® ¡®«¥¥ в®з-®© д®а¬г«¥ ба¥¤-¨е. ”®а¬г«г ва ¯¥ж¨© г¯®ва¥¡«пов ¢ в¥е б«гз пе, ª®£¤ дг-ªж¨п § ¤ - в®«мª® ¢ 㧫 е б¥вª¨,
¢ á¥à¥¤¨- å ¨-â¥à¢ «®¢ äã-ªæ¨ï -¥¨§¢¥áâ- .
13.7. —¨á«¥--®¥ ¨-⥣à¨à®¢ -¨¥ - ®á-®¢¥ ᯫ ©-®¢
Œ®¦-® ¯®áâநâì ä®à¬ã«ë ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï ¨á¯®«ì§ãï ¨-â¥à¯®«ïæ¨-
®--ë¥ á¯« ©-ë. •à¨ í⮬ äã-ªæ¨ï f(x) § ¬¥-ï¥âáï -¥ª®â®àë¬ ¨-â¥à¯®«ï樮-- |
ë¬ |
ᯫ ©-®¬ S(x) ¨ ¢ ª ç¥á⢥ ¯à¨¡«¨¦¥--®£® §- ç¥-¨ï ¨-â¥£à « |
|
Zab f(x)dx |
(1) |
¡¥à¥âáï ¢¥«¨ç¨- |
|
Zab S(x)dx: |
(2) |
•®£à¥è-®áâì ¢ëç¨á«¥-¨ï ¨-â¥£à « (1) ¬®¦¥â ¡ëâì ®æ¥-¥- á«¥¤ãî騬 ®¡à §®¬:
Zab f(x)dx , Zab S(x)dx Zab jf(x) , S(x)jdx jjf(x) , S(x)jjC (b , a) |
(3) |
‘«¥¤®¢ ⥫ì-®, ¤®áâ â®ç-® ¨¬¥âì ®æ¥-ªã ¯®£à¥è-®á⨠¯à¨¡«¨¦¥-®© äã-ªæ¨¨ f(x) ᯫ ©-®¬ S(x), ç⮡ë ᤥ« âì ®æ¥-ªã ¯®£à¥è-®á⨠ä®à¬ã«ë ç¨á«¥--®£® ¨-- ⥣à¨à®¢ -¨ï. Žâ¬¥â¨¬, çâ® ®æ¥-ªã (3) ¬®¦-® ãâ®ç-¨âì. •«®ã稬 ä®à¬ã«ã ç¨- á«¥--®£® ¨-⥣à¨à®¢ -¨ï á ¨á¯®«ì§®¢ -¨¥¬ ªã¡¨ç¥áª¨å ᯫ ©-®¢ ª« áá C2. …᫨ ¨á¯®«ì§®¢ âì ¯à¥¤áâ ¢«¥-¨¥
S(x) = fi(1 , t)2(1 + 2t) + fi+1t2(3 , 2t) + mit(1 , t)2hi , mi+1t2(1 , ,t)hi;
58

â® ¯®«ãç ¥¬
|
|
|
|
b |
|
|
|
|
N,1 , |
|
|
|
|
|
|
|
||
|
|
|
|
Z |
S(x)dx = i=0 |
Z |
xi+1S(x)dx = |
|
|
|
|
|||||||
|
|
|
|
a |
|
|
|
|
X xi |
|
|
|
|
|
|
|
|
|
|
N,1 |
|
1 |
|
|
1 |
N,1 |
|
|
|
|
1 |
|
N,,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
X |
|
|
|
|
X |
|
|
|
|
|
|
X |
|
|
|
|
|
= |
i=0 |
hi |
Z |
S(t)dt |
= |
2 |
i=0 |
hi(fi |
, |
fi+1) + |
12 |
i=0 |
(mi |
, |
mi+1)hi2 |
(4) |
||
|
|
|
|
|
|
|
|
|
|
|||||||||
• à ¢-®¬¥à-®© á¥âª¥ ¢â®à ï ä®à¬ã« |
¢ ¯à ¢®© ç á⨠ä®à¬ã«ë (4) ã¯à®é ¥âáï |
|||||||||||||||||
¨ ä®à¬ã« ¯à¨-¨¬ ¥â ¢¨¤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
b |
|
|
h |
|
|
N,1 |
|
h |
h2 |
|
|
|
|
|||
|
|
Za |
|
|
|
|
|
|
|
|
|
|||||||
|
|
S(x)dx = 2 f0 + h |
X |
fi + 2 fN + 12(m0 , mN ) |
(5) |
|||||||||||||
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
” ªâ¨ç¥áª®¥ ¯à¨¬¥-¥-¨¥ (5) -¥ âॡã¥â ¯à¥¤¢ à¨â¥«ì-®£® ¯®áâ஥-¨ï ᯫ ©- . ‚¥«¨ç¨-ë m0 ¨ mN ¬®£ãâ ¡ëâì ®¯à¥¤¥«¥-ë ®á®¡®. • ¯à¨¬¥à, ¥á«¨ S(x) 㤮¢«¥â¢®- àï¥â ªà ¥¢ë¬ ãá«®¢¨ï¬ I, â® m0 = f00, mN = fN0 . ‚ ¤à㣨å á«ãç ïå ¬®¦-® § ¬¥-¨âì m0 ¨ mN à §-®áâ-묨 ¯¯à®ªá¨¬ æ¨ï¬¨, ¯®¤®¡-묨 ⥬, ª®â®àë¥ à áᬠâਢ «¨áì ¯à¨ ¯®áâ஥-¨¨ ä®à¬ã« ç¨á«¥--®£® ¤¨ää¥à¥-æ¨à®¢ -¨ï. ‘®¢á¥¬ ¯à®áâ® ä®à¬ã«
(5) ¢ë£«ï¤¨â, ¥á«¨ f(x) ï¥âáï ¯¥à¨®¤¨ç¥áª®© äã-ªæ¨¥© á ¯¥à¨®¤®¬ b , a. ‚ í⮬ á«ãç ¥ f0 = fN ¨ m0 = mN . ‚ १ã«ìâ ⥠¯®«ã稬:
|
|
|
|
|
|
b |
|
|
N,1 |
|
|
|
|
|
|
|
|
|
|
|
|
Za |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
S(x)dx = h |
|
fi |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
•â ä®à¬ã« ᮢ¯ ¤ ¥â á ä®à¬ã«®© âà ¯¥æ¨© |
|
|
|
|
|
|
||||||||
|
|
|
Za |
b |
|
|
h |
|
|
|
|
N,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
X |
|
|
|||
|
|
|
f(x)dx |
2 (f0 + fN ) + h |
fi; |
|
|||||||||
|
|
|
|
i=1 |
|
||||||||||
â ª ª ª f0 = fN . …᫨ ¨á¯®«ì§®¢ âì ¯à¥¤áâ ¢«¥-¨¥ ᯫ ©- ¢ â¥à¬¨- å Mi |
|||||||||||||||
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
S(x) = yi(1 , t) + yi+1t , |
i |
t(1 , t)[(2 , t)Mi + (1 + t)Mi+1],; |
||||||||||||
|
6 |
||||||||||||||
â® |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Za |
|
1 |
N,1 |
|
|
|
1 |
N,1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
S(x)dx = |
2 |
X |
hi(fi |
, |
+fi+1) |
, 4 |
X |
hi3(Mi |
+ Mi+1): |
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
i=0 |
|
|
i=0 |
|
|
|
|||||
—â®¡ë ¯®«ãç¨âì ä®à¬ã«ã ¤«ï à ¢-®¬¥à-®© á¥âª¨ ¯à®é¥ ¢á¥£® ¨á¯®«ì§®¢ âì á®®â- -®è¥-¨ï
|
|
|
m0 |
= f1 , f0 |
, |
h(2M0 + M1); |
||
|
|
|
|
h |
6 |
|
|
|
|
|
|
mN = |
fN , fN,1 |
+ h |
(MN,1 + 2MN ) |
||
|
|
|
|
h |
|
6 |
|
|
¨ ¯®¤áâ ¢¨âì ¢ (5). •®«ã稬 |
|
|
|
|
|
|||
b |
5h |
|
13 |
|
|
|
N,2 |
h3 |
|
|
|
|
|
||||
S(x)dx = |
12 |
(f0 |
+ fN ) + 12h(f1 ,+fN,1) + h fi |
, 72(2M0 + M1 + MN,1 ,+2MN ) |
||||
Za |
|
|
|
|
|
|
i=2 |
|
|
|
|
|
|
|
X |
|
|
59
13.8. ”®à¬ã« ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï ƒ ãáá
‡ ¯¨è¥¬ ä®à¬ã«ã ¤«ï ç¨á«¥--®£® ¨-⥣à¨à®¢ -¨ï ¢ ®¡é¥¬ ¢¨¤¥:
b |
n |
|
|
Za |
|
|
|
X |
|
|
|
f(x) (x)dx = |
|
cif(xi) + R |
(1) |
|
i=1 |
|
|
•â ä®à¬ã« ᮤ¥à¦¨â 2n ¯ à ¬¥â஢: n 㧫®¢ xi ¨ n ¢¥á®¢ ci. ‘ва®п д®а¬г«л ва ¯¥ж¨¨, ‘¨¬¯б®- , •мов®- , ¬л § а -¥¥ § ¤ ¢ «¨ г§«л ¨ г¦¥ ¯® -¨¬ - 室¨- «¨ ¢¥б . •®н⮬㠬л -¥ ¯®«-®бвмо ¨б¯®«м§®¢ «¨ ¢®§¬®¦-®бв¨ ®¡й¥© ª¢ ¤а вга-®© д®а¬г«л (1). ’®«мª® ¢ д®а¬г«¥ ба¥¤-¨е ¬л ¯®¤®¡а «¨ ¯®«®¦¥-¨¥ 㧫 ¨§ гб«®¢¨© б¨¬¬¥ва¨¨, зв® ¯а¨¢¥«® ª бгй¥бв¢¥--®¬г г«гзи¥-¨о д®а¬г«л з¨б«¥--®£® ¨-в¥- £а¨а®¢ -¨п. ”®а¬г« (1) ᮤ¥а¦¨в 2n ¯ а ¬¥ва®¢, -® бв®«мª® ¦¥ ª®ндд¨ж¨¥-в®¢ ¨¬¥¥в ¬-®£®з«¥- бв¥¯¥-¨ 2n-1. ‡- з¨в ¯ а ¬¥вал д®а¬г«л (1) ¬®¦-® ¯®¤®¡а вм в ª, зв®¡л нв ª¢ ¤а вга- п д®а¬г« ¡л« в®з- ¤«п «о¡®£® ¬-®£®з«¥- бв¥¯¥-¨ -¥ ¢ли¥ 2n-1 ¤«п R=0. •®ª ¦¥¬ ª ª - ©в¨ - ©в¨ г§«л ¨ ¢¥б в ª®© д®а¬г«л - §л- ¢ ¥¬®© ª¢ ¤а вга-®© д®а¬г«®© ƒ гбб . •г¤¥¬ бз¨в вм, зв® ¢¥б®¢ п дг-ªж¨п (x) ¡®«ми¥ -г«п ¨ -¥¯а¥ал¢- - ¨-в¥а¢ «¥ [a,b]. Ž- ¬®¦¥в ®¡а й вммбп ¢ -г«м ¨«¨ 1 - ª®-æ å ®â१ª [a,b] â ª, ç⮡ë áãé¥á⢮¢ « ¨-â¥£à «
Zb (x)dx:
a
•à¨ ¢ë¯®«-¥-¨¨ íâ¨å ãá«®¢¨© áãé¥áâ¢ã¥â ¯®«- ï á¨á⥬ «£¥¡à ¨ç¥áª¨å ¬-®£®ç«¥- -®¢ Pn(x) ®à⮣®- «ì-ëå - ®â१ª¥ [a,b] á § ¤ --ë¬ ¢¥á®¬, â® ¥áâì
Zab Pk(x)Pn(x) (x)dx = knjjPnjj2L2 : |
(2) |
‚ᥠ-㫨 íâ¨å ¬-®£®ç«¥-®¢ Pn(x) ¤¥©á⢨⥫ì-ë ¨ à ᯮ«®¦¥-ë - |
[a,b]. |
‘®áâ ¢¨¬ ¯® 㧫 ¬ ¨-⥣à¨à®¢ -¨ï xi, ª®â®àë¥ ¯®ª - ¬ -¥¨§¢¥áâ-ë, ¬-®£®ç«¥-
n{®© á⥯¥-¨
N
n(x) = |
Y |
(x , xi): |
|
||
|
i=1 |
|
|
|
|
• áᬮâਬ äã-ªæ¨î f(x) = n(x)Pm(x) |
|
|
m (n , 1) ‚ í⮬ á«ãç ¥ f(x) | |
||
¬-®£®ç«¥- á⥯¥-¨ n+m, â® ¥áâì ¯à¨ m (n,1), f(x) ®ª § « áì ¬-®£®ç«¥-®¬ á⥯¥-¨ |
|||||
-¥ ¢ëè¥ 2n-1, -® íâ® §- ç¨â, çâ® ¤«ï â ª®© äã-ªæ¨¨ f(x), ¯® ãá«®¢¨î ¯®áâ஥-¨ï, |
|||||
ä®à¬ã« (1) ¤®«¦- ¡ëâì â®ç- , â® ¥áâì R=0. •®«ã稫¨ |
|
||||
b |
|
|
n |
|
|
Za |
|
|
|
|
|
|
|
X |
|
|
|
n(x)Pm(x) (x)dx = |
|
n(xi)Pm(xi)ci: |
(3) |
||
i=1
‡ ¬¥ç ¥¬, çâ® n(x) ¢ â®çª å xi = 0. •®«ã稬, çâ® ¯à ¢ ï ç áâì (3) ®¡à é ¥âáï ¢
0.
Zb n(x)Pm(x) (x)dx = 0: (4)
a
60
