
Лекции по ЧМ
.PDF£¤¥ M2 | - ¨¡®«ì襥 §- ç¥-¨¥ ¬®¤ã«ï ¢â®à®© ¯à®¨§¢®¤-®© - ®â१ª¥ [ ; ], m1 | - ¨¬¥-ì襥 §- ç¥-¨¥ ¬®¤ã«ï ¯¥à¢®© ¯à®¨§¢®¤-®© - ®â१ª¥ [ ; ].
M2 |
= max |
f00(x) |
; |
m1 |
= min |
f0(x) |
: |
|
[ ; ] j |
j |
|
|
[ ; ] j |
j |
|
ˆ§ á®®â-®è¥-¨ï (2) á«¥¤ã¥â, çâ® ¯®£à¥è-®áâì ®ç¥à¥¤-®£® ¯à¨¡«¨¦¥-¨ï ¯à®¯®àæ¨- ®- «ì- ª¢ ¤à âã ¯®£à¥è-®á⨠¯à¥¤ë¤ã饣® ¯à¨¡«¨¦¥-¨ï. ‡- ç¨â á室¨¬®áâì ¢ ¬¥â®¤¥ •ìîâ®- ª¢ ¤à â¨ç- ï.
‘ ¬ë© -¥¡« £®¯à¨ïâ-ë© á«ãç © ¤«ï ¬¥â®¤ •ìîâ®- , ª®£¤ f0(x) áâ -®¢¨âáï ®ç¥-ì ¬ «ë¬ ¢¡«¨§¨ ª®à-ï (£à 䨪 ¨¤¥â ¯ à ««¥«ì-® ®á¨ x).—⮡ë -¥ ¡ë«® ¯®â¥à¨
|
f(xn) |
|
|
|
§- ç é¨å æ¨äà ®â-®è¥-¨¥ |
|
á«¥¤ã¥â ¢ëç¨á«ïâì ®ç¥-ì |
ªªãà â-®. Š ®áâ «ì-ë¬ |
|
f0(xn) |
||||
¯®£à¥è-®áâï¬ à áç¥â ¬¥â®¤ •ìîâ®- å®à®è® ãá⮩稢. • |
¯à ªâ¨ª¥ ¤«ï à¥è¥-¨ï |
|||
ãà ¢-¥-¨ï f(x) = 0, ¥á«¨ f(x) ¤¨ää¥à¥-æ¨à㥬 ï äã-ªæ¨ï ¬¥â®¤ •ìîâ®- |
¯à¨¬¥-ï- |
|||
¥âáï ç é¥ ¢á¥£® ¨§-§ ¢ë᮪®© ᪮à®á⨠á室¨¬®áâ¨. Žá®¡¥--® ⮣¤ , ª®£¤ |
¨§¢¥áâ-ë |
|||
à §ã¬-ë¥ ¯à¨¡«¨¦¥-¨ï ¤«ï ª®à-¥© ¨ ª®£¤ ¯¥à¢ãî ¯ ந§¢®¤-ãî f0(x) ¢ëç¨á«¨âì |
|||||||
¤®áâ â®ç-® ¯à®áâ®. |
|
|
|
|
|
|
|
•à¨¬¥à 9. •¥è¨âì ãà ¢-¥-¨¥ f(x) = x2 , 4 = 0 |
|
|
|
||||
|
|
•¥è¥-¨¥ |
|
|
|
|
|
”®à¬ã« •ìîâ®- ¯à¨-¨¬ ¥â ¢¨¤: |
|
|
|
|
|
||
xn+1 = xn |
|
x2n , 4 = |
1 |
|
xn + |
4 |
|
, |
|
|
xn |
||||
|
2xn |
2 |
|
||||
•®¤ ¨â¥à 樨 ¯à¨¢¥¤¥¬ ¢ â ¡«¨æ¥:
n |
xn |
0 |
1 |
1 |
2.5 |
2 |
2.05 |
3 |
2.0001 |
‚¨¤¨¬, çâ® á室¨¬®áâì ®ç¥-ì ¡ëáâà ï, -¥á¬®âàï - ¯«®å®¥ - ç «ì-®¥ ¯à¨¡«¨- ¦¥-¨¥. •® ¤ ¦¥ ¯à¨ í⮬ 㦥 3-ï ¨â¥à æ¨ï ¤ ¥â â®ç-®áâì 0.005% (â®ç-ë© ª®- à¥-ì x = 2). ‡ ¬¥â¨¬, çâ® ¢¡«¨§¨ ª®à-ï ¨â¥à æ¨ï á室¨âáï á ®¤-®© áâ®à®-ë, â.¥. ¬®-®â®--®, å®âï ¯¥à¢ ï ¨â¥à æ¨ï ¤ ¥â ¯¥à¥¡à®á - ¤àã£ãî áâ®à®-ã ª®à-ï.
4.7. Œ¥â®¤ ᥪãé¨å
ˆâ¥à 樮--ë© ¯à®æ¥áá ¯® ¬¥â®¤ã •ìîâ®- |
®à£ -¨§ã¥âáï á ¯®¬®éìî ä®à¬ã«ë: |
|||
xn+1 = xn , |
f(xn) |
; |
n = 0; 1 : : : |
(1) |
f0(xn) |
||||
•à¨ í⮬ âॡã¥âáï ¢ëç¨á«¨âì ¯à®¨§¢®¤-ãî äã-ªæ¨¨ f(x), çâ® -¥ ¢á¥£¤ 㤮¡-®. Œ®¦-® § ¬¥-¨âì ¢ ä®à¬ã«¥ (1) ¯à®¨§¢®¤-ãî ª®-¥ç-®-à §-®áâ-ë¬ ®â-®è¥-¨¥¬, ¨á- ¯®«ì§ãï १ã«ìâ âë ¯®á«¥¤-¨å ¤¢ãå ¨â¥à 権:
f0(xn) f(xn) , f(xn,1): xn , xn,1
21
‚ १ã«ìâ ⥠ä®à¬ã«ã (1) ¬®¦-® § ¯¨á âì ¢ ¢¨¤¥:
xn+1 = xn |
f(xn)(xn , xn,1) |
; n = 0; 1 : : : |
(2) |
|
, f(xn) , f(xn,1) |
|
|
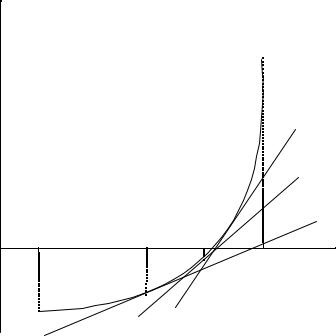
ˆâ¥à 樮--ë© ¯à®æ¥áá, ®à£ -¨§®¢ --ë© ¯® ä®à¬ã«¥ (2), - §ë¢ ¥âáï ¬¥â®¤®¬ á¥- ªãé¨å. ƒ¥®¬¥âà¨ç¥áª¨, ¢ ®â«¨ç¨¨ ®â ¬¥â®¤ •ìîâ®- , £à 䨪 äã-ªæ¨¨ y = f(x)
§ ¬¥-ï¥âáï -¥ ª á ⥫ì-®©, |
ᥪã饩. ˆ§ ä®à¬ã«ë (2) «¥£ª® ¢¨¤¥âì, çâ® ¤«ï - ç « |
¢ëç¨á«¨â¥«ì-®£® ¯à®æ¥áá |
-¥®¡å®¤¨¬® § ¤ -¨¥ x0 ¨ x1. ’ ª¨¬ ®¡à §®¬, ¯à¨ ¢ëç¨- |
б«¥-¨¨ ®з¥а¥¤-®£® ¯а¨¡«¨¦¥-¨п ¨б¯®«м§говбп ¯а¥¤л¤гй¨¥ ¤¢ , в.¥. ¬¥в®¤ б¥ªгй¨е п¢«п¥вбп ¤¢геи £®¢л¬ ¯а®ж¥бᮬ. ‚ ¨в¥а ж¨®--®¬ ¯а®ж¥бб¥ ¯® ¬¥в®¤г б¥ªгй¨е бе®- ¤¨¬®бвм ¬®¦¥в ¡лвм -¥ ¬®-®в®--®© -¥ в ®«мª® ¢¤ «¨ ®в ª®а-п, -® ¨ ¢ ¥£® ¬ «®©
®ªà¥áâ-®áâ¨. ƒ¥®¬¥âà¨ç¥áª¨ ¨â¥à 樮--ë© ¯à®æ¥áá ¢ë£«ï¤¨â á«¥¤ãî騬 ®¡à §®¬:
6y
-
x
Œ®¦-® ¯®ª § âì, çâ® á室¨¬®áâì ¨â¥à 権 ¢ ¬¥â®¤¥ ᥪãé¨å ¡®«¥¥ ¬¥¤«¥-- ï,
祬 ¢ ¬¥â®¤¥ •ìîâ®- . Ž¤- ª®, ¢ ¬¥â®¤¥ •ìîâ®- - |
ª ¦¤®© ¨â¥à 樨 á«¥¤ã¥â |
¢ëç¨á«ïâì ¨ §- ç¥-¨¥ äã-ªæ¨¨, ¨ §- ç¥-¨¥ ¯à®¨§¢®¤-®©, |
¢ ¬¥â®¤¥ ᥪãé¨å ⮫ì- |
ª® §- ç¥-¨¥ äã-ªæ¨¨. ‘«¥¤®¢ ⥫ì-®, ¯à¨ ®¤¨- ª®¢®¬ ®¡ê¥¬¥ ¢ëç¨á«¥-¨©, ¢ ¬¥â®¤¥ ᥪãé¨å ¬®¦-® ᤥ« âì ¢¤¢®¥ ¡®«ìè¥ ¢ëç¨á«¥-¨© ¨ ¯®«ãç¨âì ¢ १ã«ìâ ⥠¡®«¥¥ ¢ë- ᮪ãî â®ç-®áâì. ‡ ¬¥â¨¬, çâ® ¢ §- ¬¥- ⥫¥ ä®à¬ã«ë (2) á⮨â à §-®áâì äã-ªæ¨©, ¯à¨ç¥¬ ¢¡«¨§¨ ª®à-ï §- ç¥-¨ï äã-ªæ¨© f(xn) ¨ f(xn,1) ¬ «ë ¨ ¡«¨§ª¨ ¬¥¦¤ã ᮡ®©. ‘«¥¤®¢ ⥫ì-®, ¢®§¬®¦- ¯®â¥àï §- ç é¨å æ¨äà , ¯à¨¢®¤ïé ï ª à §¡®«âª¥ áç¥â . •â®â ä ªâ ®£à -¨ç¨¢ ¥â â®ç-®áâì. Žâ¬¥â¨¬ â ª¦¥, çâ® ¯à¨¢®¤¨âì ä®à¬ã«ã (2) ª ®¡é¥¬ã §- ¬¥- ⥫î -¥ á«¥¤ã¥â. •â® ¯à¨¢¥¤¥â ª ¯®â¥à¥ â®ç-®á⨠à áç¥â .
•à¨¬¥à 10. Œ¥â®¤®¬ ᥪãé¨å à¥è¨âì ãà ¢-¥-¨¥ f(x) x2 ,4 = 0:x0 = 1; x1 = 2:5 (ª ª ¨ ¢ ¯à¨¬¥à¥ á ¬¥â®¤®¬ •ìîâ®- ).
•¥è¥-¨¥
22
•¥§ã«ìâ âë ¢ â ¡«¨æ¥:
n |
0 |
1 |
2 |
3 |
|
|
|
|
|
xn |
1 |
2.5 |
1.8571 |
1.9836 |
…᫨ १ã«ìâ âë ¯à¨¡«¨¦¥-¨ï áà ¢-¨âì á १ã«ìâ â ¬¨, ¯®«ãç¥--묨 á ¯®¬®- éìî ¬¥â®¤ •ìîâ®- , â® ¬®¦-® ᤥ« âì ¢ë¢®¤, çâ® á室¨¬®áâì ¬¥â®¤ ᥪãé¨å ¡®«¥¥ ¬¥¤«¥-- ï.
5. •¥è¥-¨¥ á¨á⥬ -¥«¨-¥©-ëå ãà ¢-¥-¨©.
5.1. ‘¨á⥬ë -¥«¨-¥©-ëå ãà ¢-¥-¨©.
‘¨á⥬ã -¥«¨-¥©-ëå ãà ¢-¥-¨© ¬®¦-® ªà ⪮ § ¯¨á âì ¢ ¢¥ªâ®à-®¬ ¢¨¤¥
f(x) = 0
£¤¥
x = (x1 ; : : : ; xn) |
|
f = (f1; : : : ; fn)T |
|
¨«¨ ¢ ª®®à¤¨- â-®© ä®à¬¥ |
|
fk(x1; : : : ; xn) = 0; |
k = 1; 2; : : : ; n: |
•à¨ à¥è¥-¨¨ á¨á⥬ -¥«¨-¥©-ëå ãà ¢-¥-¨© ¢ ¦-® § ¤ âì å®à®è¥¥ - ç «ì-®¥ ¯à¨¡«¨¦¥-¨¥, ¢ á«ãç ¥ 2{å ¯¥à¥¬¥--ëå - ç «ì-®¥ ¯à¨¡«¨¦¥-¨¥ ¬®¦-® - ©â¨ £à ä¨- ç¥áª¨, ¤«ï í⮣® - ¯«®áª®á⨠x1x2 á«¥¤ã¥â ¯®áâநâì £à 䨪 ªà¨¢ëå f1(x1 x2) = 0
¨f2(x1 x2) ¨ - ©â¨ ¨å â®çª¨ ¯¥à¥á¥ç¥-¨ï.
‚á«ãç ¥ 3{å ¨ ¡®«¥¥ ¯¥à¥¬¥--ëå 㤮¢«¥â¢®à¨â¥«ì-ëå ᯮᮡ®¢ ¯®¤¡®à - ç «ì-
-ëå ¯à¨¡«¨¦¥-¨© -¥â.
5.2.Œ¥â®¤ ¨â¥à 権 (¬¥â®¤ ¯®á«¥¤®¢ ⥫ì-ëå ¯à¨¡«¨¦¥- -¨©).
•ãáâì âॡã¥âáï - ©â¨ à¥è¥-¨¥ á¨á⥬ë -¥«¨-¥©-ëå ãà ¢-¥-¨© |
|
f(x) = 0 |
(1) |
‡ ¬¥-¨¬ (1) íª¢¨¢ «¥-â-®© á¨á⥬®©: |
|
x = '(x) |
(2) |
£¤¥ ' = ('1; : : : ; 'n)T .
‚롥६ -¥ª®â®à®¥ - ç «ì-®¥ ¯à¨¡«¨¦¥-¨¥ x(0). ‚ëç¨á«¥-¨¥ ¤ «ì-¥©è¨å ¯à¨- ¡«¨¦¥-¨© ®áãé¥á⢫ï¥âáï ¯® ä®à¬ã« ¬
x(s+1) = '(x(s)); |
s = 0; 1; : : : |
(3) |
|
¨«¨ ¢ ª®®à¤¨- â-®¬ ¢¨¤¥ |
|
|
|
x(s+1) |
= 'k(x(s)); |
k = 1; : : : ; n |
(30) |
k |
|
|
|
23

…᫨ ¨â¥à 樮--ë© ¯à®æ¥áá á室¨âáï, â® ®-¨ á室ïâáï ª à¥è¥-¨î á¨á⥬ë (1), ¯à¨ í⮬ ¯à¥¤¯®« £ ¥âáï, çâ® à¥è¥-¨¥ á¨á⥬ë áãé¥áâ¢ã¥â.
ˆáá«¥¤ã¥¬ á室¨¬®áâì ¨â¥à 権. Ž¡®§- 稬 à¥è¥-¨¥ á¨á⥬ë ç¥à¥§( 1; : : : ; n) ¨ ¯à¥®¡à §ã¥¬ ¯®£à¥è-®áâì ®ç¥à¥¤-®© ¨â¥à 樨:
(s+1) |
|
n |
(s) |
|
@'k( k) |
, k = 'k(x(s)) , 'k( ) = |
X |
|
|||
xk |
(xi |
, i) |
@xi |
||
|
|
i=1 |
|
|
|
£¤¥ k{-¥ª®â®àë© ¯à®¬¥¦ãâ®ç-ë© ®¤-®¬¥à-ë© ¬ áᨢ.
•®á«¥¤-¥¥ à ¢¥-á⢮ ®§- ç ¥â, çâ® ¢¥ªâ®à-ë¥ ¯®£à¥è-®á⨠-®¢®£® s + 1 ¯à¨¡«¨- ¦¥-¨ï à ¢-ë ¬ âà¨æ¥ ¯à®¨§¢®¤-ëå, ã¬-®¦¥--®© - ¢¥ªâ®à-ë¥ ¯®£à¥è-®á⨠¯à¥¤ë-
¤ã饣® s{£® ¯à¨¡«¨¦¥-¨ï. Œ âà¨æ ¯à®¨§¢®¤-ëå ¨¬¥¥â í«¥¬¥-âë |
@'k( k) |
|
ɇǬ |
|
@xi |
n n |
|
ª ª ï--¨¡ã¤ì -®à¬ ¬ âà¨æë ¯à®¨§¢®¤-ëå ¬¥-ìè¥ 1, â® -®à¬ ¯®£à¥è-®á⨠|
ã¡ë- |
||
¢ ¥â ®â ¨â¥à 樨 ª ¨â¥à 樨 ¯® £¥®¬¥âà¨ç¥áª®© ¯à®£à¥áᨨ, çâ® ®§- ç ¥â «¨-¥©-
-ãî á室¨¬®áâì ¬¥â®¤ . • |
¯à ªâ¨ª¥ 㤮¡-¥¥ à áᬠâਢ âì ¬ âà¨æã á í«¥¬¥-â ¬¨ |
||||||||||||
Mki |
= max |
|
@'k |
•®à¬ë í⮩ ¬ âà¨æë ¬ ¦®à¨àãîâ ᮮ⢥âáâ¢ãî騥 -®à¬ë ¬ âà¨- |
|||||||||
|
@xi |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æë ¯à®¨§¢¥¤¥-¨©, ¯®í⮬㠤®áâ â®ç-ë¬ ãá«®¢¨¥¬ á室¨¬®á⨠¨â¥à 樮--®£® ¯à®- |
|||||||||||||
æ¥áá |
ï¥âáï ãá«®¢¨¥: |
k |
Mki |
k |
< 1. •à¨ ¨á¯®«ì§®¢ -¨¨ à §«¨ç-ëå -®à¬ íâ® ãá«®¢¨¥ |
||||||||
|
|
|
|
|
|
|
|
|
|
n |
n |
||
¬®¦¥â ¡ëâì § ¯¨á -®, - ¯à¨¬¥à, á«¥¤ãî騬 ®¡à §®¬: |
|
i=1 Mki < 1 ¨«¨ |
k=1 Mki < 1 |
||||||||||
¨«¨ |
n |
|
n |
2 |
|
|
|
|
|
P |
|
P |
|
i=1 |
P |
k=1 |
Mki < 1 ¨ ¤à. |
|
|
|
|
||||||
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
‚ᥠ-®à¬ë ¬ âà¨æë íª¢¨¢ «¥-â-ë, â.¥. ¥á«¨ ¨â¥à 樨 á室ïâáï ¢ ®¤-®© -®à¬¥, |
|||||||||||||
â® ®-¨ á室ïâáï ¨ ¢ ¤à. -®à¬ å. ’.ª. á室¨¬®áâì «¨-¥©- , â® ®ª -稢 âì ¨â¥à 樨 ¬®¦-® ¯® ªà¨â¥à¨î á室¨¬®áâ¨, ª®â®àë© ¯à¨¢¥¤¥â ¯à¨ à áᬮâà¥--®¬ ¬¥â®¤¥ ¨â¥- à 権 ª à¥è¥-¨î ®¤-®£® -¥«¨-¥©-®£® ãà ¢-¥-¨ï. •à¨ í⮬ ¢ë¯®«-塞®áâì ªà¨â¥à¨ï á«¥¤ã¥â âॡ®¢ âì ¤«ï ª ¦¤®© ª®¬¯®-¥-âë. Šà¨â¥à¨© á室¨¬®á⨠¨¬¥¥â ¢¨¤:
(xi(s+1) |
, xi(s))2 |
< " |
( ) |
||
(s) |
|
||||
(s+1) |
(s,1) |
|
|
||
j2xi |
, xi |
|
, xi |
j |
|
|
|
||||
‘ ¬¨ ¢ëç¨á«¥-¨ï ¢ ¬¥â®¤¥ ¨â¥à 権 ¯à®áâë, -® á«®¦-® ¯®¤®¡à âì â ªãî á¨á⥬ã, x = '(x) ª®â®à ï ¡ë« ¡ë íª¢¨¢ «¥-â- á¨á⥬¥ (1) ¨ ®¤-®¢à¥¬¥--® ®¡¥á¯¥ç¨¢ «® á室¨¬®áâì ¨â¥à 権. ‘室¨¬®áâì ¬¥â®¤ ¬®¦-® ã«ãçè¨âì, ¥á«¨ - ¤ --®© s + 1 ¨â¥à 樨 ¨á¯®«ì§®¢ âì 㦥 - ©¤¥--ë¥ "ᢥ¦¨¥" s + 1 ¯à¨¡«¨¦¥-¨ï ¤«ï ®â¤¥«ì-ëå ª®¬¯®-¥-â, â.¥. ¢ëç¨á«¥-¨ï ¯à®¢®¤¨âì ¯® ä®à¬ã«¥:
x(s+1) |
= 'k(x(s+1) |
; x(s+1) |
; : : : ; x(s+1) |
; x(s); x(s) |
|
; : : : ; x(s)); |
k |
1 |
2 |
k,1 |
k k+1 |
n |
|
|
|
|
k = 1; : : : ; n; |
s = 0; 1; : : : |
||
•à¨¬¥à 11. Œ¥â®¤®¬ ¨â¥à 権 - ©â¨ ¯®«®¦¨â¥«ì-ë¥ ª®à-¨ á¨á⥬ë:
f1(x1x2) |
= |
2x2 |
, |
x1x2 |
, |
5x1 + 1 = 0 |
|
|
|
1 |
|
2 |
|
||
f2(x1x2) |
= |
x1 + 3 lg x1 |
, x2 |
= 0 |
|||
•¥è¥-¨¥.
‘âந¬ - ¯«®áª®á⨠x1x2 £à 䨪¨ äã-ªæ¨© f1(x1x2) ¨ f2(x1x2)
24

x2 |
|
6 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2.2 |
|
|
|
f2(x1; x2) = 0 |
|
2 |
|
|
|
|
|
1 |
|
|
|
f1(x1; x2) = 0 |
|
|
|
|
|
||
|
|
|
- |
|
|
|
1 |
|
2 3 3.5 4 x1 |
||
|
|
|
|
|
|
•à¨¡«¨¦¥--ë¥ §- ç¥-¨ï ª®à-¥© ¥áâì x0 |
= 3:5; x0 = 2:2. ˆá室-ãî á¨á⥬㠧 ¬¥-¨¬ |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
íª¢¨¢ «¥-â-®©. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 = s |
x1(x2 +2 5) , 1 |
'1(x1x2) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 = |
x1 + 3 lg x1 '2(x1x2) |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
@'1q |
|
|
|
|
|
|
x2 + 5 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
@x1 |
|
|
x1(x2 +2 5) , 1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 + |
|
3M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
@'1 |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= p |
|
|
|
|
|
|
|
|
£¤¥ |
|
|
|
M = 0; 43429 |
||||||||||||||||||||
@x1 |
x1 + 3 lg x1 |
|
||||||||||||||||||||||||||||||||
|
@'1 = |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
@'2 = 0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
@x2 |
|
|
4s |
x1 |
(x2 +2 5) , 1 |
|
|
|
|
@x2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ž£à -¨ç¨¢ ïáì ®ªà¥áâ-®áâìî R = fjx1 , 3; 5j 0; 1; jx2 , 2; 2j 0; 1g |
||||||||||||||||||||||||||||||||||
|
|
|
@'1 |
|
|
|
|
|
|
|
2; 3 + 5 |
|
|
|
|
|
|
< 0; 54 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
@x1 |
|
4s |
3; 4(2; 1 + 5) |
, |
1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
@'1 |
|
|
|
|
|
|
|
|
|
|
|
|
3; 6 |
|
|
|
|
|
|
|
< 0; 27 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
@x2 |
|
4s |
3; 4(2; 1 + 5) |
, |
1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
@'2 |
|
|
|
|
|
|
1 + 3 0:43 |
|
|
|
@'1 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3:4 |
|
|
|
|
< 0:42 |
|
|
|
= 0 |
|||||||||||
|
|
|
2p |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
@x1 |
|
3:4 + 3 lg 3:4 |
|
|
|
@x2 |
|
||||||||||||||||||||||||||
‘«¥¤®¢ ⥫ì-®, ¥á«¨ ¯®á«¥¤ãî騥 ¯à¨¡«¨¦¥-¨ï xs |
¨ xs -¥ ¯®ª¨-ãâ ®¡« áâì R, çâ® |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
«¥£ª® ¯à®¢¥à¨âì ¢ ¯à®æ¥áᥠ¢ëç¨á«¥-¨ï, â® ¨â¥à 樮--ë© ¯à®æ¥áá ¡ëáâà® á室¨âáï.
25
…᫨ -¥ ®£à -¨ç¨¢ âì ®¡« áâì R, â® á«¥¤ã¥â ¢ëïá-¨âì ãá«®¢¨ï á室¨¬®á⨠¤«ï ¢á¥å §- ç¥-¨© x1; x2, â.¥. ®âë᪠âì ¬ ªá¨¬ã¬ ¬®¤ã«¥© ¢á¥å ¯à®¨§¢®¤-ëå - ¢á¥© ¯«®áª®á⨠x1; x2. …᫨ ãá«®¢¨ï á室¨¬®á⨠¯à¨ í⮬ ¢ë¯®«-¥-ë, â® ª®-âà®«ì § ¯à¨¡«¨¦¥-¨ï¬¨ xs1; xs2 ®áãé¥á⢫ïâì -¥â - ¤®¡-®áâ¨.
‚ëç¨á«¥-¨ï ¯à®¢®¤¨¬ ¯® ä®à¬ã« ¬:
|
|
s |
x1s(x2s |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 5) 1 |
|
|
|
|
|
|
|
|
|
|
||||
xs+1 |
= |
|
|
|
, |
|
|
|
xs+1 |
= |
q |
xs |
+ 3 lg xs |
s = 0; 1; : : : |
|||
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
1 |
|
||
’.®. 1 = 3:487 2 = 2:267 |
|
|
|
s |
|
xs |
|
|
xs |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
3,5 |
|
|
2,2 |
|
|
|
||
|
|
|
|
|
|
|
1 |
|
3,479 |
|
2,259 |
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
3,481 |
|
2,260 |
|
|
|
|||
|
|
|
|
|
|
|
3 |
|
3,484 |
|
2,261 |
|
|
|
|||
|
|
|
|
|
|
|
4 |
|
3,486 |
|
2,261 |
|
|
|
|||
|
|
|
|
|
|
|
5 |
|
3,487 |
|
2,262 |
|
|
|
|||
|
|
|
|
|
|
|
6 |
|
3,487 |
|
2,262 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…᫨ § ¤ - â®ç-®áâì - 宦¤¥-¨ï ª®à-¥©, â® á«¥¤ã¥â ®£à -¨ç¨¢ âì ¨â¥à 樮--ë© ¯à®æ¥áá, ¥á«¨ ¢ë¯®«-¥-® ãá«®¢¨¥ ( ).
5.3. Œ¥â®¤ •ìîâ®- .
•ãáâì ¨§¢¥áâ-® -¥ª®â®à®¥ ¯à¨¡«¨¦¥-¨¥ x(s) ª ª®à-î á¨á⥬ë ãà ¢-¥-¨© f(x) = 0. ’®£¤ á¯à ¢¥¤«¨¢ § ¯¨áì:
f(x(s) + x(s)) = 0; £¤¥ x(s) = , x(s) |
(1) |
• §« £ ï ãà ¢-¥-¨ï (1) ¢ àï¤ë ¨ ®£à -¨ç¨¢ ïáì ¯¥à¢ë¬¨ ¤¨ää¥à¥-æ¨ « ¬¨, ¯®-
«ã稬: |
|
|
n |
|
|
|
|
fk(x(s)) + |
@fk (x(s)) xi(s) = 0; |
k = 1; : : : ; n |
|
||||
|
|
|
X |
@xi |
|
|
|
|
|
|
i=1 |
|
|
|
|
Žâáî¤ ¯®«ã稬: |
|
|
|
|
|
|
|
n @fk |
|
|
(s) |
= ,fk(x(s)); |
|
|
|
X |
@xi |
(x(s)) xi |
k = 1; : : : ; n |
(2) |
|||
i=1 |
|
|
|
|
|
|
|
‘¨á⥬ ãà ¢-¥-¨©, «¨-¥©- ®â-®á¨â¥«ì-® ª®íää¨æ¨¥-⮢ ¯à¨à é¥-¨ï x(is), ¯à¨ í⮬ ¢á¥ ª®íää¨æ¨¥-âë í⮩ á¨á⥬ë, â ª¦¥ ᢮¡®¤-ë¥ ç«¥-ë ¢ëà ¦ îâáï ç¥à¥§
¯®á«¥¤ãî騥 ¯à¨¡«¨¦¥-¨ï x(s). •¥è¨¢ (2) ª ª¨¬-«¨¡® ¬¥â®¤®¬, - ¯à¨¬¥à ¬¥â®¤®¬ ƒ ãáá , - ©¤¥¬ ¯à¨à é¥-¨¥ x(is), § ⥬, -®¢®¥ s+1 ¯à¨¡«¨¦¥-¨¥ - ©¤¥¬ ¯® ä®à¬ã«¥:
x(s+1) = x(s) + x(is); s = 0; 1; : : :
’¥®à¥â¨ç¥áª¨ - «¨§ á室¨¬®á⨠¬¥â®¤ ¬®¦-® ¯à®¢¥áâ¨, ¥á«¨ ᢥá⨠¬¥â®¤ •ìîâ®- ª ¬¥â®¤ã ¨â¥à 権 ¨ ¢®á¯®«ì§®¢ âìáï ⥮à¥â¨ç¥áª¨¬¨ १ã«ìâ â ¬¨ ¯®- á«¥¤-¥£®. „«ï í⮣® á«¥¤ã¥â ¯®«®¦¨âì
'(x) = x , @f !,1 f(x) @x n n
26
§¤¥áì @f@x ,m1 n{ ¬ âà¨æ , ®¡à â- ï ¬ âà¨æ¥ ¯à®¨§¢¥¤¥-¨ï.
Ž¤- ª®, ¤®áâ â®ç-®¥ ãá«®¢¨¥ á室¨¬®áâ¨, § ¯¨á --®¥ ¢ ª®®à¤¨- â-®© ä®à¬¥, ¯à¨-¨¬ ¥â - á⮫쪮 á«®¦-ë© ¢¨¤, çâ® ¯à®¢¥à¨âì ¥£® ¢ë¯®«-¥-¨¥ ¯®ç⨠-¨ª®£¤ -¥ 㤠¥âáï. •® ¢ ¤®áâ â®ç-® ¬ «®© ®ªà¥áâ-®á⨠ª®à-ï ¨â¥à 樨 á室ïâáï, ¥á«¨
det |
|
@f |
|
= 0, ¯à¨ í⮬ á室¨¬®áâì ¡ã¤¥â ª¢ ¤à â¨ç- ï. ‘«¥¤®¢ ⥫ì-®, ¥á«¨ |
||||||
|
|
|
||||||||
|
@x m n 6 |
|
|
|
|
|
|
|||
-ã«¥¢®¥ ¯à¨¡«¨¦¥-¨¥ ¢ë¡à -® 㤠ç-®, â® ¬¥â®¤ •ìîâ®- á室¨âáï ®ç¥-ì ¡ëáâà® |
||||||||||
(§ |
3{5 ¨â¥à 権), ¯®í⮬㠥£® ¯à¥¤¯®ç¨â î⠨ᯮ«ì§®¢ âì - |
¯à ªâ¨ª¥. ‚ ®â«¨ç¨¨ |
||||||||
®â ¬¥â®¤ |
¨â¥à 権 ¤«ï ¬¥â®¤ |
•ìîâ®- |
å®à®è¨¬ ªà¨â¥à¨¥¬ ®ª®-ç -¨ï ¨â¥à 権 |
|||||||
ï¥âáï ãá«®¢¨¥: |
|
|
|
|
|
|
||||
|
|
|
|
|
kx(s+1) , x(s)k " |
(3) |
||||
|
¢ëç¨á«¥-¨ï ¯® ¬¥â®¤ã •ìîâ®- |
á«®¦-¥¥, 祬 ¯® ¬¥â®¤ã ¨â¥à 権. |
||||||||
•à¨¬¥à 12. Œ¥â®¤®¬ •ìîâ®- |
- ©â¨ ¯®«®¦¨â¥«ì-ë¥ ª®à-¨ á¨á⥬ë: |
|||||||||
|
|
|
|
f1(x1; x2) |
|
2x2 |
x1x2 |
, |
5x1 + 1 = 0 |
|
|
|
|
|
|
1 , |
|
2 |
|
||
|
|
|
|
f2(x1; x2) |
|
x1 + 3 lg x1 , x2 = 0 |
|
|||
•¥è¥-¨¥.
Šà¨¢ë¥ f1(x1; x2) = 0 ¨ f2(x1; x2) = 0 ¯¥à¥á¥ª îâáï ¯à¨¡«¨§¨â¥«ì-® ¢ â®çª å (1; 4; ,1; 5) ¨ (3; 4; 2; 2). ‡ - ç «ì-®¥ ¯à¨¡«¨¦¥-¨¥ ¯à¨¬¥¬ x0 = (3; 4; 2; 2). ˆ¬¥¥¬:
f(x) = |
f1(x1; x2) |
! |
|
f1(x1; x2) |
|||
|
|||
• 室¨¬: |
|
|
|
f(x0) = ,0; 3600 |
! |
||
|
0; 1544 |
||
‘®áâ ¢¨¬ ¬ âà¨æã
|
|
@f1 |
|
@f1 |
@f |
B |
@x1 |
|
@x2 |
@x !2 2 |
|
|
|
|
= 0 |
@f2 |
|
@f2 |
|
|
@ |
@x1 |
|
@x2 |
|
= |
4x1 |
x2 |
5 |
|
|
x1 |
! |
||
C |
|
, |
3M, |
|
, |
|
||||
|
1 + x1 |
|
, |
2x2 |
||||||
1 |
|
|
|
|||||||
A |
|
|
|
|
|
|
|
|
|
|
@f |
(x0)!2 2 |
|
6; 4 |
3; 4 |
! |
@x |
= |
1; 3832 |
,4; 4 |
||
|
|
|
|
, |
|
= det @f@x(x0)! = ,23; 4571 ‘¨á⥬ã (2) à¥è¨¬ ¬¥â®¤®¬ ®¡à â-ëå ¬ âà¨æ, ⮣¤
xs = , @f@x (xs)!,1 |
f(xs) |
||
|
2 2 |
|
|
á«¥¤®¢ ⥫ì-® |
|
|
|
xs+1 = xs + xs = xs , |
@f@x |
(xs)!,1 |
|
|
|
|
2 2 |
27
‚ëç¨á«¨¬ ®¡à â-ãî ¬ âà¨æ㠯ਠ- ç «ì-®¬ ¯à¨¡«¨¦¥-¨¨
|
|
|
@f |
(x0) |
! |
= |
1 |
|
,4; 4 |
3; 4 |
|
|
|
|
|
|
|
|
|
|
|
6; 4 ! |
|
|
|
|
|||||
|
|
|
@x |
|
|
|
|
,1; 3832 |
|
|
|
|
|||
⮣¤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 = |
3; 4 |
|
1 |
|
|
,4; 4 |
|
3; 4 |
,0; 3600 |
|
= |
3; 4899 |
|
||
|
! , 23; 4571 |
|
|
6; 4 ! |
! |
|
! |
||||||||
|
2; 2 |
,1; 3832 |
0; 1544 |
|
2; 26330 |
||||||||||
€- «®£¨ç-® - 室¨¬ ¯®á«¥¤ãî騥 ¯à¨¡«¨¦¥-¨ï:
s xs |
xs |
xs |
xs |
|
|
1 |
1 |
2 |
2 |
0 |
3,4 |
0,0899 |
2,2 |
0,0633 |
1 |
3,4899 |
-0,0008 |
2,2633 |
0,0012 |
2 |
3,4891 |
-1,0016 2,2621 -0,0005 |
||
3 |
3,4875 |
|
2,2616 |
|
…᫨ ®áâ -®¢¨âìáï - ¯à¨¡«¨¦¥-¨¨ x3, â® ¯®«ã稬:
1 x13 = 3; 4875 |
2 x23 = 2; 2616 |
||
f(x3) = |
0; 0000 |
! |
|
0; 0002 |
|||
|
|||
6. €¯¯à®ªá¨¬ æ¨ï äã-ªæ¨©.
6.1. •à¨¡«¨¦¥-¨¥ äã-ªæ¨©.
…᫨ § ¤ - äã-ªæ¨ï y(x) { íâ® ®§- ç ¥â, çâ® «î¡®¥ ¤®¯®«-¨â¥«ì-®¥ §- ç¥-¨¥ x ᮯ®áâ ¢«¥-® §- ç¥-¨î y. •® -¥à¥¤ª® ®ª §ë¢ ¥âáï, çâ® - 宦¤¥-¨¥ í⮣® §- ç¥- -¨ï äã-ªæ¨¨ ®ç¥-ì âà㤮¥¬ª®, ª ¯à¨¬¥àã y(x) ¬®¦¥â ¡ëâì ®¯à¥¤¥«¥-® ª ª à¥è¥-¨¥ á«®¦-®© § ¤ ç¨, £¤¥ x ¨£à ¥â à®«ì ¯ à ¬¥âà , ¨«¨ y(x) ¬®¦¥â ¡ëâì ¨§¬¥-¥- ¢ ¤®à®- £®áâ®ï饬 íªá¯¥à¨¬¥-â¥.
Ž¤- ª®, ¯à ªâ¨ç¥áª¨ ¢á¥£¤ 㤠¥âáï ¢ëç¨á«¨âì -¥¡®«ìèãî â ¡«¨æã §- ç¥-¨© äã-ªæ¨¨, ¢ â® ¢à¥¬ï ª ª ¯àאַ¥ - 宦¤¥-¨¥ äã-ªæ¨¨ ¯à¨ ¡®«ì讬 ç¨á«¥ §- ç¥-¨© à£ã¬¥-â ¯à ªâ¨ç¥áª¨ -¥¢®§¬®¦-®.
”ã-ªæ¨ï y(x) ¬®¦¥â ãç á⢮¢ âì ¢ ª ª¨å-«¨¡® à áç¥â å, £¤¥ ¥¥ ¯à¨å®¤¨âáï ¢ë- ç¨á«ïâì ¯à¨ à §-ëå §- ç¥-¨ïå à£ã¬¥-â . •®í⮬㠮ç¥-ì ç áâ® ¢ë£®¤-® § ¬¥-ïâì äã-ªæ¨î y(x) -¥ª®â®à®© äã-ªæ¨¥© '(x), ª®â®à ï ¡ã¤¥â ¢ -¥ª®â®à®¬ á¬ëá«¥ ¡«¨§ª ª äã-ªæ¨¨ y(x) ¨ ¢ â® ¦¥ ¢à¥¬ï ¯à®áâ® ¢ëç¨á«ï¥âáï, § ⥬ ¯à¨ ¢á¥å x ¯®« £ îâ y(x) '(x). •«¨§®áâì '(x) ª y(x) ¤®á⨣ ¥âáï ¢¢¥¤¥-¨¥¬ ¢ ¯¯à®ªá¨¬¨à®¢ --ãî '(x) ᢮¡®¤-ëå ¯ à ¬¥â஢ a = (a1; : : : ; an) ¨ ¨å ᮮ⢥âáâ¢ãî騬 ¢ë¡®à®¬. Š ª ¯à ¢¨«®, ®¯à¥¤¥«¥-¨¥ - ¨¬¥-ì襣® §- ç¥-¨ï ¯ à ¬¥âà ®áãé¥á⢫ï¥âáï áâ -¤ àâ- -묨 ¯à¨¥¬ ¬¨.
28
6.2.‹¨-¥©- ï ¨-â¥à¯®«ïæ¨ï. •¥¯®á।á⢥--®¥ ¯®áâ஥- -¨¥ ¨-â¥à¯®«ï樮--®£® ¬-®£®ç«¥- .
•ãáâì ¨§¢¥áâ-ë §- ç¥-¨ï äã-ªæ¨© y(x) ¢ -¥ª®â®àëå â®çª å, â.¥. äã-ªæ¨ï y(x) § ¤ - â ¡«¨ç-®:
y(xi) = yi |
i = 1; : : : ; n |
…᫨ ¯®âॡ®¢ âì, çâ®¡ë ¯¯à®ªá¨¬¨à®¢ -- ï äã-ªæ¨ï '(x; a) ᮢ¯ ¤ « á â - |
|
¡«¨ç-ë¬ §- ç¥-¨¥¬ äã-ªæ¨¨ y(x) ¢ n ¢ë¡à --ëå â®çª å, â® ¯®«ã稬 á¨á⥬ã ãà ¢- -¥-¨©:
'(xi; a1; : : : ; an) = yi i = 1; : : : ; n (1)
ˆ§ á¨á⥬ë (1) ¬®¦-® ®¯à¥¤¥«¨âì ¯ à ¬¥âàë a1; : : : ; an. ‚ १ã«ìâ ⥠¯®áâ஥-¨ï äã-ªæ¨ï '(x; a1; : : : ; an) ¡ã¤¥â ¯à¨¡«¨¦ âì äã-ªæ¨î y(x), â.¥. ¡ã¤¥¬ áç¨â âì y(x) '(x).
“ª § --ë© á¯®á®¡ ¯®áâ஥-¨ï ¯¯à®ªá¨¬¨à®¢ --®© äã-ªæ¨¨ - §ë¢ ¥âáï ¨-â¥à- ¯®«¨à®¢ -¨¥¬ ¨«¨ ¨-â¥à¯®«ï樥©. ’®çª¨ xi - §ë¢ îâáï 㧫 ¬¨ ¨-â¥à¯®«ï樨. …᫨ äã-ªæ¨ï ' -¥ «¨-¥©-® § ¢¨á¨¬ ®â ¯ à ¬¥â஢ a1; : : : ; an, â® ¨-â¥à¯®«ïæ¨ï - §ë¢ ¥â- áï -¥«¨-¥©-®©. ‚ í⮬ á«ãç ¥ - 宦¤¥-¨¥ ª®íää¨æ¨¥-⮢ a1; : : : ; an ¬®¦¥â ®ª § âìáï
âàã¤-®© § ¤ 祩 (â.ª. - ¤® à¥è âì á¨á⥬ã -¥«¨-¥©-ëå ãà ¢-¥-¨©). |
|
||
• ¯à ªâ¨ª¥ - ¨¡®«¥¥ à á¯à®áâà -¥- á«ãç © «¨-¥©-®© ¨-â¥à¯®«ï樨, ª®£¤ |
' Ǭ- |
||
-¥©-® § ¢¨á¨¬® ®â a1; : : : ; an, â.¥. ¯à¥¤áâ ¢¨¬ |
¢ ¢¨¤¥ â ª - §ë¢ ¥¬®£® ®¡®¡é¥--®£® |
||
¬-®£®ç«¥- : |
n |
|
|
|
|
|
|
'(x; a1; : : : ; an) = |
X |
ak'k(xi) |
(2) |
k=1
Žç¥¢¨¤-® 'k(x) ¬®¦-® áç¨â âì «¨-¥©-® -¥§ ¢¨á¨¬®©, ¨- ç¥ ç¨á«® ç«¥-®¢ ¢ á㬬¥, , §- ç¨â, ¨ ¯ à ¬¥â஢ ¬®¦-® ¡ë«® ¡ë 㬥-ìè¨âì.
•®¤áâ ¢¨¬ (2) ¢ (1), ¯®«ã稬 ¤«ï ®¯à¥¤¥«¥-¨ï ¯ à ¬¥â஢ ak б«¥¤гойго б¨бв¥¬г
ãà ¢-¥-¨©:
n
|
X |
ak'k(xi) = yi |
|
|
i = 1; : : : ; n |
(3) |
||
|
k=1 |
|
|
|
|
|
|
|
‘¨á⥬ |
(3) ¯à¥¤áâ ¢«ï¥â ᮡ®© á¨á⥬㠫¨-¥©-ëå ãà ¢-¥-¨©, ®â-®á¨â¥«ì-® a1; : : : ; an. |
|||||||
—â®¡ë § ¤ ç ¨-â¥à¯®«ï樨 ¢á¥£¤ |
¨¬¥« |
¥¤¨-á⢥--®¥ à¥è¥-¨¥, -ã¦-®, çâ®¡ë ¯à¨ |
||||||
«î¡®¬ à ᯮ«®¦¥-¨¨ 㧫®¢ det (3) ¡ë« ®â«¨ç¥- ®â 0, â.¥. |
|
|||||||
|
'1(x1) '2(x1) : : : 'n(x1) |
|
|
|||||
|
'1(x2) '2(x2) : : : 'n(x2) |
= 0 |
(4) |
|||||
|
. |
. |
.. |
|
. |
|||
|
. |
. |
. |
. |
6 |
|
||
|
. |
. |
|
. |
|
|||
|
'1(xn) '2(xn) : : : 'n(xn) |
|
|
|||||
‘¨á⥬ |
äã-ªæ¨©, 㤮¢«¥â¢®àïîé ï âॡ®¢ -¨ï¬ (4) - §ë¢ « áì 祡ë襢᪮©. |
|||||||
„«ï «¨-¥©-®© ¨-â¥à¯®«ï樨 - ¨¡®«¥¥ 㤮¡-® ¢ ª ç¥á⢥ äã-ªæ¨© 'k(x) ¢ë¡¨à âì ®¡ëç-ë¥ ¬-®£®ç«¥-ë. ’¥à¬¨- "¨-â¥à¯®«ïæ¨ï" ¢ 㧪®¬ á¬ëá«¥ 㯮âॡ«ïîâ ⮣¤ , ¥á«¨ x § ª«îç¥-® ¬¥¦¤ã ªà ©-¨¬¨ 㧫 ¬¨ ¨-â¥à¯®«ï樨. …᫨ x ¢ë室¨â § 㪠- § --ë¥ ¯à¥¤¥«ë, â® £®¢®àïâ ®¡ íªáâà ¯®«ï樨.
29

7. ˆ-â¥à¯®«ï樮--ë© ¬-®£®ç«¥- ‹ £à -¦ .
•ãáâì ¤ -ë n + 1 à §«¨ç-ëå §- ç¥-¨© |
à£ã¬¥-â |
x0; x1; : : : ; xn ¨ ¨§¢¥áâ-ë ¤«ï |
||||||||
äã-ªæ¨¨ y = y(x) ᮮ⢥âáâ¢ãî騥 §- ç¥-¨ï y(xi) = yi. |
|
|||||||||
•®áâந¬ ¬-®£®ç«¥- Ln(x) á⥯¥-¨ -¥ ¢ëè¥ n: Ln(xi) = yi |
i = 0; : : : ; n |
|||||||||
‚롥६ ¢ ª ç¥á⢥ 'k(x) = xk |
|
k |
= 0; : : : ; n |
⮣¤ á¨á⥬ ãà ¢-¥-¨© (3) |
||||||
¯à¨¬¥â ¢¨¤: |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
akxik = yi |
|
|
i = 0; : : : ; n |
(5) |
||||
|
k=0 |
|
|
|
|
|
|
|
|
|
det (5) { ¥áâì ®¯à¥¤¥«¨â¥«ì ‚ -¤¥à¬®-¤ . |
|
|
|
|
||||||
|
1 |
x0 |
x2 |
: : : |
xn |
|
|
|
||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
1 |
x1 |
x2 |
: : : |
xn |
|
|
|
||
|
. . |
.1 . |
. |
|
.1 |
= = 0 |
|
|||
|
. . . |
. |
. |
|
6 |
|
||||
|
. . . |
|
|
. |
|
|
||||
|
1 |
xn |
x2 |
: : : |
xn |
|
|
|
||
|
|
n |
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
||
‘¨á⥬ ¨¬¥¥â ¥¤¨-á⢥--®¥ à¥è¥-¨¥, ⥬ á ¬ë¬ ¬ë ¤®ª § «¨ áãé¥á⢮¢ -¨¥ ¨ |
||
¥¤¨-á⢥--®áâì ¨-â¥à¯®«ï樮--®£® ¬-®£®ç«¥- : |
|
|
n |
|
|
X |
akxk |
(6) |
k=0 |
|
|
•®«ã稬 ï¢-®¥ ¯à¥¤áâ ¢«¥-¨¥ ¨-â¥à¯®«ï樮--®£® ¬-®£®ç«¥- (6) -¥ ¯à¨¡¥£ ï -¥¯®- á।á⢥--® ª à¥è¥-¨î (5)
‘- ç « |
¯®áâந¬ ¬-®£®ç«¥- á⥯¥-¨ n |
Pk(x) â ª®©, çâ® Pk(xi) = ki, £¤¥ ki { |
|
ᨬ¢®« Šà®-¥ª¥à |
|
|
|
|
1; k = i |
|
|
|
ki = 0; |
k = i |
(7) |
|
|
6 |
|
’.ª. Pk(x) ®¡à é ¥âáï ¢ -ã«ì ¢ n â®çª å x0; x1; : : : ; xk,1; xk+1; : : : ; xn, â® ¡ã¤¥¬ ¨áª âì |
|||
¥£® ¢ ¢¨¤¥ |
|
|
|
|
Pk(x) = ck(x , x0)(x , x1) : : : (x , xk,1)(x , xk+1) : : : (x , xn) |
(8) |
|
£¤¥ ck { ¯®áâ®ï--ë© ª®íää¨æ¨¥-â. |
|
|
|
‚ (8) ¯®«®¦¨¬ x = xk ¨ ãç⥬, çâ® Pk(xk) = 1. ‚ १ã«ìâ ⥠- 室¨¬ ck |
= |
||
(xk , x0)(xk |
, x1) : : : (xk , xk,1)(xk , xk+1) : : : (xk , xn). ’.®. ¯®áâந«¨ ¬-®£®ç«¥- |
||
Pk(x) ¢ ¢¨¤¥ |
|
|
|
Pk(x) = (x , x0)(x , x1) : : : (x , xk,1)(x , xk+1) : : : (x , xn) (xk , x0)(xk , x1) : : : (xk , xk,1)(xk , xk+1) : : : (xk , xn)
’¥¯¥àì ¯®áâந¬ ¬-®£®ç«¥- Ln(x):
n
Ln(x) = X ykPk(x)
k=0
(9)
(10)
„¥©á⢨⥫ì-®, ¬-®£®ç«¥- Ln(x) ¨§ (10) ¨ (9), ¨¬¥¥¬ á⥯¥-ì -¥ ¢ëè¥ n. Šà®¬¥ ⮣®, - ®á-®¢ -¨¨ (7) ¯®«ãç ¥¬:
n
Ln(xi) = X ykPk(xi) = yiPi(xi) = yi
k=0
30
