
Часть 2 Теория
.pdf
Часть 2. Элементы качественной теории дифференциальных уравнений и теории нелинейных колебаний
1.Автономные системы
1.1.Свойства решений автономных систем
Везде ниже независимую переменную будем обозначать через t и трактовать ее как время. Неизвестные функции будем обозначать x1(t), x2 (t),..., xn (t).
Система дифференциальных уравнений называется автономной (динамической), если независимая переменная не входит явным обра-
зом в систему. Общий вид динамической системы в Rn следующий:
|
|
dxi |
= f |
i |
(x , x |
2 |
,..., x |
n |
), i = 1, 2, K, n ; |
(1.1.1) |
||
|
|
|
|
|||||||||
|
|
dt |
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
или в векторной записи: |
|
|
|
|
|
|
|
|
||||
|
dx |
|
|
|
x Rn |
|
|
(1.1.1') |
||||
|
|
= f (x), |
|
|
||||||||
|
dt |
|
|
|||||||||
Будем предполагать, что в некоторой области G Rn |
все функ- |
|||||||||||
ции fi (x1, x2 ,..., xn ) |
непрерывны вместе со своими частными произ- |
|||||||||||
водными ∂fi . Таким образом, в области G × (− ∞, ∞) выполнены все
∂x j
условия теоремы Коши.
Установим некоторые свойства решений автономных систем.
1) Если x = ϕ(t) – решение системы (1.1.1'), то для произвольного C=const вектор-функция ϕ(t + C) также является решением этой системы.
Справедливость приведенного утверждения сразу вытекает из со-
отношений
dϕ(t + C) |
= |
dϕ(t + C) |
= f [ϕ(t + C)]. |
|
dt |
d(t + C) |
|||
|
|
Если x = ϕ(t) – решение системы (1.1.1' ), определенное на неко- тором множестве t T , то множество γ = {x : x = ϕ(t),t T} представ-
ляет собой кривую в Rn . Эту кривую называют «фазовой траектори- ей» системы (1.1.1'). Множество фазовых траекторий системы обра-
зует ее «фазовый портрет» в «фазовом пространстве» Rn .
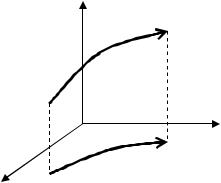
Заметим, что фазовая траектория представляет собой проекцию интегральной кривой x = ϕ(t), заданной в Rn+1, в пространство Rn в направлении, параллельном оси t.
t x=ϕ(t)
γ
x2
Рис. 1.1.1
χ(t) = ϕ(t). Значит
|
2) Две фазовые траектории либо не |
||||
|
имеют общих точек, либо совпадают. |
||||
t |
Пусть γ1 и γ 2 – две фазовые траек- |
||||
|
тории, отвечающие решениям |
x = ϕ(t) |
|||
|
и x =ψ (t), имеют общую точку x0 . |
То- |
|||
x1 |
гда |
ϕ(t1) = x0 =ψ (t2 ) . |
Пусть |
||
|
χ(t) =ψ[t + (t2 − t1 )]. |
По свойству |
1) |
||
|
χ(t) есть решение системы (1.1.1'). Но |
||||
|
χ(t1) = ψ (t2 ) = ϕ(t1) . |
Поэтому, в силу |
|||
|
свойства |
единственности |
решения, |
||
ϕ(t) =ψ[t + (t2 − t1 )]. То есть кривые γ1 и γ 2 сов-
падают.
Определение 1.1.1. Точка a называется положением равновесия системы (1.1.1') (точкой покоя, особой точкой, сингулярной точкой),
если f(a)=0.
3) |
Если a – положение равновесия системы (1.1.1'), то |
||||
x(t) ≡ a (−∞ < t < ∞) - решение этой системы. |
|||||
В самом деле: 0 = |
da |
= |
dx |
= f (x(t)) = f (a) = 0. |
|
dt |
|
||||
|
|
|
dt |
||
4) |
Всякая фазовая траектория, отличная от точки покоя, явля- |
||||
ется гладкой кривой, (то есть имеет в любой своей точке ненулевой касательный вектор).
Действительно, в точке x0 |
= ϕ(t0 ) имеем x&(t0 ) = |
dϕ(t0 ) |
= f (x0 ) ¹ 0 . |
|
dt |
||||
|
|
|
Справедливо следующее утверждение.
Теорема 1.1.1. Всякая фазовая траектория автономной системы принадлежит к одному из трех типов:
а) гладкая кривая без самопересечений;
b)замкнутая гладкая кривая (цикл);
c)точка.
В доказательстве нуждается только утверждение b) теоремы. Для простоты рассуждений будем считать, что все решения системы опре- делены на интервале (−∞, ∞) . Пусть x(t, x0 ) (x(0, x0 ) = x0 ) – решение,
не являющееся положением равновесия. Пусть фазовая траектория этого решения пересекает сама себя, то есть существуют такие значе- ния t1 и t2 , что x(t1, x0 ) = x(t2 , x0 ). Поскольку x0 не положение рав- новесия, то можем считать, что x(t, x0 ) ¹ x(t1, x0 ) при t Î(t1,t2 ). По- ложим ω = t2 - t1 и покажем, что x(t, x0 ) – ω -периодическая функция.
По доказанному выше ~x(t) = x(t + ω, x0 ) также является решением си-
стемы, причем:
~x(t1 ) = x[t1 + (t2 - t1), x0 ] = x(t2 , x0 ) = x(t1, x0 ).
По теореме единственности ~x(t) º x(t, x0 ) Þ x(t, x0 ) º x(t + ω, x0 ). Итак, решение x(t, x0 ) – ω -периодическое. Фазовая траектория
такого решения, очевидно, замкнутая кривая (цикл).
5) |
Пусть x(t, x0 ) (x(0, x0 ) = x0 ) – решение автономной системы. |
Тогда |
x(t1 + t2 , x0 ) = x(t1, x(t2 , x0 )) = x(t2, x(t1, x0 )) (для решений вы- |
полнено групповое свойство).
Доказательство справедливости этого утверждения проводится так: очевидно функции ϕ1 (t) = x(t, x(t1, x0 )) и ϕ2 (t) = x(t + t1, x0 ) так-
же являются решениями |
системы. |
При этом |
ϕ1(0) = x(t1, x0 ) , |
ϕ2 (0) = x(t1, x0 ). В силу |
теоремы единственности |
ϕ1(t) º ϕ2 (t) Þ |
|
Þ ϕ1(t2 ) = ϕ2 (t2 ) Þ x(t2, x(t1, x0 )) = x(t1 + t2 , x0 ).
Заметим, что из доказанного свойства фазовых траекторий авто-
номной системы вытекает, что |
x(-t, x(t, x0 )) = x0 . |
|||
1.2. Фазовая плоскость линейной системы второго порядка |
||||
Рассмотрим линейную однородную систему второго порядка с |
||||
постоянными вещественными коэффициентами |
||||
|
dx |
|
= a |
x + a y |
|
|
|||
|
dt |
11 |
12 |
|
|
|
|
(1.2.1) |
|
|
dy |
|
|
|
|
|
= a21x + a22 y |
||
|
dt |
|
||
Пусть x = ϕ(t), y =ψ (t) – вещественные решения системы (1.2.1). |
||||
Тогда уравнения |
|
|
|
|
ìx = ϕ(t), |
t Î(-¥, ¥) |
|||
í |
|
|
|
|
îy =ψ (t), |
|
|||
определяют фазовую траектория системы (1.2.1). Очевидно, что точка (0,0) – положение равновесия системы.
Так как система (1.2.1) интегрируется, то можно построить ее фа- зовый портрет. Пусть λ1, λ2 – собственные значения матрицы A = (aij ) системы (1.2.1). Могут представиться два случая
а) корни λ1, λ2 вещественны, б) корни λ1, λ2 комплексно-сопряженные числа.
Мы рассмотрим ниже только так называемый основной случай. Основной случай. Собственные значения матрицы А различны и
отличны от нуля. В этом случае качественная картина расположения фазовых траекторий (фазовый портрет системы) не меняется при малых изменениях ее коэффициентов.
Предположим сначала, что оба собственных значения веществен-
ны. Тогда решение системы (1.2.1) имеет вид: |
|
||||||||
æ xö |
|
|
+ C |
|
eλ2t e |
|
, |
(1.2.2) |
|
ç |
÷ = C eλ1t e |
2 |
2 |
||||||
ç |
÷ |
1 |
1 |
|
|
|
|
||
è yø |
|
|
|
|
|
|
|
|
|
где C1,C2 – произвольные постоянные, а e1, e2 – собственные векто- ры, соответствующие собственным значениям λ1, λ2 . Пусть ξ1,ξ2 ко-
|
|
æ xö |
|
|
|
|
|
. Тогда |
|
|
ординаты вектора ç |
÷ в базисе e , e |
2 |
|
|||||||
|
|
ç |
÷ |
|
1 |
|
|
|
||
|
|
è yø |
|
|
|
|
|
|
|
|
ξ |
1 |
= C eλ1t , ξ |
2 |
= C |
2 |
eλ2t . |
(1.2.3) |
|||
|
|
1 |
|
|
|
|
|
|||
Поскольку в силу (1.2.3) фазовый портрет симметричен относительно начала координат, то достаточно построить его только в первом квад- ранте (C1 ³ 0,C2 ³ 0). Рассмотрим несколько случаев.
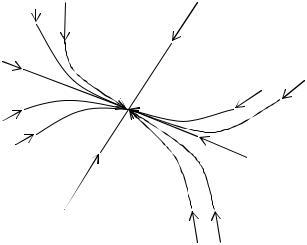
I.Числа λ1, λ2 одного знака.
x2 |
1) λ1 < 0, λ2 < 0 . |
Тогда |
при |
|||
C1 = 0, |
C2 = 0 получаем точку |
|||||
|
||||||
|
покоя |
(0,0). Если |
C1 > 0,C2 = 0, |
|||
0 |
то фазовая траектория – ось ξ1. |
|||||
Если |
C1 = 0,C2 > 0 – ось |
ξ2 . |
||||
|
Стрелки на рис.1.2.1 показывают |
|||||
x1 |
направление, в котором движется |
|||||
точка |
по |
фазовой |
траектории с |
|||
|
ростом t. |
|
|
|
||
|
Если C1 > 0,C2 > 0, то в силу |
|||||
Рис. 1.2.1 |
(1.2.3) |
|
ξ1 ® 0,ξ2 ® 0 |
при |
||
|
t → +∞, |
ξ1 ® ¥, |
ξ2 ® ¥ |
при |
||

|
|
|
|
|
|
|
|
|
ξ2 |
= |
C2 |
e |
(λ −λ )t |
→ 0 |
|
t |
→ −∞ |
. Если |
λ > λ |
2 , |
(| |
λ < λ |
2 |
|) , тогда |
|
|
2 1 |
при |
|||
|
|
||||||||||||||
|
1 |
1 | | |
ξ1 |
|
C1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t → +∞ и фазовые траектории «входят» в точку (0,0) по касательной к оси ξ1. Точка покоя в рассматриваемом случае – устойчивый узел.
2) 0 < λ1 < λ2 . Фазовый портрет точно такой же, как и на рис.1.2.1,
только стрелки направлены от начала координат. Это неустойчивый узел.
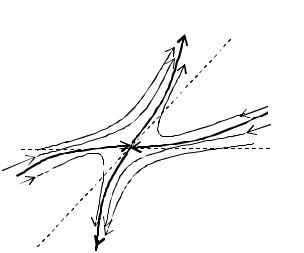
II. Числа λ1, λ2 разных знаков. |
|
|
|
||||||||
Пусть, |
для |
|
определенности, |
λ1 > 0, λ2 < 0. |
При C1 = 0,C2 > 0 |
||||||
имеем: ξ |
1 |
= 0 , ξ |
2 |
= C |
2 |
eλ2t ® 0 при t → +∞. При C > 0,C |
2 |
= 0 имеем |
|||
|
|
|
|
|
|
1 |
|
||||
x2 |
|
|
|
|
|
|
|
ξ2 = 0,ξ1 → ∞ при t → +∞. Если |
|||
|
|
|
|
|
|
|
|
C1 > 0,C2 > 0, то ξ1 → ∞,ξ2 → 0 |
|||
|
|
|
|
|
|
|
|
при t → +∞. |
Получаем картину, |
||
|
|
|
|
|
|
|
|
изображенную схематически на |
|||
|
|
|
|
|
|
|
|
рис.1.2.2. Состояние |
равновесия |
||
|
|
|
0 |
|
|
|
x1 |
(0,0) – седло, |
четыре луча, вхо- |
||
дящие в эту точку и выходящие из нее – усы седла..
Рис. 1.2.2
Случай комплексных собственных значений. Пусть λ и λ –
комплексно-сопряженные собственные значения, а e – собственный вектор, соответствующий собственному значению λ . Тогда можно
выделить два линейно независимых вещественных решения системы
(1.2.1): Re(eλt e )и Im(eλt e ). Если λ = a + bi, e = f1 + if2, то
Re(eλt e )= eat ( f |
|
|
|
|
sin bt), |
Im(eλt e )= eat ( f |
|
|
|
sin bt). |
cosbt - f |
2 |
2 |
cosbt + f |
|||||||
1 |
|
|
|
1 |
||||||
Составив линейную комбинацию выделенных вещественных реше- ний, получим общее решение системы (1.2.1)
æ xö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im(eλt e )= ξ f +ξ |
|
f |
|
|
, |
|||||
ç |
÷ = C Re(eλt e )+ C |
2 |
2 |
2 |
||||||||
ç |
÷ |
1 |
1 1 |
|
|
|
||||||
è yø |
|
|
|
|
|
|
|
|
|
|
|
|
где:
ξ |
1 |
= eat (C cos bt + C |
2 |
sin bt), ξ |
2 |
= eat (C |
2 |
cos bt - C sin bt). |
(1.2.4) |
|
1 |
|
|
1 |
|
Предположим сначала, что собственные значения чисто мнимые:
λ1,2 = ±bi ,

тогда: |
|
|
|
|
|
|
|
|
cos bt - C sin bt) Þ ξ 2 + ξ 2 |
= C 2 |
+ C 2 . |
|||||
ξ |
1 |
= (C |
cos bt + C |
2 |
sin bt), ξ |
2 |
= (C |
2 |
||||||||
|
1 |
|
|
|
|
|
|
1 |
1 |
2 |
1 |
2 |
||||
|
|
x2 |
|
|
|
|
|
|
В |
косоугольной |
системе |
координат |
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
такое уравнение задает, вообще гово- |
|||||||
|
|
|
|
|
|
|
|
|
ря, некоторое семейство эллипсов. |
|||||||
|
|
|
|
|
|
|
x1 |
Состояние равновесия в этом случае |
||||||||
|
|
|
|
|
|
|
называется центром (рис. 1.2.3). |
|
||||||||
|
|
|
центр |
|
|
|
|
|
|
|
Если |
a ¹ 0, |
то, в соответствии с |
|||
|
|
|
|
|
|
|
|
формулой (1.2.4), траектории реше- |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Рис. 1.2.3 |
|
|
|
|
ний системы будут спиралями. При |
||||||||
|
|
|
|
|
|
|
|
|
|
a < 0 они |
закручиваются |
к |
центру. |
|||
Состояние равновесия в этом случае называют устойчивым фокусом. При a > 0 спирали будут раскручиваться от центра. Это случай не-
устойчивого фокуса (рис. 1.2.4).
x2 |
|
x2 |
||
|
|
|
|
|
|
x1 |
|
x1 |
|
|
|
|
|
|
Устойчивый фокус |
Неустойчивый фокус |
Рис. 1.2.4
1.3.Исследование положений равновесия нелинейной системы второго порядка
Рассмотрим нелинейную систему второго порядка: |
|
|||
|
dx |
|
= f1(x, y) |
|
|
dt |
|
||
|
, |
(1.3.1) |
||
|
dy |
|||
|
|
= f2 (x, y) |
|
|
|
dt |
|
|
|
|
|
|
|
|
причем будем предполагать, что функции f1(x, y), f2 (x, y)дважды непрерывно дифференцируемы во всей плоскости XOY.
Положения равновесия (точки покоя) системы (1.3.1) определя- ются как решения системы уравнений:
ì f1 (x0 , y0 ) = 0, íî f2 (x0 , y0 ) = 0.
Так как путем замены переменных ~x = x − x0 , ~y = y − y0 точку покоя (x0 , y0 ) можно всегда перевести в начало координат (0,0) , то
мы будем в дальнейшем считать, что изучаемое положение равнове- сия есть начало координат (0,0).
Линеаризуя систему (1.3.1) в начале координат, то есть разлагая правые части системы в ряды Тейлора по степеням x и y , и отбра-
сывая члены второго и высшего порядков малости, получим линей- ную систему:
|
dx |
|
= a |
x + a y |
|
|
|||
|
dt |
11 |
12 |
|
|
|
|
(1.3.2) |
|
|
dy |
|
|
|
|
|
= a21x + a22 y |
||
|
dt |
|
||
|
|
|
|
|
Пусть λ 1, λ2 – собственные |
значения матрицы A = (aij ) системы |
|||
(1.3.2). Положение равновесия (0,0) будем называть невырожденным, если λ 1¹ λ 2 и Reλ1,2 ¹ 0. Оказывается, что в невырожденном слу-
чае поведение траекторий вблизи положения равновесия (0,0) для нелинейной системы (1.3.1) в существенном совпадает с поведением траекторий линейной системы (1.3.2) вблизи положения равновесия
(0,0).
За положением равновесия (0,0) системы (1.3.1) сохраним те же названия, что и за положением равновесия системы (1.3.2): если λ 1 и
λ 2 вещественны и одного |
знака, то положение равновесия узел |
(λ 1< 0,λ2 < 0 – устойчивый, |
λ 1> 0,λ 2> 0 – неустойчивый). Если λ 1 |
и λ2 комплексно-сопряженные с отрицательными (положительными) вещественными частями, то положение равновесия (0,0) – устойчи- вый (неустойчивый) фокус. Если λ 1 и λ 2 вещественны и разных знаков, то положение равновесия – седло.
Следующие теоремы, которые будут даны без доказательства, определяют поведение траекторий нелинейной системы (1.3.1) вбли-
зи невырожденного положения равновесия (0,0) в зависимости от ти- па точки покоя системы (1.3.2).
Теорема 1.3.1. Предположим, что точка покоя О(0,0) системы (1.3.2) является седлом. Пусть Р – прямая, проходящая через точку О в направлении собственного вектора e1 матрицы A = (aij ) , соот-
ветствующего отрицательному собственному значению λ1, а Q – прямая, проходящая через точку О в направлении собственного век- тора e2 матрицы A = (aij ) , соответствующего положительному
собственному значению λ2 , Тогда существуют ровно две траекто- рии U1 и U 2 системы (1.3.1), которые при t → +∞ асимптотически
приближаются к точке О(0,0). Эти две траектории вместе с точ- кой О образуют непрерывно дифференцируемую кривую, касающую- ся прямой Р в точке О. Точно также существуют ровно две траек- тории V1 и V2 , которые при t → −∞ асимптотически приближают-
ся к точке О, касаясь при этом прямой Q. Остальные траектории в окрестности точки О ведут себя так, как показано на рис.1.3.1.
Q |
Траектории U1 и U 2 – устой- |
|
чивые усы седла, траектории V1 и |
||
V1 |
||
|
V2– неустойчивые усы седла. |
|
U1 |
Теорема 1.3.2. Пусть точка |
|
О(0,0) устойчивый (неустойчи- |
||
О |
вый) узел, то есть λ1 < λ2 < 0 |
|
P |
(0 < λ2 < λ1 ) . В направлении соб- |
|
U2 |
ственного вектора, соответ- |
|
|
ствующего λ2 , проведем через |
|
|
точку О прямую Р, а в направле- |
|
V2 Рис. 1.3.1 |
нии собственного вектора, соот- |
|
|
ветствующего λ1 – прямую Q. |
Оказывается, что все траектории, начинающиеся достаточно близ-
ко от |
точки |
О, асимптотически приближаются при |
t → +∞ |
(t → −∞) |
к точке О и имеют в этой точке касательную. |
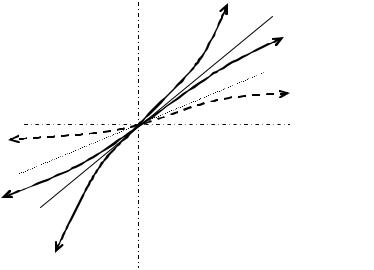
При этом только две траектории входят в точку О по касательной к прямой Q,, а остальные – по касательной к прямой Р (соответ- ственно при t → +∞ и t → −∞) (см. рис. 1.3.2).
P
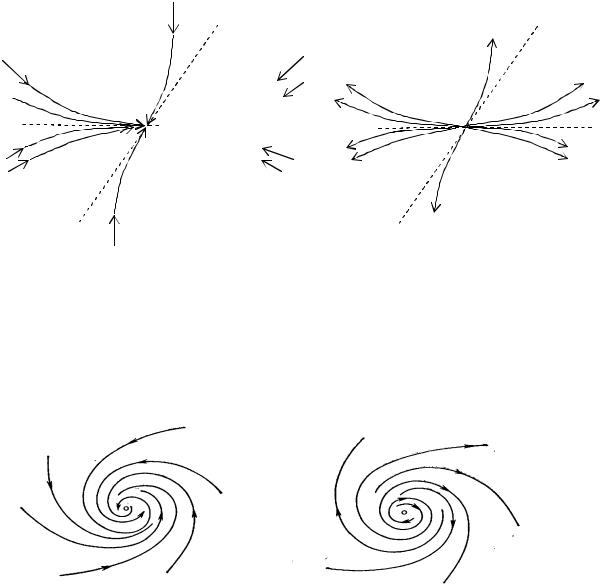
λ1 < λ2 < 0 |
Q |
Q |
|
0 < λ2 < λ1 |
 P
P
Рис. 1.3.2 |
|
|
Теорема 1.3.3. Пусть точка |
О |
– фокус, то есть |
λ1,2 = a ± bi, a ¹ 0, b ¹ 0. Тогда при a < 0 |
все траектории системы |
|
(1.3.1), проходящие вблизи точки О, при t → +∞ наматываются на точку О, а при a > 0 наматываются при t → −∞ на точку О как спирали (см. рис. 1.3.3).
Устойчивый фокус |
Неустойчивый фокус |
|
Рис. 1.3.3 |
Пример 1.3.1. Найти особые точки системы:
ìdx |
|
= 4x2 - y2 , |
|
ï |
|
||
|
(1.3.3) |
||
ídt |
|||
ïdy |
|
= -4x + 2xy - 8, |
|
ï |
|
|
|
î dt |
|
|
|
определить их тип. Построить схематически фазовый портрет в окрестности каждой особой точки.
Решение. Для нахождения особых точек решим систему уравне-
ний
ì4x2 |
- y2 = 0 |
Þ x1 = 2, y1 = 4; x2 = -1, y2 = -2. |
í |
|
|
î- 4x + 2xy - 8 |
= 0 |
|
Итак, особыми будут точки M1(2, 4) и M2(–1,–2).
Разлагая правые части системы в ряды Тейлора в окрестности каждой из особых точек и ограничиваясь только линейными членами этих разложений, получим две линейные системы:
|
ìdx |
= 16x - 8y |
|
|
|
|
|
|||
для точки M1(2, 4): |
ï |
|
|
|
|
|
|
|
||
|
|
|
, |
и |
|
|
|
|
||
ídt |
|
|
|
|
|
|||||
|
ï |
dy |
|
= 4x + 4y |
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
||
|
î dt |
|
|
|
|
|
|
|
||
|
ìdx |
= -8x + 4y |
|
|
|
|
|
|||
для точки M2(–1,–2): |
ï |
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
ídt |
|
|
|
|
|
|
||||
|
ïdy |
= -8x - 2y |
|
|
|
|
|
|||
|
ï |
|
|
|
|
|
|
|
||
|
î dt |
|
æ16 |
− 8ö |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Собственные значения матрицы A = ç |
÷первой из этих систем |
|||||||||
|
|
|
|
1 |
ç |
÷ |
|
|
|
|
|
|
|
|
|
è 4 |
4 ø |
|
|
|
|
|
|
|
|
e2 = (1,1) |
λ1 = 12, λ2 = 8 |
– |
положи- |
|||
|
|
|
|
|
|
тельны, |
поэтому |
особая |
||
|
|
|
|
e1 = (2,1) |
точка |
M1(2, |
4) |
является |
||
|
|
|
|
точкой типа «неустойчи- |
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
вый узел». |
|
|
||
(2,4) |
|
|
|
|
|
Для построения фазового |
||||
|
|
|
|
|
портрета |
в |
окрестности |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
точки |
|
M1(2, |
4) |
найдем |
|
|
|
|
|
|
собственные векторы, со- |
||||
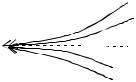
Рис. 1.3.4 |
|
|
ответствующие |
найден- |
||||||
|
|
ным |
собственным значе- |
|||||||
|
|
|
|
|
|
ниям матрицы А1. Имеем: |
||||
e1 = (2, 1), e2 = (1, 1). Согласно теореме 1.3.2, только две траектории выходят из особой точки M1(2, 4) по касательной к направлению, определяемому собственным вектором e1, а остальные выходят из нее по касательной к направлению, определяемому вектором e2
(рис.1.3.4)
