
Часть 2 Теория
.pdf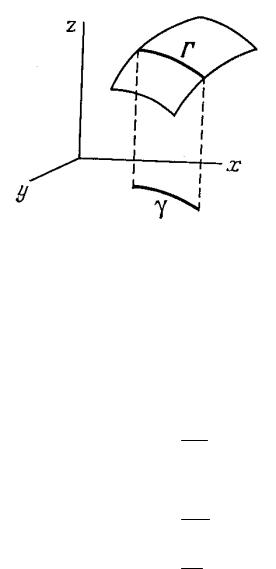
ривать как частный случай квазилинейного уравнения (1.5.11), задача Коши формулируется точно также.
Пусть пространственная кривая Γ задана параметрическими уравнениями x = x(t), y = y(t), z = z(t) . Обозначим через γ проекцию этой кривой на плос-
кость xOy . Задача Коши для уравнения (1.5.4) ставится так: в окрестности кривой γ найти интегральную поверхность уравнения (1.5.4), проходящую че-
рез заданную кривую Γ , т.е. найти такое решение уравнения (1.5.4), которое принимает заданные значения в точках кривой γ .
Задача Коши имеет единственное ре- шение, если кривая Γ не является характе- ристикой уравнения (1.5.4), то есть не явля- ется интегральной системы (1.5.6). Если же Γ – характеристика, то задача Коши имеет бесконечно много решений.
Общее решение линейного и квазилинейного уравнения
Как уже было сказано выше, линейное уравнение с частными производны- ми может рассматриваться как частный случай квазилинейного уравнения. По- этому мы сначала рассмотрим метод решения квазилинейного уравнения, из которого очевидным образом выводится метод решения линейного уравнения.
Покажем, что интегрирование квазилинейного уравнения (1.5.11) сводится
к отысканию первых интегралов системы уравнений характеристик
dxdt1 = a1(x1, x2 ,Kxn ,u),
LLLLLLLLLL
dx (1.5.12) dtn = an (x1, x2 ,Kxn ,u),
dudt = b(x1, x2 ,Kxn ,u)
Будем искать функцию v(x1, x2 ,Kxn ,u) такую, что для решения
u(x1,K, xn ) уравнения (1.5.11) v(x1, x2 ,Kxn ,u(x1,K, xn )) есть первый интеграл системы (1.5.12), то есть, например, v(x1, x2 ,Kxn ,u(x1,K, xn )) ≡ 0 вдоль траек-
торий системы (1.5.12). Из последнего тождества находим

∂u |
|
|
∂v |
|||
= − |
∂xi |
|
. |
|||
|
|
|
||||
∂xi |
|
∂v |
|
|||
|
|
|
∂u |
|||
Подставляя эти соотношения в уравнение (1.5.11), получим
n |
∂v |
|
∂v |
|
|
åai (x1,Kxn ,u) |
+ b(x1,Kxn ,u) |
= 0 . |
|||
|
∂u |
||||
i=1 |
∂xi |
|
|||
(1.5.13)
Уравнение (1.5.13) имеет тот же вид, что и уравнение (1.5.3) (уравнение (1.4.5)). Согласно теореме 1.4.2 всякое решение уравнения (1.5.11) есть функция от n независимых первых интегралов v j (x1, x2 ,Kxn ,u), j =1,2,Kn системы (1.5.12),
то есть имеет вид v(x1, x2 ,Kxn ,u) = Φ[v1(x1, x2 ,Kxn ,u),K,vn (x1, x2 ,Kxn ,u)]. По-
этому решение уравнения (1.5.11) в неявном виде записывается так: Φ[v1(x1, x2 ,Kxn ,u),K,vn (x1, x2 ,Kxn ,u)] = 0.
(1.5.14)
Замечание 1. Если функция u входит только в один из первых интегралов vj (x1, x2 ,Kxn ,u) , например в vn (x1, x2 ,Kxn ,u) , то решение уравнения (1.5.11)
может быть записано в виде vn (x1, x2 ,Kxn ,u) = ϕ(v1,v2 ,K,vn−1) , где ϕ – произ- вольная дифференцируемая функция. Разрешив последнее уравнение относи- тельно u , получим общее решение в явном виде.
Замечание 2. В случае линейного однородного уравнения (1.5.3) из тео- ремы 1.4.2 сразу следует, что общее решение этого уравнения имеет вид
u(x1,Kxn ) = Φ(u1(x1,Kxn ),u2 (x1,Kxn ),K,un−1(x1,Kxn )),
(1.5.15)
где ui (x1,K, xn ),i =1,2,K,n −1– независимые первые интегралы системы харак-
теристик
|
dx1 |
= a1(x1, x2 ,Kxn ), |
|
|
dt |
(1.5.16) |
|
|
|
||
LLLLLLLLLL |
|||
dxdtn = an (x1, x2 ,Kxn ),
а Φ(.,K,.) – произвольная дифференцируемая функция n −1 переменных.
Пример 1. Найти общее решение уравнения (x + 2y) ∂∂xz − y ∂∂yz = 0
Решение. Это линейное уравнение. Составим систему характеристик
(1.5.16)

dxdt = x + 2y
dydt = -y
Для нахождения первого интеграла исключим из этой системы dt . Приходим к
соотношению
dx |
= |
dy |
Þ ydx + (x + 2y)dy = 0 . |
|
x + 2y |
- y |
|||
|
|
Получили уравнение в полных дифференциалах. Его общее решение легко находится и имеет вид xy + y2 = C . Левая часть последнего равенства является первым интегралом системы, поэтому, согласно замечанию 2, общее решение
исходного уравнения |
|
имеет вид z = ϕ(xy + y2 ) , где ϕ(×)– произвольная диффе- |
||||||||||||||||||||||||||
ренцируемая функция. |
|
|
|
|
|
|
∂z |
|
∂z |
|
||||||||||||||||||
Пример 2. Найти общее решение уравнения ex |
+ y2 |
= yex . |
||||||||||||||||||||||||||
|
¶y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
|||||
Решение. Данное уравнение имеет вид (1.5.11), поэтому система характе- |
||||||||||||||||||||||||||||
ристик для него имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
dx |
|
= ex , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dy |
|
= y2 , |
|
|
Þ |
dx |
= |
dy |
= |
dz |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dt |
|
|
|
|
|
|
|
yex |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
ex |
|
y2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dz |
|
= yex , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из уравнения |
dx |
= |
dy |
находим один первый интеграл |
|
1 |
- e−x = C . Учиты- |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ex |
|
|
y2 |
|
|
|
|
|
|
|
|
|
y |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вая, что ex = |
|
|
y |
|
из уравнения |
dy |
= |
dz |
находим еще один первый инте- |
|||||||||||||||||||
1 |
- yC |
|
yex |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
грал z - |
ln | y | −x |
= C2 . Согласно формуле (1.5.14), общий интеграл уравнения |
||||||||||||||
|
||||||||||||||||
|
e−x - y−1 |
|
ln | y | −x |
|
|
|
|
|
|
|
||||||
имеет вид F(y |
−1 - e−x , z - |
) = 0. Пользуясь замечанием 1, общее реше- |
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
e−x - y−1 |
|
|
|
|||||||
ние уравнения можем записать в виде z = |
ln | y | −x |
+ f ( |
1 |
- e−x ). |
||||||||||||
e−x - y−1 |
|
|||||||||||||||
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
y |
||||
Решить уравнение |
|
|
|
|||||||||||||
|
|
|
x2 |
∂u |
+ y2 |
∂u |
+ z2 |
∂u |
= u |
|
|
|
||||
|
|
|
¶x |
¶y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
¶z |
|
|
|
|||||

Решение. Уравнение является квазилинейным. Запишем уравнение для ха- рактеристик (см. (1.5.5))
dxx2 = dyy2 = dzz2 = duu .
Из этих уравнений находим три независимых первых интеграла
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|
||
- |
= C , |
- |
= C |
, ue |
x |
= C |
. |
|||||
|
|
|
|
|||||||||
x |
y |
1 |
x |
|
z |
2 |
|
|
3 |
|
||
|
|
|
|
|
|
|
||||||
Так как функция u входит только в последний интеграл, то согласно замеча- нию 1, общее решение уравнения может быть записано в виде
1 |
æ 1 |
|
1 |
|
1 |
|
1 |
ö |
− |
1 |
æ 1 |
|
1 |
|
1 |
|
1 |
ö |
|||
|
|
|
|
|
|
|
|
|
|||||||||||||
ue x |
= ϕç |
|
- |
|
, |
|
- |
|
÷ Þ u = e |
|
xϕç |
|
- |
|
, |
|
- |
|
÷, |
||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ç |
|
|
|
|
x |
|
z |
÷ |
|
|
ç |
|
|
|
|
x |
|
z |
÷ |
|
|
è x y |
|
|
ø |
|
|
è x y |
|
|
ø |
||||||||||
где ϕ – некоторая непрерывно дифференцируемая функция своих переменных.
Решение задачи Коши
Изложим без доказательства метод решения задачи Коши для квазилиней- ного уравнения (1.5.4). В силу приведенных выше рассуждений, этот метод применим и для решения линейного уравнения, то есть в случае, когда функции a,b,c не зависят от переменной z .
Итак, пусть требуется найти интегральную поверхность уравнения (1.5.4), проходящую через кривую Γ , заданную параметрическими уравнениями
|
x = x(t), y = y(t), z = z(t) . |
(1.5.17) |
|||||
Пусть найдены два независимых первых интеграла системы |
|
||||||
|
dx |
= |
dy |
= |
dz |
|
|
|
|
|
|
: |
|
||
|
a(x, y, z) |
b(x, y, z) |
c(x, y, z) |
|
|||
|
f1(x, y.z) = C1, f1(x, y.z) = C1. |
(1.5.18) |
|||||
Выразив x, y, z через параметр t из соотношений (1.5.17) и подставив эти вы- ражения в (1.5.18), получим два соотношения вида F1(t)= C1, F2 (t)= C2 . Исклю- чив t из последних соотношений, получим выражение вида Φ(C1,C2 ) = 0 . Под- ставив в это выражение вместо C1 и C2 левые части первых интегралов (1.5.18), получим искомое уравнение интегральной поверхности, которое и бу-
дет решением поставленной задачи Коши. |
|
|
|
|||||
Замечание |
3. |
Часто |
кривая |
Γ |
задается |
соотношениями |
||
ψ1(x, y, z) = 0,ψ 2 (x, y, z) = 0 . |
В |
этом случае |
в |
качестве параметра на кривой |
||||
можно выбрать |
x |
или |
y . |
Иначе говоря, |
для получения соотношения |
|||
Φ(C1,C2 ) = 0 нужно исключить переменные x, y, z из системы уравнений |
||||||||
|
|
|
|
ìψ1(x, y, z) = 0, |
|
|||
|
|
|
|
ï |
|
|
|
|
|
|
|
|
ïψ 2 (x, y, z) = 0, |
(1.5.19) |
|||
|
|
|
|
í f |
(x, y.z) = C , . |
|||
|
|
|
|
ï 1 |
|
|
1 |
|
|
|
|
|
ï f |
(x, y.z) = C |
|
||
|
|
|
|
î 1 |
|
|
1 |
|

|
|
Пример 4. Найти решение задачи Коши x |
∂z + y |
∂z |
|
=1. z = x при y =1. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
¶y |
|
|
|
|
|
Решение. Запишем систему уравнений характеристик |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= dy = dz . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
1 |
|
|
|
|
|
|
|||||
|
|
Найдем независимые первые интегралы этой системы: |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
dx |
= dy |
Þ |
|
y |
= C , dy |
= dz |
Þ z - ln y = C |
|
, |
|
||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
x |
|
1 |
|
y |
1 |
|
|
|
|
2 |
|
|
||||||||||
(здесь мы пишем ln y , |
а не ln | y | , поскольку решение ищется в окрестности |
||||||||||||||||||||||||||||||||
плоскости |
y =1). Исключив переменные x, y, z из соотношений |
z = x , y =1, |
|||||||||||||||||||||||||||||||
|
y |
= C , z − ln y = C |
2 |
, |
получим C |
2 |
= |
1 |
|
. Подставив в последнее равенства вместо |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
C1,C2 левые части выражение для первых интегралов, окончательно будем |
|||||||||||||||||||||||||||||||||
иметь |
z - ln y = |
x |
|
Þ z = |
x |
+ ln y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пример 5. Найти поверхность, удовлетворяющую данному уравнению и |
|||||||||||||||||||||||||||||||
проходящую через данную линию. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
y |
∂z - x ∂z = y2 |
- x2 |
, z = |
|
1 |
|
, x = 0 . |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
y2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
¶x |
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решение. Запишем систему уравнений характеристик |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= |
|
dy |
|
= |
|
dz |
|
(= t). |
|
|
|
(1.5.20) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
- x |
y2 - x2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Из соотношения dx = |
dy |
|
|
легко находится первый интеграл |
x2 + y2 = C . |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
- x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Чтобы найти еще один первый интеграл, воспользуемся известным свойством
пропорций: если |
a1 |
= |
a2 |
=L |
am |
= t , то при любых p1, p2 ,Kpm справедливо ра- |
b |
b |
|
||||
|
|
|
b |
|||
|
1 |
2 |
|
m |
||
венство p1a1 + p2a2 + Lpmam = t . Пользуясь приведенным свойством, из соот- |
||
p1b1 + pb2 + Lpmbm |
||
ношений (1.5.20) получим |
||
ydx + xdy = |
dz |
Þ d(xy) = dz Þ xy - z = C2 . |
y2 - x2 |
y2 - x2 |
|
Теперь запишем систему (1.5.19) для данной задачи и исключим из нее пе- ременные x, y, z :

ìx = 0, |
|
|||
ï |
|
1 |
|
|
ï |
|
, |
||
|
|
2 |
||
ïz = |
y |
|||
í |
|
|
|
|
ïx2 |
+ y2 = C , |
|||
ï |
|
|
|
1 |
ï |
|
|
|
= C2 |
îxy - z |
||||
ìy |
2 = C1, |
|
1 |
|
||||
ï |
|
|
|
|
Þ C1 + |
|
||
Þ í |
1 |
= C2 |
|
= 0 . |
||||
C2 |
||||||||
ï- |
|
|
|
|
|
|||
|
y |
2 |
|
|
||||
î |
|
|
|
|
|
|
||
Подставив вместо C1 и C2 левые части выражений для первых интегралов,
после элементарных преобразований окончательно получим искомое уравнение
поверхности: z = xy + 1 . x2 + y2
IIТеория устойчивости
2.1Понятие устойчивости по Ляпунову
Слово устойчивость настолько выразительно, что правильные интуитивные представления об устой-
|
2 |
чивости имеются у всех. |
|
|
|||
|
|
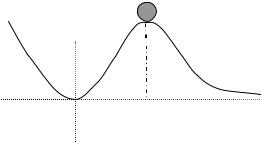
Рассмотрим |
металлический |
ша- |
|||
1 |
|
рик, |
который |
катается |
по |
горке |
|
|
(рис.2.1.1). Имеются две точки покоя |
||||||
О |
~ |
|
~ |
|
|
|
|
x = 0 и x = x (дно впадины 1 и вер- |
|||||||
|
x |
||||||
|
Рис. 2.1.1 |
шина горки 2). Ясно, что первое из |
|||||
|
них устойчиво, а второе – |
нет. В са- |
|||||
|
|
мом |
деле, если |
поместить |
шарик в |
||
точку 1 и слегка толкнуть, то он начнет совершать незатухающие (при отсутствии трения) колебания вокруг этой точки. Если же толк- нуть шарик, помещенный на вершину горки 2, то он или скатится во впадину, или укатится на ∞.
Но таких наглядных представлений об устойчивости абсолютно недостаточно для решения мало-мальски серьезной задачи об устой- чивости реальной физической или технической системы.
Теория устойчивости создавалась многими математиками, меха- никами, физиками. Фундаментальные результаты по теории устойчи- вости принадлежат знаменитому русскому математику А.М. Ляпуно-
ву (1857 – 1918). |
|
Рассмотрим систему |
|
x& = f (t, x), x Rn |
(2.1.1) |
Через x(t,t0 , x0 ) будем обозначать решение этой системы с началь-
ным условием x(t0 ,t0 , x0 ) = x0 .
Определение 2.1.1. Решение η(t, a, x0 ) системы (2.1.1) называ-
ется устойчивым по Ляпунову, если оно определено при всех t ³ a и для произвольных ε > 0 и t0 Î(a, ¥) можно указать такое δ (ε,t0 ),
что:
1) все решения x(t,t0 , y0 ) , удовлетворяющие условию
|η(t0 , a, x0 ) - x(t0 ,t0 , y0 ) |< δ
определены при "t ³ t0 ;
2) для этих решений справедливо неравенство
|η(t, a, x0 ) − x(t,t0 , y0 ) |< ε при t [t0 ,∞) .
Определение 2.1.2. Решение η(t, a, x0 ) называется асимптоти- чески устойчивым по Ляпунову, если оно устойчиво по Ляпунову и
lim |η(t, a, x0 ) − x(t,t0 , y0 ) |= 0.
t→∞
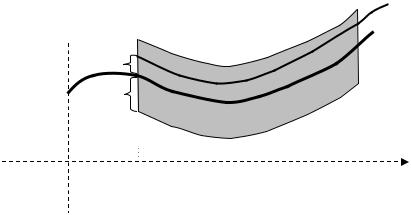
Иными словами, решение η(t, a, x0 ) устойчиво, если достаточно близкое к нему в любой начальный момент решение x(t,t0 , y0 ) цели-
ком погружается в сколь угодно узкую ε- трубку, построенную во-
круг η(t, a, x0 ) (рис.2.1.2).
x(t,t0 , y0 )
|
δ |
η(t, a, x0 ) |
|
} |
|
|
ε |
|
|
|
|
а |
t0 |
t |
Рис. 2.1.2
В дальнейшем мы будем в основном рассматривать автономные системы
x& = f (x), |
x Rn ,( f (a) = 0) |
(2.1.2) |
и исследовать устойчивость их положений равновесия. |
|
|
Определение 2.1.3. |
Положение равновесия x = a |
системы |
(2.1.2) называется устойчивым по Ляпунову, если для любого ε > 0 можно указать δ = δ (ε) > 0 такое, что:
1)если | x0 − a |< δ , то решение x(t, x0 ) системы (2.1.2) опреде- лено при всех t ³ 0 ;
2)при всех t [0,∞) выполнено условие | x(t, x0 ) − a |< ε .
Если к тому же lim | x(t, x0 ) − a |= 0 , то состояние равновесия
t→∞
x = a асимптотически устойчиво по Ляпунову.
В рассмотренном выше примере с шариком, положение равнове- сия 1 устойчиво по Ляпунову (но не асимптотически). Если же нали-
чествует трение, то это положение равновесия асимптотически устойчиво.
Ранее нами была рассмотрена линейная автономная система вто- рого порядка с постоянными коэффициентами. Начало координат (0,0) – положение равновесия. Его устойчивость, по сути дела, уже исследована. Можно утверждать, что устойчивый узел и устойчивый фокус – асимптотически устойчивые положения равновесия; центр – устойчивое по Ляпунову, но не асимптотически устойчивое положе- ние равновесия; седло и неустойчивый узел – неустойчивые положе- ния равновесия.
2.2 Общие теоремы об устойчивости линейных систем
Рассмотрим линейную систему |
|
||
|
dy |
= A(t)y + f (t), |
(2.2.3) |
|
|
||
|
dt |
|
|
где A(t) − n × n матрица, f(t) – n-вектор, |
y(t) – n -вектор. Будем счи- |
||
тать, что все элементы матрицы A(t) и все компоненты вектор- функции f(t) непрерывны при t (−∞,∞). Наряду с системой (2.2.3)
будем рассматривать линейную однородную систему
|
dx |
= A(t)x, x Rn . |
(2.2.4) |
|
dt |
||
Определение 2.2.1. Линейную систему (2.2.3) |
будем называть |
||
устойчивой (вполне неустойчивой), если все ее решения устойчивы (неустойчивы) по Ляпунову при t → +∞.
Замечание 2.2.1. Как будет ясно из дальнейшего, решения линей- ных систем либо все одновременно устойчивы, либо неустойчивы. Подобная терминология неприменима к нелинейным системам, не- которые решения которых могут быть устойчива, тогда как другие
– неустойчивы.
Теорема 2.2.1. Для устойчивости линейной системы (2.2.3) при любом свободном члене f(t) необходимо и достаточно, чтобы было устойчиво тривиальное решение x(t) ≡ 0 (t0 < t < ∞,t0 (−∞,∞)) со-
ответствующей однородной системы (2.2.4).
Доказательство. Необходимость. Пусть η(t) (t0 ≤ t < ∞) – ка-
кое-либо устойчивое решение системы (2.2.3). Это значит, что для произвольного ε > 0 найдется δ > 0 такое, что для произвольного решения y(t) этой системы из условия
| y(t0 ) -η(t0 ) |< δ |
(2.2.5) |
следует, что |
|
| y(t) −η(t) |< ε при "t ³ t0 |
(2.2.6) |
Но x(t) = y(t) −η(t) – решение однородной системы (2.2.4), причем любое ее решение x(t) может быть представлено в таком виде. Отсю- да, из соотношений (2.2.5) и (2.2.6) и определения устойчивости сле- дует, что x(t) ≡ 0 – устойчивое решение системы (2.2.4).
Замечание 2.2.2. Из приведенных рассуждений следует, что устойчивость решения x(t) ≡ 0 системы (2.2.4) вытекает из устой- чивости хотя бы одного решения системы (2.2.3) при каком-либо значении f(t) (например, при f (t) ≡ 0).
Достаточность. Пусть решение x(t) ≡ 0 системы (2.2.4) устой- чиво по Ляпунову при t → +∞. Тогда если x(t) (t0 £ t < ¥) – какое- либо решение однородной системы и | x(t0 ) |£ δ (ε,t0 ), то | x(t) |< ε
при t Î[t0 ,¥) . Значит если | y(t0 ) -η(t0 ) |< δ для любых двух реше- ний системы (2.2.3), то | y(t) −η(t) |< ε при t Î[t0 ,¥) . Следовательно,
η(t) – устойчивое при t → +∞ решение. Теорема доказана.
Следствие 2.2.1. Линейная система (2.2.3) устойчива, если устойчиво хотя бы одно ее решение и вполне неустойчива, если не- устойчиво некоторое ее решение.
Справедливость утверждения следствия вытекает из теоремы
2.2.1 и замечания 2.2.2.
Следствие 2.2.2. Система (2.2.3) устойчива тогда и только то- гда, когда устойчива однородная система (2.2.4).
Следствие 2.2.2 в совокупности с теоремой 2.2.1 показывает, что
можно ограничиться только изучением устойчивости тривиального решения x(t) ≡ 0 однородной системы (2.2.4).
Определение 2.2.5. Линейную систему (2.2.3) будем называть асимптотически устойчивой, если любое ее решение y(t) асимпто-
тически устойчиво при t → +∞.
Теорема 2.2.2. Система (2.2.3) асимптотически устойчива то- гда и только тогда, когда асимптотически устойчиво решение x(t) ≡ 0 однородной системы (2.2.4).
