
Часть 2 Теория
.pdf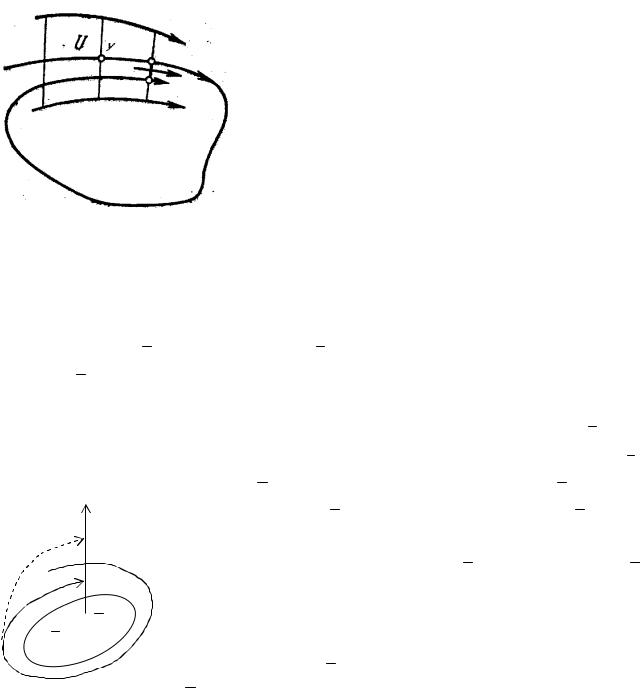
Пусть у не является точкой покоя. Рассмотрим малую окрест- ность U точки у. Причем будем считать, что окрестность U ограни- чена двумя отрезками нормалей к части дуги γ , содержащей точку у,
и двумя дугами траекторий системы (рис. 3.1.2). Совокупность тра- екторий в U имеет вид мало искривленного семейства параллельных отрезков. Поскольку у является ω - предельной точкой траектории γ ,
то при увеличении t траектория γ должна вновь пересечь U. Пока- жем, что при этом траектория γ вновь пройдет через точку y. Это и
s Мешок
Бендиксона
Рис.3.1.2
будет означать, что γ – замкнутая кривая. Если это не так, то траектория γ ,
пройдя через окрестность U "ниже точки у", попадет в замкнутую область S ("мешок Бендиксона"), которую она больше не сможет покинуть при возрастании t и, зна- чит, она больше не сможет приблизиться к точке у (рис. 3.1.2).
Аналогичная ситуация возникает в том случае, когда γ пересекает окрестность U "выше точки y". Теорема доказана.
Лемма 3.1.1. Пусть γ – положительная полутраектория реше- ния x(t) системы (3.1.1), имеющая ω -предельную точку, принадле- жащую циклу γ . Тогда либо γ = γ , либо γ спиралевидно приближа- ется к γ при t ® +¥.
Доказательство. Поскольку множество ω -предельных точек полутраектории γ состоит из целых траекторий, любая точка γ так-
же является
nx
d c
a
 x
x
γ
Рис. 3.1.3
ω -предельной точкой полутраектории γ . Пусть x γ . Пусть nx – малый отрезок нормали к γ , прохо- дящий через x . В силу того, что x – ω - предельная точка полутраектории γ , эта полутра-
|
ектория пересекает отрезок nx |
в окрестности |
x |
||||
|
бесконечное число раз. Пусть |
с и а– две последо- |
|||||
|
вательные точки пересечения. Если, с = a то γ – |
||||||
γ |
замкнутая траектория. Если |
c ¹ a , то расстояние |
|||||
от точки а до |
x |
меньше, чем расстояние от c до |
|||||
|
|||||||
x (рис. 3.1.3). Если бы это было не так (пунктир

на рисунке 3.1.3), то образовался бы "мешок", ограниченный отрез- ком dc и частью γ , в который не может войти γ с ростом t. По- следнее приводит к противоречию с предположением, что x – ω - предельная точка полутраектории γ .
Итак, если γ не является циклом, то последовательные точки пе- ресечения γ с nx сходятся к x . Но тогда из непрерывной зависимо- сти от начальных данных вытекает, что γ навивается на γ .
Теорема 3.1.2. Пусть некоторая полутраектория γ системы
(3.1.1) содержится в замкнутом ограниченном множестве G R2 , в котором нет точек покоя этой системы. Тогда эта полутраекто- рия либо является циклом, либо навивается на цикл системы (3.1.1)
при t → +∞.
Доказательство. Поскольку полутраектория γ |
x |
ограничена, мно- |
жество ее ω -предельных точек не пусто. Пусть |
– какая-либо ω - |
предельная точка полутраектории γ . Если x γ , то по теореме 3.1.1 γ – цикл. Пусть x γ . Рассмотрим траекторию γ , проходящую че-
рез x . Эта траектория также ограничена (она содержится в G ) и по- тому множество ее ω -предельных точек не пусто. Пусть x – ω -
предельная точка траектории γ |
. Докажем, что |
|
|
γ |
|
. Тогда из теоре- |
|||||||||||||||||
x |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
a |
мы 3.1.1. будет следовать, что γ |
– цикл, а из леммы |
||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
3.3.1 – что γ навивается на γ |
|
|
при t → +∞. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
Предположим, что |
|
γ |
|
. |
|
|
Рассмотрим малую |
|||||||||
|
|
|
|
|
|
|
x |
|
|
||||||||||||||
|
γ |
|
|
c |
|
|
|
|
|||||||||||||||
|
|
|
окрестность точки |
|
и нормаль к γ |
, проходящую |
|||||||||||||||||
|
|
|
|
|
|
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
через эту точку (рис. 3.1.4). Пусть выбранная нор- |
||||||||||||||||
|
|
|
|
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
маль пересекается всеми траекториями системы
γ(3.1.1) вовнутрь "мешка", образованного отрезком
ac и частью траектории γ . Так как все точки траек- тории γ являются ω -предельными для γ , то γ бу- дет в какой-либо момент близка к точке c, и потому она попадет в
"мешок". Но тогда во все последующие моменты времени γ будет находиться внутри "мешка", и потому она не сможет больше прибли- зиться к точке a, которая также является ω -предельной для γ . Итак, x γ . Доказательство теоремы завершено.
Замечание 3.1.1. Все сформулированные выше утверждения остаются справедливыми, если в них заменить t на (-t) и ω - предельные точки на α -предельные.
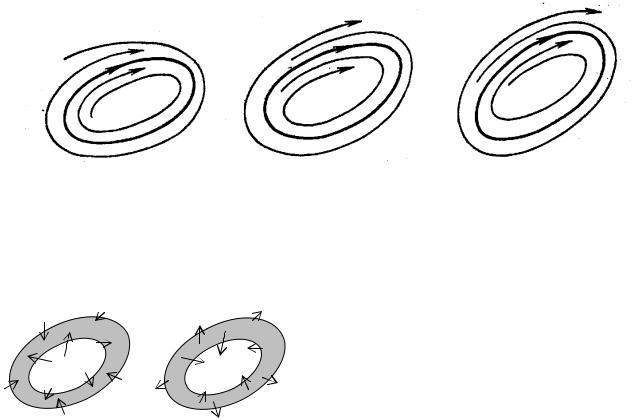
Возможные типы поведения траекторий в окрестности цикла
Если двумерная система имеет изолированный цикл (то есть та- кой, в достаточно малой окрестности которого нет других циклов), то он может быть одного из следующих типов: устойчивый цикл (все траектории системы из достаточно малой окрестности цикла наматы- ваются на него при t → +∞ как изнутри, так и снаружи), неустойчи- вый цикл (все траектории системы из достаточно малой окрестности цикла наматываются на него при t → −∞ как изнутри, так и снаружи), полуустойчивый цикл (траектории из достаточно малой окрестности цикла наматываются на него изнутри при t → +∞ и снаружи при t → −∞, или наоборот).
Все приведенные здесь утверждения мы оставляем без доказа- тельства. Их доказательства могут быть проведены по той же схеме, которая была применена при доказательстве теорем 3.1.1 и 3.1.2 и леммы 3.1.1. Соответствующие картинки даны на рис. 3.1.5.
Устойчивый цикл |
Неустойчивый цикл Полуустойчивый |
|
цикл |
|
Рис. 3.1.5 |
|
Принцип кольца |
Положитель- |
Отрицательно |
но инвариант- |
инвариантная |
ная область |
область |
Рис. 3.1.6.
Пусть на плоскости имеется замкнутая кольцеобразная об- ласть, ограниченная двумя за- мкнутыми гладкими кривыми γ1 и γ2 (γ1 и γ2 не являются траектори- ями системы (3.1.1)!) , такая, что все траектории системы (3.1.1)
входят вовнутрь этой области с ростом t и в дальнейшем не поки-
дают ее (или входят в эту область при убывании t и не покидают ее при t → −∞). Такая область называется положительно (отрицатель- но) инвариантной для траекторий системы (рис. 3.1.6).
Лемма 3.1.2. Если внутри положительно (отрицательно) инва- риантной для траекторий системы (3.1.1) области нет состояний равновесия системы, то в этой области содержится по крайней мере один цикл системы (3.1.1).
Справедливость утверждений леммы 3.1.2 немедленно вытекает из теоремы 3.1.2 и замечания к ней.
Существование циклов у систем с единственным положением равновесия
Пусть x = 0– единственное состояние равновесия системы (3.1.1). Пусть все собственные значения матрицы Якоби:
æ |
∂f |
1 |
|
|
∂f |
1 |
ö |
ç |
|
|
|
|
÷ |
||
¶x1 |
|
¶x2 |
|||||
J (x) = ç |
|
÷ |
|||||
ç |
¶f2 |
|
¶f2 |
÷ |
|||
ç |
|
|
|
|
÷ |
||
¶x |
|
|
¶x |
2 |
|||
è |
|
1 |
|
|
|
ø |
|
при x1 = 0, x2 |
= 0 |
имеют положительные вещественные части. Тогда |
|||||
рассматриваемая точка будет состоянием равновесия типа неустой-
чивый узел или неустойчивый фокус. В обоих случаях у системы
(3.1.1) нет траекторий, приближающихся к точке покоя при t → +∞. Значит состояние равновесия системы (3.1.1) не может быть ω - предельной точкой ни для одной ограниченной при t ³ 0 полутраек- тории этой системы.
Предположим, что система (3.1.1) является диссипативной. То- гда все ее положительные полутраектории ограничены. Из приведен- ных рассуждений и теоремы 3.1.2 вытекает справедливость следую- щего утверждения.
Теорема 3.1.3. Если все собственные значения матрицы Якоби J (x) системы (2.8.1) при x = 0 имеют положительные веществен-
ные части и система диссипативна, то она имеет по крайней мере один цикл.
Проиллюстрируем на примерах применение леммы 3.1.2 и теоре- мы 3.1.3 для доказательства существования циклов.
Пример 3.1.1. Доказать, что уравнение &x&+ (x2 + x&2 -1)x& + x = 0 имеет цикл.
Решение. Положим x = x1 , x& = x2 |
и запишем данное уравнение в |
|||||||||||
виде эквивалентной системы в R2 : |
|
|
|
|
|
|
||||||
ìx& |
= x |
|
, |
|
|
|
|
|
|
|
(3.1.2) |
|
í 1 |
|
2 |
|
|
|
|
|
|
|
|
||
îx&2 = -(x12 + x22 -1)x2 - x1. |
Рассмотрим |
функцию |
v(x1, x2 ) = |
|||||||||
|
|
|
x12 + x22 = 0.5 |
|
||||||||
|
|
|
|
= x12 + x22 . |
Ее производная в |
силу |
||||||
|
|
|
|
|
|
системы |
(3.1.2) |
имеет |
вид |
|||
|
|
|
|
|
|
v& = 2x2 (1 - x2 |
- x2 ). |
Рассмотрим |
||||
|
|
|
|
|
|
две |
2 |
1 |
2 |
окружности |
||
|
|
|
|
|
|
концентрические |
||||||
|
|
|
|
|
|
x2 + x2 = 0.5 |
и x2 + x2 |
= 2. |
На |
|||
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
x2 |
+ x2 = |
2 |
первой из них выполнено условие |
||||||
|
|
|
v& > 0, а на второй v& < 0. Поэтому |
|||||||||
|
|
|
1 |
2 |
|
|||||||
Рис. 3.1.7. |
|
|
траектории |
системы |
пересекают |
|||||||
|
|
|
|
|
|
первую окружность по |
направле- |
|||||
нию "от центра", а вторую – по направлению "к центру". Значит в фа-
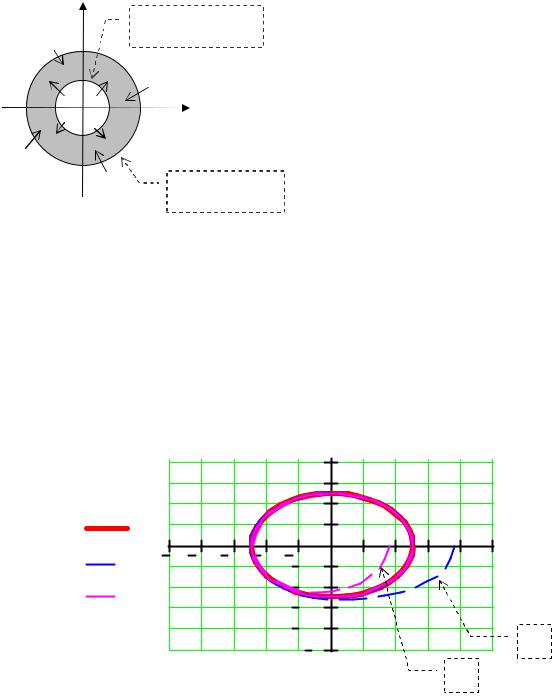
зовом пространстве рассматриваемой системы имеется положительно инвариантное кольцо (рис. 3.1.7). Согласно лемме 3.1.2, такая система имеет цикл.
На приведенном ниже рис. 3.1.8. изображен цикл системы (3.1.2), найденный путем численного интегрирования, а также траектории, навивающиеся на этот цикл при t → +∞ изнутри и снаружи.
|
|
|
|
|
1.6 |
|
|
|
|
|
|
|
|
|
|
|
1.2 |
|
|
|
|
|
|
X1 n ,3 |
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
X2 n ,3 |
2 |
1.6 |
1.2 |
0.8 |
0.4 |
0 |
0.4 |
0.8 |
1.2 |
1.6 |
2 |
X3 n ,3 |
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1.2 |
|
|
|
|
|
|
|
|
|
|
|
1.6 |
|
|
|
|
X2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 n ,2 , |
X2 n ,2 , X3 n ,2 |
|
X3 |
|
|||
|
|
|
|
|
|
|
|||||
Рис. 3.1.8.
Пример 3.1.2. Доказать, что уравнение
&x&+ [1 + (x - 2)e−x2 ]x& + x = 0

имеет цикл.
Отбросив в разложении функции e−x2 в ряд Тейлора члены, со-
держащие x в степени 2 и выше (e−x2 =1 - x2 + x4
2!
линеаризованное в точке x = 0 уравнение &x&− x& + x = 0. Оба корня со- ответствующего характеристического уравнения имеют положитель- ные вещественные части.
Перепишем исходное уравнение в виде &x&+ x& + x + + (x - 2)e−x2 x& = 0. Характеристический полином линейной части это-
го уравнения ( p2 |
+ p +1) гурвицев, а интеграл от коэффициента при |
|
x |
2 dt ), |
|
x& ( ò (t - 2)e−t |
как это легко проверить, равномерно ограничен |
|
0 |
|
|
при всех x (0, ∞) . Поэтому, по теореме 2.8.2, соответствующая дан-
ному уравнению система второго порядка является диссипативной. Значит, согласно теореме 3.1.3, рассматриваемое уравнение имеет пе- риодическое решение (цикл).
Пример 3.1.3. Доказать, что система
ì |
|
|
|
−(x2 + y2 ) |
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
íx& = -x + 2y + 4xe |
|
|
|
|
|
||||
ï |
|
|
|
|
|
|
|
|
|
îy& = -3x - y |
|
|
|
|
|
|
|||
имеет цикл. |
линеаризованной в точке x = 0, y = 0 системы |
||||||||
Здесь |
матрица |
||||||||
æ |
3 |
2 |
ö |
|
|
2 |
+ y |
2 |
) ограничена, |
A = ç |
|
|
÷ антигурвицева. Так как функция 4xe−(x |
|
|
||||
ç |
- 3 |
|
÷ |
|
|
|
|
|
|
è |
-1ø |
|
|
|
|
|
|
||
|
|
|
æ −1 |
2 ö |
|
|
|
|
|
а матрица B = ç |
|
÷ гурвицева, то по теореме 2.8.1 система дис- |
|||||||
|
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
è- 3 |
-1ø |
|
|
|
|
|
сипативна. Согласно теореме 3.1.3, рассматриваемая система имеет цикл.
3.2Метод Пуанкаре в теории нелинейных колебаний. Неавтономные уравнения
Метод Пуанкаре предназначен для построения периодических решений нелинейных систем, дифференциальные уравнения которых содержат малый параметр μ. При этом предполагается, что обраще- ние в нуль малого параметра не понижает порядка системы.
Метод Пуанкаре базируется на двух положениях:
1)порождающая система, т.е. система, получающаяся из исход- ной при μ=0, содержит периодические решения с некоторым перио- дом, частным случаем которых могут быть постоянные величины;
2)периодические решения исходной системы строятся при по- мощи подбора начальных данных всех входящих в систему неиз- вестных функций.
Начнем с решения следующей задачи: требуется найти периоди- ческое решение периода T дифференциального уравнения:
&x&+ ω 2 x = f (t) |
(3.2.1) |
Заметим, что если решение уравнения (3.2.1) |
имеет период T, то |
x(t + T ) º x(t) Þ &x&(t) + ω 2 x(t) = f (t + T ), то есть функция f(t) обязана быть периодической с периодом T. Выполнив в (3.2.1) замену време-
|
|
|
|
2π |
|
|
|
|
|
|
|
|
æ t T |
ö |
|
|
|
|
||
ни t |
1 |
= |
|
|
t и положив f |
1 |
(t ) = |
f ç |
1 |
÷, получим |
|
|
||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
T |
|
|
|
|
1 |
|
|
è 2π ø |
|
|
|
|
||||||
|
|
|
|
|
|
|
(t + 2π )T ö |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
æ |
|
|
æ t T |
ö |
|
|
|
||||||
f |
1 |
(t + |
2π ) = |
f ç |
1 |
|
|
÷ |
= |
f ç |
1 |
|
+ T ÷ |
= f (t + T ) = f (t) = f |
1 |
(t ). |
||||
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
è |
2π |
ø |
|
|
è 2π |
ø |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
То есть новая правая часть в новом времени будет 2π-периодической функцией. Поэтому правую часть уравнения (3.2.1) можно без огра- ничения общности считать 2π-периодической функцией.
Будем считать, что функция f(t) непрерывна и может быть разло-
жена в сходящийся ряд Фурье
|
a0 |
∞ |
|
|
f (t) = |
+ å(ak cos kt + bk sin kt) |
(3.2.2) |
||
|
||||
2 |
k=1 |
|
||
Пользуясь принципом суперпозиции, частное решение уравнения (3.2.1) будем искать в виде ряда
|
A0 |
∞ |
|
|
|
|
|
x(t) = |
+ å(A |
cos kt + B |
k |
sin kt) |
(3.2.3) |
||
|
|||||||
2 |
k |
|
|
|
|||
k=1 |
|
|
|
|
|||
Дифференцируя ряд (3.2.3) почленно два раза и подставляя в (3.2.1), получим:
∞ |
|
|
|
æ |
A |
∞ |
|
|
ö |
|
|
å- k 2 (A |
cos kt + B |
k |
sin kt) + ç |
0 |
+ å(A |
cos kt + B |
k |
sin kt)÷ω 2 |
= |
||
|
|||||||||||
k=1 |
k |
|
è |
2 |
k |
|
ø |
|
|||
|
|
|
k=1 |
|
|
|
|||||
|
a0 |
∞ |
|
|
|
|
|
|
|
|
|
= |
+ å(ak cos kt + bk sin kt) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
2 |
k=1 |
|
|
|
|
|
|
|
|
|
|
Приравнивая в последней формуле коэффициенты при одинаковых гармониках слева и справа, будем иметь
A ω 2 |
= a |
0 |
, A (ω 2 - k |
2 ) = a |
k |
, B |
k |
(ω 2 - k 2 ) = b |
k |
Þ |
||||||||||||||
0 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
Þ A = |
a0 |
, A = |
|
ak |
, B |
k |
= |
bk |
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
0 |
ω 2 |
|
k |
|
ω |
2 - k 2 |
|
|
|
|
|
ω 2 - k 2 |
|
|
||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
a |
|
|
|
∞ |
a |
|
cos kt + b |
|
|
sin kt |
|
|
||||||||
x(t) = |
|
0 |
|
|
k |
k |
|
|
||||||||||||||||
|
|
|
+ å |
|
|
|
|
|
|
|
|
|
|
|
(3.2.4) |
|||||||||
2ω 2 |
|
|
ω 2 - k 2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|||||||||||||
Из предположения о непрерывности f(t) следует, что ряд (3.2.4) можно почленно дифференцировать. Поэтому ряд (3.2.4) есть реше-
ние уравнения (3.2.1), если только ω 2 ¹ k 2 ни для какого k. Если же число ω целое (ω = k ), то соответствующее слагаемое в правой ча- сти (3.2.4) обращается в ∞, и периодическое решение не существует.
Полученный результат можно было легко предугадать, если
вспомнить, что |
при |
ω = k линейное уравнение &x&+ ω 2 x = |
= a cos kt + b sin kt |
имеет решение вида x(t) = t(Acos kt + B sin kt), не |
|
являющееся периодическим.
Из приведенных рассуждений вытекает следующий вывод: если ω не является целым числом, а f(t) – 2π-периодическая функция, то уравнение (3.2.1) всегда имеет 2π- периодическое решение, доставля- емое формулой (3.2.4). Если же ω = k – целое число, то 2π- периоди- ческое решение уравнения (3.2.1) существует лишь в том случае, ко- гда в разложении функции f(t) в ряд Фурье отсутствуют "резонирую- щие члены" ak и bk, то есть если:
|
|
1 |
2π |
|
1 |
2π |
|
|||
ak |
= |
|
|
ò f (t)cos ktdt = 0, bk |
= |
|
|
ò f (t)sin ktdt = 0. |
(3.2.5) |
|
π |
π |
|||||||||
|
|
0 |
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|||
Если ω = k и выполнено условие (3.2.5), то уравнение (3.2.1) имеет бесконечное число 2π-периодических решений, которые даются фор- мулой:
|
|
|
a |
∞ |
a |
cosmt + b |
sin mt |
|
x(t) = C coskt + C |
2 |
sin kt + |
0 |
+ å |
m |
m |
|
. |
|
|
|||||||
1 |
|
2ω 2 |
m=1 |
|
ω 2 - m2 |
|
|
|
|
|
|
|
|
|
Если же ω ¹ k ("k Î N) , то уравнение (3.2.1) имеет единственное пе-
риодическое решение (3.2.4). |
|
|
|
|
|
||||||||||||||
Пример 3.2.1. Существуют ли периодические решения |
уравне- |
||||||||||||||||||
ния &x&+ 4x = sin 2 t ? |
|
|
|
|
|
|
|
|
|||||||||||
Здесь ω = 2 – целое число. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
2π |
|
|
2 t cos 2tdt = |
|
1 |
2π |
|
|
|||
|
|
a2 |
= |
|
|
|
ò |
sin |
|
|
ò (1 - cos 2t) cos 2tdt |
¹ 0, |
|
||||||
|
|
π |
2π |
|
|||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|||||
|
|
b2 |
= |
1 |
|
2π |
sin 2 t sin 2tdt =0. |
|
|
|
|||||||||
|
|
|
|
|
ò |
|
|
|
|||||||||||
|
|
π |
|
|
|
||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
= 0, b2 |
= 0 не выполняются, |
|
|
||||||
Так как условия a2 |
то периодиче- |
||||||||||||||||||
ского решения у рассматриваемого уравнения нет. |
|
|
|||||||||||||||||
|
|
|
Аналитическая зависимость решений от параметров. |
||||||||||||||||
Рассмотрим задачу Коши для системы уравнений |
|
|
|||||||||||||||||
|
dxi |
|
= f |
i |
(t, x , x |
2 |
,L, x |
n |
, μ), |
|
i =1,2,K, n |
|
|
||||||
|
|
|
|
|
|
||||||||||||||
|
dt |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
(3.2.6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
xi (0) = ai (μ), |
|
|
|
|
|
|
|
|
|
|||||||||
где μ является параметром. |
|
|
|
|
|
||||||||||||||
Теорема 3.2.1. Если в системе (3.2.6) функции fi |
непрерывны по |
||||||||||||||||||
переменной t, а также функции |
|
fi |
и ai аналитические функции пара- |
||||||||||||||||
метра |
|
μ |
|
в |
некоторой |
|
окрестности точки μ = 0, то |
решение |
|||||||||||
x(t) (x(t) Î Rn ) этой системы разлагается в сходящийся при малых μ
ряд по степеням параметра μ: |
|
(t) + L+ μ n x |
|
|
|
|||
x(t, μ) = x |
0 |
(t) + μx |
(t) + μ 2 x |
2 |
n |
(t) + L |
(3.2.7) |
|
|
1 |
|
|
|
|
|||
Доказательство этой теоремы достаточно громоздко и здесь опущено.
Метод разложения решения по степеням малого параметра лежит в основе многих приемов исследования нелинейных колебаний с ма- лой нелинейностью.
Рассмотрим следующую задачу: найти периодическое решение
уравнения: |
|
&x&+ ω 2 x = f (t) + μF(t, x, x&) |
(3.2.8) |
с 2π-периодическими по переменной t |
функциями f(t) и F(t, x, x&) , |
считая, что 2π -периодическое решение |
x0 (t) порождающего уравне- |
ния: |
|
&x&+ ω 2 x = f (t) |
(3.2.9) |
существует и нам известно. Считая, что функция F(t, x, x&) непрерыв-
на по t и является аналитической по переменным x и x&, на основании приведенной выше теоремы, будем искать решение уравнения (3.2.8) в виде ряда (3.2.7) .
Разложим функцию F(t, x, x&) в ряд по степеням (x − x0 ), (x& − x&0 )
в окрестности точки x = x0 , |
x& = x&0 |
|
|
|
|
|
|
||||||||||
F(t, x, x&) = F(t, x0 , x& |
0 ) + |
¶F |
|
|
|
(x - x0 ) + |
|
||||||||||
|
|
|
|||||||||||||||
¶x |
|
x=x0 |
|
||||||||||||||
|
¶F |
|
|
|
|
|
¶2 F |
|
|
x&=x&0 |
|
|
|
|
|
|
|
+ |
|
x=x0 (x& - x&0 ) + |
|
|
|
(x - x0 )2 + |
(3.2.10) |
||||||||||
|
|
|
|
||||||||||||||
¶x& |
|
¶x2 |
x=x0 |
||||||||||||||
|
|
|
x&=x&0 |
|
|
x&=x&0 |
|
|
|
|
|
|
|
||||
+ |
¶2 F |
|
|
(x - x0 )(x& - x& |
0 ) + |
¶2 F |
|
|
|
(x& - x&0 )2 + L |
|
||||||
|
|
|
|
||||||||||||||
¶x¶x& |
|
x=x |
¶ |
2 |
|
x=x |
0 |
|
|||||||||
|
|
|
0 |
|
|
|
|
|
x& |
|
|
|
|
|
|||
|
|
|
|
|
x&=x&0 |
|
|
|
|
|
|
|
|
x&=x&0 |
|
|
|
Подставим в левую и правую части уравнения (3.2.8) вместо &x&, x& и x ряд (3.2.7) и его соответствующие производные, а вместо F(t, x, x&) выражение (3.2.10). Сравнивая коэффициенты при одинаковых сте- пенях μ в левой и правой частях полученного равенства, будем иметь:
ì&x& |
+ω 2x = f (t), |
|
|
|
|
|
|||
ï |
0 |
0 |
|
|
|
|
|
|
|
ï&x& |
+ ω2x = F(t, x , x& ), |
|
|
|
|
||||
ï |
1 |
1 |
0 |
0 |
|
|
|
(3.2.11) |
|
í&&x |
+ω2x |
= ¶F |
x=x0 |
x + |
¶F |
x=x0 |
x& |
||
ï |
2 |
2 |
¶x |
1 |
¶x& |
1 |
|
||
ï |
|
|
|
x&=&x&0 |
|
|
x&=&x&0 |
|
|
|
|
|
|
|
|
|
|||
ï |
|
|
|
|
|
|
|
|
|
îLLLLLLLLLLLLLL |
|
||||||||
Каждое следующее уравнение (3.2.11) будет содержать в правой ча- сти только известные функции, найденные из предыдущих уравне- ний. Поэтому все решения уравнений (3.2.11) могут быть последова- тельно найдены.
Если мы хотим найти 2π-периодическое решение уравнения (3.2.8), то все члены ряда (3.2.7) должны быть 2π-периодическими функциями. Значит каждое из уравнений (3.2.11) должно иметь 2π- периодическое решение. Выясним, когда эти условия выполняются.
1)ω ¹ n , где n – какое-либо целое число. Тогда 2π-периодическое решение у порождающего уравнения (3.2.9) и всех остальных
