
Часть 2 Теория
.pdfуравнений в (3.2.11) существует всегда. Все эти решения могут быть найдены так, как было описано выше.
2)ω = n, n N . Тогда порождающее уравнение (3.2.9) имеет пери- одическое решение лишь при условии равенства нулю коэффи- циентов an и bn в разложении функции f(t) в ряд Фурье, то есть
при выполнении условий:
2π |
2π |
|
ò f (t) cos ntdt = 0, |
ò f (t) sin ntdt = 0. |
(3.2.12) |
0 |
0 |
|
Если условия (3.2.12) выполнены, то порождающее уравнение имеет решение:
x0 (t) = C10 cos nt + C20 sin nt + ϕ0 (t).
Для определения x1(t) имеем второе уравнение из (3.2.11). Оно будет иметь периодическое решение, если
2π |
2π |
|
ò F(t, x0 , x&0 ) cos ntdt = 0, |
ò F(t, x0 , x&0 ) sin ntdt = 0. |
(3.2.13) |
0 |
0 |
|
Уравнения (3.2.13) содержат C10 ,C20 , которые, вообще говоря, определяются из этой системы. Если C10 ,C20 удовлетворяют системе (3.2.13), то все решения второго уравнения в (3.2.11) будут периоди-
ческими с периодом 2π и будут иметь вид: |
|
x1 (t) = C11 cos nt + C21 sin nt + ϕ1 (t) |
(3.2.14) |
При этом C11,C21 опять определяются из двух условий, аналогичных (3.2.12) и (3.2.13), для третьего уравнения из (3.2.11). И так далее.
Как мы видим, в случае 2) (резонансный случай), вообще говоря, не любому 2π-периодическому решению порождающего уравнения соответствует периодическое решение уравнения (3.2.8), задаваемое рядом (3.2.7), которое при μ → 0 сходится к решению порождающе- го уравнения. Существование подобного решение нужно доказать. Такое доказательство составляет содержание известной теоремы Пу- анкаре. Но это доказательство очень громоздко и здесь не приводит- ся.
Пример 3.2.2. Найти приближенно периодическое решение урав- нения:
&x&+ 2x = sin 2t + μ x&2 , где μ – малый параметр.
Решение будем искать в виде ряда по степеням малого параметра,
то есть в виде
x(t) = x0 (t) + μx1 (t) + μ 2 x2 (t) + L .

Тогда
x&(t) = x&0 (t) + μ&x&1 (t) + μ 2 x&2 (t) + L
&x&(t) = &x&0 (t) + μ&x&1 (t) + μ 2 &x&2 (t) + L
Подставим ряды в исходное уравнение
(&x&0 (t) + μ&x&1 (t) + μ 2 &x&2 (t) + L) + 2(x0 (t) + μx1 (t) + μ 2 x2 (t) + L) =
= sin 2t + μ(x&02 + μ 2 x&12 + μ 4 x&22 + 2μx&0 x&1 + 2μ 2 x&0 x&2 + 2μ 3 x&1x&2 + L)
Приравняем коэффициенты при одинаковых степенях параметра μ в левой и правой частях последнего равенства:
μ 0 |
&x& |
+ 2x |
0 |
= sin 2t |
||
μ1 |
0 |
|
|
|
|
|
&x& |
+ 2x = x& |
2 |
(3.2.15) |
|||
μ 2 |
1 |
1 |
|
0 |
||
&x&2 + 2x2 |
= 2x& |
0 x&1 |
||||
KKKKKK
Поскольку ω = 
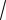 2 , порождающее уравнение имеет единственное пе- риодическое решение, которое будем искать в виде:
2 , порождающее уравнение имеет единственное пе- риодическое решение, которое будем искать в виде:
x0 = Asin 2t + B cos 2t .
После двукратного дифференцирования и подстановки в первое уравнение (3.2.15), получим:
- 4Asin 2t - 4B cos 2t + 2Asin 2t + 2B cos 2t = sin 2t Þ
Þ A = - 12 , B = 0 Þ x0 = - 12 sin 2t.
Для отыскания x1 имеем уравнение
&x&1 + 2x1 = cos2 2t = 12 (1 + cos 4t)
Будем искать x1 в виде:
x1 = M + N cos 4t + Lsin 4t
После двукратного дифференцирования и подстановки в уравнение получим:
-14N cos 4t -14L sin 4t + 2M = 12 + 12 cos 4t Þ N = - 281 , L = 0, M = 14 .
Итак, x1 = 14 - 281 cos 4t .
Подставим найденные функции x0 и x1 в правую часть последнего уравнения (3.2.15). Тогда оно примет вид

&x& |
+ 2x |
2 |
= - |
2 |
cos 2t sin 4t = - |
1 |
sin 3t - |
1 |
sin t. |
(3.2.16) |
|
|
|
||||||||
2 |
|
7 |
7 |
7 |
|
|
||||
|
|
|
|
|
||||||
Будем искать решение последнего уравнения в виде
x2 = Asin 3t + B cos3t + C sin t + D cost .
После двукратного дифференцирования последнего выражения и подстановки в уравнение (3.2.16), находим
A = 491 , B = 0,C = - 17 , D = 0 Þ x2 = 491 sin 3t - 17 sin t.
Итак, справедливо приближенное равенство
x(t) » - 12 sin 2t + μ(14 - 281 cos 4t) + μ 2 (491 sin 3t - 17 sin t). (3.2.17)
Используя пакет Mathcad, сравним полученное решение (3.2.17) с точным решением исходного уравнения на периоде [0, 2π ]. Для этого найдем для решения (3.2.17) значения x(0) и x&(0) , после чего
найдем решение исходного уравнения с заданными начальными условиями, например, методом Рунге-Кутта. Результаты расчетов приведены ниже.
|
Исследуемое уравнение: &x&+ 2x = sin 2t + μ(x&)2 |
|||||||||
|
μ := 0.5 |
|
|
|
|
|
|
|
||
y(t) := |
−1 ×sin(2 ×t) + [μ × (0.25 - 0.035714cos(4 ×t))+ |
|
|
|||||||
|
2 |
|
|
μ 2 × (0.020408sin(3×t) - 0.142857sin(t))] |
||||||
|
|
|
|
|||||||
|
g(t) := |
d |
|
y(t) |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
t := 0,0.01 .. 2 ×π |
|
|
|
|
|
|
|||
|
æ y(0) |
ö |
D(τ , x) := |
é |
x1 |
|
|
ù |
||
|
x := ç |
÷ |
ê |
|
2 |
|
ú |
|||
|
ç |
|
|
÷ |
|
+ μ × (x1) |
+ sin(2 |
|||
|
è g(0) |
ø |
|
ë- 2 × x0 |
|
×τ )û |
||||
|
Z := rkfixed(x,0, 2 ×π ,300, D) |
i := 0..300 |
|
|||||||
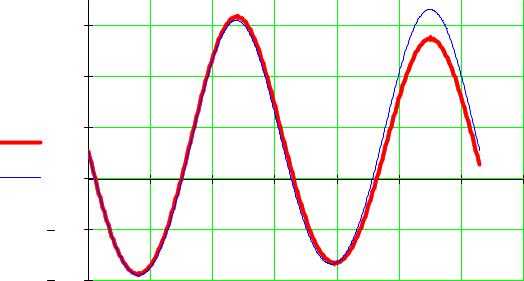
График для μ=0.5 (жирная линия – решение методом Рунге-Кутта) |
|||||||
0.6 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
Z<1> |
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
y(t) |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0.2 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
Z<0> ,t |
|
|
|
|
График для μ=0.25 (жирная линия – решение методом Рунге-Кутта) |
|||||||
|
0.6 |
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
<1> |
0.2 |
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
y(t) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
||||||||
|
0.2 |
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
Z<0> ,t |
|
|
|
|
3.3 Метод Пуанкаре в теории нелинейных колебаний. |
|
|||||||
Автономные уравнения |
|
|
|
|
|
|||
Пусть задано уравнение, правая часть которого не зависит явно
от t:
&x&+ ω 2 x = μF(x, x&) . |
(3.3.1) |
Отсутствие t в правой части приводит к усложнению задачи, так как период искомого решения оказывается неизвестным. Он будет, вооб- ще говоря, зависеть от параметра μ.
Для решения задачи в этом случае нужно преобразовать уравне- ние к новой независимой переменной так, чтобы по новой перемен- ной уравнение уже имело постоянный период, а уже затем искать ре- шение в виде ряда по параметру μ.
Предварительно выполним в (3.3.1) замену времени, положив t1 = ω t . Тогда в новом времени уравнение примет вид:
|
&x&+ x = μF1 (x, x&) , |
(3.3.2) |
||||
где |
производные |
x& и &x& |
вычислены |
по переменной t1, |
а |
|
|
æ |
dx ö |
|
|
|
|
F (x, x&) = Fç x,ω |
|
÷ . |
|
|
|
|
dt |
|
|
|
|||
1 |
ç |
÷ |
|
|
|
|
|
è |
1 |
ø |
|
|
|
|
При μ=0 |
порождающее |
уравнение |
&x&+ x = 0 имеет |
2π- |
|
периодическое решение вида x(t1 ) = C cos(t1 − t0 ), удовлетворяющее
начальным |
условиям x(t0 ) = C, x&(t0 ) = 0 . Периодические |
решения |
|
уравнения |
(3.3.2), если |
они существуют, будут иметь |
период |
2π + α(μ), причем α(μ) |
– аналитическая функция μ и α(μ) → 0 при |
||
μ→ 0 . Пусть:
α(μ) = α1μ + α2 μ 2 + Lα n μ n + L.
Тогда:
2π + α(μ) = 2π (1 + h μ + h |
2 |
μ 2 + Lh |
n |
μ n + L), где h = |
αi |
. |
|
||||||
1 |
|
i |
2π |
|||
|
|
|
|
|
||
Преобразуем уравнение (3.3.2) так, чтобы его решение x(t, μ) имело постоянный период 2π. Этого можно добиться заменой переменных:
t |
1 |
=τ (1 + h μ + h |
2 |
μ 2 |
+ Lh |
n |
μ n + L) |
(3.3.3) |
|
1 |
|
|
|
|
|||
Действительно, если t1 меняется от 0 до 2π + α(μ), то τ |
меняется от |
|||||||
0до 2π.
Вновых переменных уравнение (3.3.2) приобретает вид:
&x&+ (1 + h1μ + h2 μ 2 + Lhn μ n + L)2 x =
= μ(1 + h μ + h |
2 |
μ 2 |
+ Lh |
n |
μ n + L)2 |
× |
(3.3.4) |
1 |
|
|
|
|
|
× F1 (x, (1 + h1μ + h2 μ 2 + Lhn μ n + L)−1 x&),
где все производные вычислены по переменной τ.
Периодическое решение уравнения (3.3.4) будем искать в виде
ряда
x(τ , μ) = x |
0 |
(τ ) + μx (τ ) + L+ μ n x |
n |
(τ ) + L, |
(3.3.5) |
|||
|
|
1 |
|
|
|
|
||
где все xi (τ ) |
– 2π-периодические функции переменной τ. Подставляя |
|||||||
(3.3.5) в уравнение (3.3.4), получим: |
|
|
|
|
|
|||
&x& (τ ) + μ&x& |
(τ ) + μ 2 &x& (τ ) +L+ (1+ h μ + h |
2 |
μ 2 |
+L)2 × |
||||
0 |
1 |
2 |
1 |
|
|
|
||
×(x0 (τ ) + μx1 (τ ) + μ 2 x2 (τ ) +L) =
=(μ + h1μ 2 + h2 μ 3 +L)F1[x, (1+ h1μ + h2 μ 2 +L)−1 ×
×(x&0 (τ ) + μx&1 (τ ) + μ 2 x&2 (τ ) +L)]
Приравнивая коэффициенты при одинаковых степенях параметра μ в левой и правой частях последнего равенства, последовательно полу- чим:
&x&0 + x0 = 0 Þ x0 = C cos(τ - t0 ) |
|
||
&x&1 + x1 = -2h1x0 + F1 |
(x0 , x&0 ) = |
(3.3.6) |
|
= -2h1C cos(τ - t0 ) + |
F1 (C cos(τ - t0 ),-C sin(τ - t0 )) |
||
|
|||
LLLLLLLLLLLLLLL
Для того, чтобы второе уравнение в (3.3.6) имело периодическое ре- шение, необходимо и достаточно, чтобы в его правой части отсут- ствовали резонирующие члены, то есть чтобы выполнялись условия:
2π |
|
|
ò F1[C cos(τ - t0 ),-C sin(τ - t0 )]sin(τ - t0 )dτ = 0 |
(2.10.7) |
|
0 |
|
|
2π |
|
|
ò {-2h1C cos2 (τ - t0 ) + F1[C cos(τ - t0 ),-C sin(τ - t0 )]cos(τ - t0 )}dτ = |
||
0 |
|
|
|
2π |
|
= -2πh1C + |
ò F1[C cos(τ - t0 ),-C sin(τ - t0 )]cos(τ - t0 )dτ = 0 |
|
|
0 |
|
Первое из этих уравнений дает возможность найти С (начальное условие периодического решения), а второе – найти h1. Таким обра-
зом будет приближенно определен период искомого периодического решения:
2π +α(μ) ≈ 2π (1+ h1μ) .
Зная С и h1, можно определить x1 (τ ) и, если это необходимо,
x2 (τ ), x3 (τ ) и так далее.
Пример 3.3.1. Определить решения порождающего уравнения, к которым при μ → 0 приближаются периодические решения уравне-
ния: |
|
&x&+ x = μ x&(9 - x2 ) |
(3.3.8) |
Решения порождающего уравнения имеют вид x(t) = C cos(t − t0 ) .
Для определения искомых значений С воспользуемся первым из уравнений (3.3.7):
2π |
C(9 - C 2 cos2 (t - t0 )) sin 2 (t - t0 )dt = 0 Þ πC(9 - |
C |
2 |
) = 0 Þ |
ò |
|
|||
|
|
|||
0 |
4 |
|
||
Þ C1 = 0,C2,3 = ±6.
При С=0 получаем тривиальное решение x ≡ 0 порождающего уравнения, которое остается решением уравнения (3.3.8) при любом
μ.
При C2,3 = ±6 получаем x = ±6 cos(t − t0 ).
Теорема Ляпунова и несколько практических замечаний
Теорема Ляпунова выделяет класс систем, у которых в некоторой окрестности состояния равновесия существует периодическое реше- ние и дает метод отыскания этого решения.
Теорема 3.3.1. Если уравнение &x&+ ω 2 x = f (x, x&) обладает анали-
тическим первым интегралом |
H (x, x&) = const , причем разложение |
H (x, x&) в окрестности точки x |
= 0, x& = 0 начинается с членов второго |
порядка малости:
H (x, x&) = a11x2 + a12 xx& + a22 x&2 + L,
то все решения уравнения с достаточно малыми начальными услови- ями x(0) = c, x&(0) = 0 есть периодические функции t. Каждое такое
решение является аналитической функцией параметра с. Сформулированная теорема позволяет искать период периодиче-
ского решения уравнения
&x&+ ω 2 x = f (x, x&)
в виде
T= 2π (1+ ch1 + c2h2 + c3h3 +L)
ивводить новое время по формуле
t =τ (1 + ch |
+ c2 h |
2 |
+ c3h + L) , |
(3.3.9) |
1 |
|
3 |
|
|
не вводя малого параметра μ. При этом решение |
x(τ ) следует искать |
|||
в виде ряда |
|
|
|
|
∞ |
|
|
|
|
x(τ ) = åck xk (τ ) |
|
|
(3.3.10) |
|
k=1 |
|
|
|
|
Заметим, что если в уравнении не присутствует явно малый па-
раметр и при этом в окрестности состояния равновесия выполнены условия теоремы Ляпунова, то для поиска периодического решения
можно либо воспользоваться его разложимостью в ряд по начальным отклонениям с (формулой (3.3.10)), либо ввести малый параметр и использовать разложение по степеням малого параметра.
Пример 3.3.2. Найти приближенно периодическое решение урав-
нения Дуффинга |
|
&x&+ x - x3 = 0, x(0) = c, x&(0) = 0. |
(3.3.11) |
Для решения задачи можно ввести малый параметр: x = μ y Þ μ &y& + μ y = μ 3 y3 Þ &y& + y = μ 2 y3 .
Здесь μ считаем малым. Теперь можно воспользоваться рассмотрен- ной выше процедурой отыскания решения уравнения с малым пара- метром.
Заметим, что уравнение Дуффинга обладает аналитическим пер- вым интегралом, для которого выполнены условия теоремы Ляпуно-
ва: H (x, x&) = |
x& |
2 |
+ |
x2 |
- |
x4 |
= C . Поэтому данное уравнение можно |
|
2 |
2 |
4 |
||||||
|
|
|
|
|||||
решать, выполнив замену переменных (3.3.9) и отыскивая решение в виде ряда (3.3.10) по степеням начального возмущения с.
|
Выполним замену (3.3.9). Тогда |
|
|
|
|
|
|||||||||
|
|
|
d 2 x |
= |
d 2 x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
dt 2 |
dτ 2 (1+ ch |
+ c2h +L)2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
||
и уравнение примет вид |
|
|
|
|
|
|
|
|
|||||||
|
d 2 x |
= (x3 - x)(1 + 2ch + 2c2 h |
2 |
+ c2 h2 |
+ c4h2 |
+ 2c3h h |
2 |
+ L) (3.3.12) |
|||||||
|
|
||||||||||||||
|
dτ 2 |
|
1 |
|
1 |
2 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение x(τ ) будем искать в виде ряда (3.3.10). После двукрат-
ного дифференцирования и подстановки этого ряда в уравнение
(3.3.12) будем иметь: |
|
|
|
|
|
|
|
|
|
|
|
|||||
c&x& + c2 &x& |
+ c3 &x& |
+ L= (c3 x3 |
+ 3c2 x2 |
× c2 x |
2 |
+ 3cx × c4 x2 |
+ c6 x3 |
+ L- |
||||||||
1 |
2 |
|
3 |
|
|
1 |
|
1 |
|
1 |
|
2 |
|
2 |
|
|
- cx |
- c2 x |
2 |
- c3 x |
3 |
)[1 + 2ch |
+ c2 (2h |
2 |
+ h2 ) + 2c3h h |
2 |
+ c4 h2 |
]. |
|
||||
1 |
|
|
1 |
|
|
1 |
|
1 |
|
2 |
|
|
||||
Приравнивая коэффициенты при одинаковых степенях с в обеих ча- стях последнего равенства, получим
&x&1 = −x1 |
|
|
|
|
|
|
|
|
||
&x&2 = -x2 - 2x1h1 |
|
|
|
|
|
(3.3.13) |
||||
&x& |
= -x |
|
- x (2h |
|
+ h2 ) + x3 |
- 2h x |
|
|||
3 |
2 |
2 |
|
|
||||||
3 |
|
1 |
1 |
1 |
1 |
|
|
|||
LLLLLLLLLLLLL |
|
|
|
|||||||
Начальные условия для этих уравнений определяются так: |
|
|||||||||
x1 (0) = 1, x&1 (0) = x2 (0) = x&2 (0) = L= 0 |
(3.3.14) |
|||||||||
Первое из уравнений (3.3.13) будет иметь общее решение |
вида |
|||||||||
x1 (τ ) = Acosτ + B sinτ . |
Из |
начальных условий |
находим, |
что |
||||||
A = 1, B = 0. Итак, x1 (τ ) = cosτ . Второе уравнение тогда примет вид
&x&2 + x2 = −2h1 cosτ .
Для того, чтобы это уравнение имело периодическое решение, в его правой части должны отсутствовать резонирующие члены. Это имеет
место лишь при h1 = 0. Таким образом, для x2 получаем уравнение &x&2 + x2 = 0, из которого, с учетом начальных условий (3.3.14), нахо-
дим x2 (τ ) ≡ 0.
Для x3 (τ ) получаем уравнение
&x&3 + x3 = -2h2 cosτ + cos3 τ .
Запишем условия отсутствия резонирующих членов в правой части этого уравнения:
2π
ò (-2h2 cosτ + cos3 τ ) cosτdτ = 0,
0
2π
ò (-2h2 cosτ + cos3 τ ) sinτdτ = 0.
0
Второе из выписанных соотношений всегда выполнено, а первое дает
условие
π (43 - 2h2 ) = 0 Þ h2 = 83.
Итак, x3 (τ ) следует искать из уравнения:
&x&3 + x3 = - 34 cosτ + cos3 τ = - 14 cos 3τ.
Отыскивая 2π-периодическое решение этого уравнения, удовлетво- ряющее начальным условиям x3 (0) = 0, x&3 (0) = 0, получим:
|
|
|
|
|
x3 (τ ) = |
1 |
cosτ - |
1 |
|
cos 3τ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Итак, |
|
|
32 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|||||||||
|
|
|
x(τ ) = c cosτ + c3 ç |
|
|
|
|
cosτ - |
|
|
|
|
|
cos 3τ ÷ |
+ o(c |
4 ). |
|||||||||||||||||||||||||
|
|
|
32 |
32 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
||||||||||
Учитывая (3.3.9), окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
t |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x(t) » c cosç |
|
|
3 |
c |
2 |
|
+ o(c |
3 |
|
÷ |
+ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
ç1+ |
|
|
|
|
|
|
|
) ÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
é |
|
æ |
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
öù |
|
|||
+ c3 |
ê |
1 |
ç |
|
|
|
|
|
t |
|
|
|
|
÷ |
|
|
|
1 |
|
ç |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
÷ú |
+ o(c3 ) |
|||||
ê |
|
cosç |
|
|
|
|
|
|
|
|
|
|
|
÷ |
- |
|
|
|
|
|
cos3ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ú |
||||
32 |
|
|
3 |
|
|
|
|
|
|
|
|
32 |
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||||||||||
|
ê |
ç |
1+ |
c |
2 |
+ o(c |
3 |
÷ |
|
|
|
ç |
|
|
+ |
c |
2 |
+ o(c |
3 |
÷ú |
|
||||||||||||||||||||
|
ê |
|
ç |
|
|
|
|
|
) ÷ |
|
|
|
|
|
|
|
ç |
1 |
|
|
|
|
|
|
|
) ÷ú |
|
||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|||||||||||||||||||||||||
|
ë |
|
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
øû |
|
||||||||||
