
Часть 2 Теория
.pdfПусть q ÎW. Выпустим из этой точки траекторию x(t, q) и пока- |
|
жем, что точка x(τ, q) |
для числа τ любого знака также является |
ω − предельной точкой |
траектории решения x(t, p) . В самом деле, |
если q = lim x(tn , p) , то из группового свойства траекторий динами- |
||||||||
|
n→∞ |
|
|
|
|
x(t, p) следует, |
|
|
ческой |
системы |
и свойства непрерывности |
что |
|||||
x(τ, q) = lim x(tn +τ, p) , а |
это |
и |
означает, |
что |
x(τ, q) |
есть |
||
|
n→∞ |
|
|
|
|
|
|
|
ω − предельная точка траектории x(t, p). |
|
|
|
|||||
Множество A, состоящее из целых траекторий динамической си- |
||||||||
стемы |
(2.6.1), |
называют |
инвариантным |
для |
этой системы: |
|||
x(t, A) A. Если включение |
x(t, A) A справедливо только |
для |
||||||
t ³ 0, то A – положительно инвариантное множество. |
|
|||||||
Заметим, что если решение x(t, p) |
ограничено при t > 0, то мно- |
|||||||
жество его ω − предельных точек не пусто.
Лемма 2.6.1. Если существует дифференцируемая функция v(x), ограниченная снизу (сверху) в положительно инвариантной для си-
стемы (2.6.1) области D Rn , и если производная этой функции в силу системы (2.6.1) знакоотрицательна (знакоположительна) в D,
то все ω − предельные точки траектории любого решения x(t, p) ( p Î D ) лежат на одной и той же поверхности уровня функ-
ции v(x). |
|
p Î D и |
q = lim x(tn , p) . Так как функция |
||
В самом деле, пусть |
|||||
v[x(t, p)] ограничена снизу и не |
n→∞ |
|
|
||
возрастает в D, то существует |
|||||
lim v[x(t, p)] = v∞ . |
В |
силу |
непрерывности |
v(x) |
имеем |
t→+∞ |
|
|
|
|
|
lim v[x(tn , p)] = v(q). Но в силу монотонности функции v[x(t, p)] мо-
n→+∞
жем утверждать, что v(q) = v∞ . Лемма доказана.
2.7 Устойчивость в целом. Теорема Барбашина-Красовского
Предположим, что система (2.6.1) имеет решение x = 0 ( f (0) = 0).
Определение 2.7.1. Решение x = 0 системы (2.6.1) называется устойчивым в целом (или устойчивым при любых начальных возму- щения), если оно устойчиво по Ляпунову и любое решение x(t) си-
стемы обладает свойством | x(t) |→ 0 при t → ∞.
Заметим, что у системы x& = Ax с матрицей A, все собственные значения которой имеют отрицательные вещественные части, реше- ние x = 0 устойчиво в целом.
Определение 2.7.2. Функцию v(x) назовем бесконечно большой, если для произвольного числа N > 0 можно указать такое R > 0 , что v(x) > N при | x |> R .
Поверхности уровня бесконечно большой функции (поверхности {x : v(x) = C = const}) являются ограниченными. В самом деле, для
произвольного C > 0 можно указать R так, что v(x) > C при | x |> R , то есть поверхность уровня целиком лежит в шаре | x |£ R.
Теорема 2.7.1. Если существует дифференцируемая бесконечно большая положительно определенная функция v(x), производная ко- торой v&(x) в силу системы (2.6.1) отрицательно определена при
x Rn , то решение x = 0 системы (2.6.1) асимптотически устой- чиво в целом.
Теорема 2.7.1 допускает обращение и является частным случаем более общей теоремы Барбашина-Красовского.
Теорема 2.7.2 (Теорема Барбашина-Красовского). Если суще-
ствует дифференцируемая бесконечно большая положительно опре- деленная функция v(x) такая, что v&(x) < 0 вне некоторого множе- ства M и v&(x) £ 0 на множестве M, где множество M не содержит
целых траекторий, кроме положения равновесия x = 0, |
то решение |
|||||||||
x = 0 асимптотически устойчиво в целом. |
|
|
|
|
|
|
||||
Доказательство. Пусть |
p Rn – произвольная точка. Выпустим |
|||||||||
из нее |
траекторию |
x(t, p) (t ³ 0) . |
Поскольку |
v&(x) £ 0 , |
то |
|||||
v[x(t, p)] £ v0 = v( p). Так |
как множество |
v(x) £ v0 |
ограничено, |
то |
||||||
x(t, p) – |
ограниченная |
полутраектория |
и |
потому |
она |
имеет |
||||
ω − предельные точки. По лемме 2.6.1 |
все эти точки лежат на одной |
|||||||||
поверхности уровня v = v∞ . |
|
|
|
|
|
|
|
|
||
Если v∞ = 0, то поверхность уровня v = v∞ |
вырождается |
в точку |
||||||||
x = 0 и тогда lim x(t, p) = 0. |
Поскольку из условия v&(x) £ 0 |
следует |
||||||||
|
t→∞ |
|
|
|
|
|
|
|
|
|
устойчивость по Ляпунову решения x = 0, то в этом случае устойчи- вость в целом доказана.
Предположим, что для некоторой точки |
p v∞ ¹ 0. На поверхно- |
||
сти уровня v = v∞ |
лежит ω − предельное |
множество |
траектории |
x(t, p), состоящее |
из целых траекторий. |
Вдоль этих |
траекторий |
v = v∞ = const и, значит, v& = 0. Поэтому W Ì M . По условию теоремы множество M не может содержать целых траекторий, кроме траекто- рии x = 0. Значит v∞ = 0.
Теорема доказана. |
|
|
|
|
Пример 2.7.1. Рассмотрим уравнение |
|
|
|
|
|
&x&+ ϕ(x)x& + f (x) = 0 , |
|
|
(2.7.1) |
в котором f (x),ϕ(x) – непрерывные функции, |
удовлетворяющие |
|||
условиям |
f (0) = 0, ϕ(0) = 0. Найдем условия устойчивости в целом |
|||
решения x = 0. |
|
|
|
|
Выполним замену переменных (замену Льенара) |
|
|||
|
x |
|
|
|
|
y = x& + òϕ(x)dx . |
|
|
|
|
0 |
|
|
|
Тогда получим нелинейную систему |
|
|
|
|
ì |
x |
|
|
|
ïx& = y - òϕ(x)dx, |
|
|
|
|
í |
0 |
|
|
|
ï |
|
|
|
|
îy& = - f (x). |
|
|
|
|
|
x |
|
|
|
Пусть |
v(x, y) = y2 + 2ò f (x)dx . Если |
f (x) × x > 0 при |
x ¹ 0 , то |
|
|
0 |
|
|
|
функция v(x, y) положительно определена. Найдем ее производную в |
||||
силу системы: |
x |
x |
|
|
|
|
|
||
v& = 2yy& |
+ 2 f (x)x& = -2yf (x) + 2 f (x)(y - |
òϕ(x)dx) |
= -2 f (x)ò |
ϕ(x)dx. |
|
|
0 |
0 |
|
|
|
|
|
|
x |
|
|
Анализируя |
v& видим, что |
v& < 0 |
если |
òϕ(x)dx > 0 |
при x > 0 и |
|
|
|
|
|
0 |
|
x |
ϕ(x)dx < 0 при |
x < 0. Эти условия выполнены, если ϕ(x) ³ 0. |
||||
ò |
||||||
0 |
|
|
|
|
|
|
|
Функция v(x, y) будет бесконечно большой если |
x |
||||
|
ò f (x)dx ® ¥ |
|||||
при | x |® ¥. |
|
|
|
|
0 |
|
|
|
|
f (x)x > 0(x ¹ 0) , ϕ(x) ³ 0, |
|||
|
Итак, при |
выполнении |
условий |
|||
x |
f (x)dx ® ¥ при | x |® ¥ решение |
x = 0 |
будет асимптотически |
|||
ò |
||||||
0 |
|
|
|
|
|
|
устойчивым в целом.
Например, для |
уравнения &x&+ x2 x& + x3 |
= 0 все |
перечисленные |
условия выполнены |
и его решение x = 0 |
будет |
асимптотически |
устойчивым в целом. |
|
|
|
Пользуясь полученным результатом, покажем, что при β > 0 си-
стема (2.5.16) устойчива в целом. Это будет означать, что «авторуле- вой» возвращает судно на заданный курс при любых, (а не только при достаточно малых) начальных отклонениях. Так же как это делалось ранее, заменим функцию f (σ ) на непрерывно дифференцируемую
функцию f1 (σ ). После этого перейдем от системы (2.5.16) к уравне-
нию второго порядка относительно σ . Последовательно получим σ&& = &x&1 + β &x&2 = x&2 + β[-x&1 + f1′(σ )(x&1 + β x&2 )] Þ
Þσ&& - β f1¢(σ )σ& = x&2 - β x&1 = -x1 + f1(σ ) - β x2 Þ
Þσ&& - β f1¢(σ )σ& + (σ - f1(σ )) = 0.
Положим |
- |
¢ |
= |
ϕ(σ ),σ |
- |
f1 |
(σ ) |
= ~ |
′ |
|||
|
β f1 (σ ) |
|
|
|
f (σ ). Поскольку |
f1(σ ) ≤ 0 , то |
||||||
|
|
|
|
σ |
~ |
|
|
|
σ 2 |
σ |
|
|
ϕ(σ ) ³ 0. Кроме того ò |
f (σ )dσ = |
2 |
- ò f1 (σ )dσ ® ¥ при σ → ∞ и |
|||||||||
|
|
|
|
0 |
|
|
|
|
0 |
|
||
~ σ σ > σ ¹ . Поэтому σ → 0,σ& → 0 при t → ∞. Иными словами f ( ) 0( 0)
x1 + β x2 ® 0, x2 - β x1 + β f1 (x1 + β x2 ) ® 0 при t → ∞ . Отсюда следу- ет, что x1 ® 0, x2 ® 0 при t → ∞. Значит, при β > 0 x1 = 0, x2 = 0 – устойчивое в целом состояние равновесия.
2.8 Диссипативные системы. Критерии диссипативности
Рассмотрим нелинейную систему:
dx |
= f (t, x), x Î Rn ,t Î (-¥,¥). |
(2.8.1) |
|
dt |
|||
|
|
Будем считать, что для системы (2.8.1) выполнены условия существо- вания и единственности решения x(t,t0 , x0 ) везде в Rtn,x+1 .
Определение 2.8.1. Систему (2.8.1) будем называть диссипа- тивной по Левинсону, если все ее решения бесконечно продолжаемы
вправо и существует число R > 0 такое, что |
|
||
|
|
| x(t,t0 x0 ) |< R . |
(2.8.2) |
|
lim |
||
|
t→∞ |
|
|
Иными словами, для любого решения системы x(t,t0 , x0 ) существует
T (t0 , x0 )такое, что в момент t1 = t0 + T (t0 , x0 ) ³ t0 оно навсегда погру- жается в фиксированный шар {x :| x |≤ R}: | x(t, t0 , x0 ) |< R при t ³ t1
(рис. 2.8.1).
x2 (t0, x0) |
x2 |
x0 |
||||
|
||||||
|
|
|
|
R |
|
R |
|
|
|
|
|||
|
|
|
|
t |
0 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
|
|
||||
Неавтономная система Рис. 2.8.1 |
Автономная система |
|||||
|
|
Два простых критерия диссипативности |
||||
Пусть система (2.8.1) имеет вид |
|
|
||||
|
|
x& = Ax + ϕ(x,t), |
|
(2.8.3) |
||
где A − n × n гурвицева матрица (все собственные значения этой мат- рицы имеют отрицательные вещественные части), а ϕ(t, x)– ограни-
ченная при всех x Rn и t (−∞, ∞) вектор-функция из Rn+1 в Rn .
Вспомним, |
что для произвольных x0 , t0 |
вектор-функция |
x(t) = e A(t−t0 ) x0 |
есть решение линейной системы |
x& = Ax, удовлетво- |
ряющее начальному условию x(t0 ) = x0 . Если матрица A гурвицева,
то, вспоминая структуру этого решения, легко получить оценку
| e A(t−t0 ) x0 |≤ Ce−α (t−t0 ) | x0 |, α > 0,C > 0.
Поскольку приведенная оценка справедлива для произвольного x0 , то
|| e A(t−t0 ) ||≤ Ce−α (t−t0 ) , α > 0,C > 0. |
(2.8.4) |
Теорема 2.8.1. Система (2.8.3) с гурвицевой матрицей А и огра- ниченной функцией ϕ(t, x) диссипативна по Левинсону.
Доказательство. Пусть x(t) = x(t,t0 , x0 ) – произвольное решение системы (2.7.3). Запишем это решение в форме Коши:
t |
|
|
x(t) = e A(t−t0 ) x0 + ò e A(t−s)ϕ[x(s), s]ds . |
(2.8.5) |
|
t0 |
|
|
Пусть для произвольных x и t |
|ϕ(t, x) |< M . Тогда из (2.8.4) и (2.8.5) |
|
получаем: | x(t) |≤ Ce−α (t−t0 ) | x0 |
t |
|
| + ò Ce−α (t−s) Mds. |
|
|
|
t0 |
|
Заметим, что |
|
Ce−α (t−t0 ) | x0 |= 0, а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
t |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t |
|
|
|
|
|
|
|
∞ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M ò Ce−α (t−s) ds £ M ò Ce−α (t−s) ds =MC ò eα (s−t) d(s - t) = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
t0 |
|
|
|
|
|
|
|
t0 |
|
|
t0 |
|
|
|
|
- eα (t0 −t) ] = MC . |
|||||||||||
= lim MC ò eα (s−t) d(s - t) = lim MC [eα (s−t) |
|
t ] = MC lim[e0 |
||||||||||||||||||||||||||
|
t |
|
|
|
|
|
|
|
|
t→∞ |
|
|
|
|
|
t→∞ |
|
|
|
|
|
|
|
|
|
|||
t→∞ |
t0 |
|
|
|
| x(t) |£ |
MC |
α |
|
|
t0 |
α |
|
|
|
|
|
|
|
α |
|
||||||||
|
|
|
|
|
||||||||||||||||||||||||
Итак, |
|
|
, и, следовательно, система (2.8.3) диссипа- |
|||||||||||||||||||||||||
lim |
||||||||||||||||||||||||||||
|
α |
|||||||||||||||||||||||||||
тивна. |
t→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2.8.1. Показать, что система |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x& = y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y& = -ax - by - arctgt sin(xy) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
диссипативна по Левинсону при a > 0,b > 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Матрица |
|
A |
для |
рассматриваемой |
системы |
|
|
имеет вид |
||||||||||||||||||||
æ |
0 |
1 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A = ç |
|
|
|
÷. Ее характеристический полином λ 2+ aλ + b является |
||||||||||||||||||||||||
ç |
- a |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
è |
- bø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
£ π , |
||||||||
полиномом Гурвица при |
a > 0, b > 0. Поскольку |
|
sin(xy) |
|
× |
|
arctg t |
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
то по теореме 2.8.1 система диссипативна. |
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Рассмотрим теперь систему вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x& = Ax + bψ (σ )σ& , |
|
|
|
|
|
|
(2.8.6) |
|
|||||||||||
где ψ (σ )– скалярная функция переменной σ = cT x , b и с – n-
векторы. Такие системы встречаются в теории автоматического регу- лирования и носят название «системы с тахометрической обратной связью».
Выполним в системе (2.8.6) замену Льенара
σ |
σ |
|
y = x - bò |
ψ (τ )dτ = x - bϕ(σ ), ϕ(σ ) =ò |
ψ (τ)dτ. |
0 |
0 |
|
Тогда y& = x& − bψ (σ )σ& = Ax + bψ (σ )σ& − bψ (σ )σ& = Ax. Поэтому |
||
|
y& = Ay + Abϕ(σ ). |
(2.8.7) |
σ
Теорема 2.8.2. Пусть òψ (τ )dτ ограничен при всех σ и матрица
0
A гурвицева. Тогда система (2.8.6) диссипативна.
σ
Доказательство. Из ограниченности функции ϕ(σ ) = òψ (τ)dτ и
0
гурвицевости матрицы A по теореме 2.8.1 следует диссипативность системы (2.8.7). Поскольку x = y + bϕ(σ ), то из ограниченности
функции ϕ(σ ) сразу следует диссипативность системы (2.8.6). Пример 2.8.2. Показать, что при α > 0 все решения уравнения
&x&+ (α + xe−x2 )x& + 3x = 0 ограничены при t → ∞ .
Запишем данное уравнение в виде эквивалентной системы
x& = y, |
|
|
|
|
|
|
|
|
|
|
|
y& = -3x -α y - xe−x2 y. |
|
|
0 |
1 ö |
|
|
|
|
|
||
Эта система |
имеет вид |
(2.8.6), с |
æ |
|
ψ (σ ) = σe−σ |
2 |
, |
||||
A = ç |
|
÷, |
|
||||||||
|
|
|
|
ç |
- 3 |
÷ |
|
|
|
|
|
|
0 |
|
|
è |
- α ø |
|
|
|
|
|
|
æ |
ö |
характеристический полином λ 2 +αλ + 3 |
|||||||||
σ = x, b = ç |
|
÷. При α > 0 |
|||||||||
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
è |
-1ø |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
2 dτ = 0.5, |
|
|
|
||
матрицы |
A |
гурвицев. |
Поскольку |
|
òτ e−τ |
то |
|||||
σ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òτ e−τ 2 dτ < 0.5, "σ . По теореме 2.8.2 |
система диссипативна и, |
зна- |
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
чит, все ее решения ограничены. |
|
|
|
|
|
|
|
|
|||
Одно достаточное условие диссипативности автономных систем
Общая идея формулируемого ниже утверждения следующая: ес- ли условия теоремы Барбашина-Красовского выполнены вне некото- рого шара радиуса R1 , то есть на множестве {x :| x |³ R1}, то система
диссипативна. Рассмотрим систему:
x& = f (x), x Î Rn |
(2.8.8) |
Теорема 2.8.3. Пусть на множестве {x :| x |³ R1} определена не- отрицательная дифференцируемая функция v(x) , обладающая сле- дующими свойствами:
1) lim v(x) = +¥ ,
|x|→∞
2)v&(x) = (grad v(x) × f (x)) £ 0 при | x |³ R1 ,
3)среди решений x(t) системы (2.8.8) не существует таких, для
которых v&[x(t)] º 0 при | x |³ R1 . Тогда система (2.8.8) диссипативна.
Доказательство. Рассмотрим решение x(t, x0 ) (x(0, x0 ) = x0 ) та-
кое, что | x0 |³ R1. В силу условия 2) теоремы v[x(t, x0 )] £ v(x0 )и, сле- довательно, решение x(t, x0 ) при всех t ³ 0 лежит в ограниченном
множестве {x : v(x) £ v(x0 )}. Поэтому рассматриваемое решение про-
должаемо на промежуток [0, ¥) . Положим M = sup v(x) и рассмот-
|x|=R1
рим множество D = {x : v(x) £ M}. В силу условия 1) теоремы, это множество ограничено. Из определения множества D и условия 2) теоремы вытекает, что для произвольного x0 , удовлетворяющего условию | x0 |£ R справедливо включение x(t, x0 ) Ì D при всех t ³ 0.
Покажем теперь, что для произвольного x0 такого, что | x0 |> R1 , найдется t1 > 0, для которого | x(t1 , x0 ) |£ R1. Предположим противное, то есть будем считать, что | x(t, x0 ) |> R1 при "t ³ 0. По доказанному выше решение x(t, x0 ) ограничено и, значит, множество ω -
предельных точек положительной полутраектории этого решения не пусто. Пусть y – какая-либо ω -предельная точка упомянутой по- лутраектории. Тогда | y |³ R1 . Так как функция v[x(t, x0 )] ограничена
снизу |
и |
не |
возрастает, |
то |
существует |
lim v[x(t, x0 )] = |
|
|
|
|
|
|
t→∞ |
= lim v[x(tn , x0 )] = v(y). Через ω -предельную точку y проходит тра-
n→∞
ектория x(t, y), состоящая из ω -предельных точек траектории реше- ния x(t, x0 ) , причем | x(t, y) |³ R1. Эта траектория целиком расположе- на на поверхности уровня v(x) = v(y) = const функции v(x). Поэтому v&[x(t, y)] = 0 . Последнее противоречит условию 3) теоремы.
Итак, для произвольного x0 Rn найдется момент t1 ³ 0 такой, что x(t1 , x0 ) £ R1. Но тогда при всех t ³ t1 x(t, x0 )Î D . Так как мно-
жество D ограничено, то существует |
R > 0 такое, что |
||
|
|
| x(t, x0 ) |< R для произвольного x0 Rn . |
|
|
lim |
|
|
|
t→∞ |
|
|
|
|
Теорема доказана. |
|
|
|
Пример 2.8.3. Рассмотрим систему |
|

ìx& = 2x + y - 1 x3 + 1 x2 ,
ï
í 3 2
ïîy& = -x - y.
Пусть v(x, y) = x2 + y2 . Производная этой функции в силу рас-
сматриваемой системы
v&(x, y) = 2xx& + 2yy& = 2x(2x + y - |
1 |
x3 |
+ |
1 |
x2 ) - 2yx - 2y 2 |
= |
|||
|
2 |
||||||||
|
2 |
|
|
3 |
|
|
. |
||
|
|
|
|
|
|
|
|
||
= - |
x4 |
+ x3 - 2y2 + 4x2 . |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Нетрудно убедиться, что v&(x, y) < 0, если только x2 + y2 достаточно
велико. В самом деле, v& == -2(x2 + y2 ) - |
2 |
x4 + x3 |
+ 6x2 . Существует |
||||||
3 |
|||||||||
|
|
2 |
|
|
|
|
|
||
число γ > 0 такое, что |
- |
x4 + x3 + 6x2 |
£ γ . Пусть x2 |
+ y2 ³ γ . То- |
|||||
|
|||||||||
гда v& ≤ −2γ + γ = −γ < 0. |
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Итак, рассматриваемая система диссипативна. Отметим, что три- |
|||||||||
виальное решение этой |
системы неустойчиво в малом, поскольку |
||||||||
|
|
|
|
æ |
2 |
1 ö |
вещественны |
||
собственные значения матрицы Якоби J (0) = ç |
|
÷ |
|||||||
|
|
|
|
ç |
-1 |
÷ |
|
||
|
|
|
|
è |
-1ø |
|
|||
и имеют разные знаки.
IIIЭлементы теории колебаний
3.1Теория Пуанкаре-Бендиксона
Рассмотрим уравнение &x&+ kx& + bx = 0 , в котором b > 0. Если k > 0, то решение x = 0 асимптотически устойчиво. Если же k < 0, то решение x = 0 полностью неустойчиво в малом.
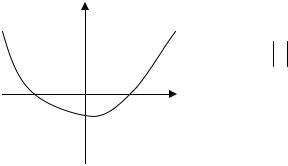
Теперь рассмотрим нелинейное уравне- ние &x&+ ϕ(x)x& + bx = 0, в котором ϕ(x) < 0 при
малых x и ϕ(x) > 0 при больших по абсо- лютной величине значениях x (рис.3.1.1). Яс-
xно, что в рассматриваемом случае может по- явиться решение уравнения, которое ограни- чено и не стремится к нулю при t → +∞. Как
будет вести себя такое решение?
Рассмотрим систему |
|
x& = f (x), x R2 . |
(3.1.1) |
Будем считать, что для этой системы везде в R2 выполнены условия теоремы существования и единственности решения и имеет место не- прерывная зависимость решений от начальных данных. Все эти усло- вия, например, выполнены, если правая часть системы есть диффе- ренцируемая функция везде в R2 .
Пусть x(t) = x(t, x0 ) – ограниченное при t ³ 0 решение системы
(3.1.1) и γ = {x : x = x(t, x0 ),t ³ 0} |
траектория (положительная по- |
лутраектория) этого решения. Так |
как рассматриваемое решение |
ограничено, то множество ω −предельных точек полутраектории γ не пусто. Пусть y −одна из ω −предельных точек.
Теорема 3.1.1. Если y γ , то γ либо точка покоя, либо цикл.
Доказательство. Если у – точка покоя, то по теореме единствен- ности через эту точку проходит единственная траектория, которая совпадает с у. Поскольку y γ , то γ совпадает с у.
