
Часть 2 Теория
.pdf
Доказательство. Справедливость утверждения теоремы сразу вытекает из того факта, что разность любых двух решений системы (2.2.3) есть решение системы (2.2.4).
Условия устойчивости линейных однородных дифференциальных систем.
Теорема 2.2.3. Система (2.2.4) устойчива по Ляпунову тогда и только тогда, когда каждое ее решение x(t) (t0 ≤ t < ∞) ограничено
на [t0 ,∞).
Доказательство. Докажем сначала достаточность утверждения теоремы. Пусть любое решение x(t) системы (2.2.4) ограничено на [t0 ,∞). Рассмотрим фундаментальную матрицу X(t) этой системы,
удовлетворяющую условию X (t0 ) = E . Так как все решения системы
по предположению ограничены, то ограничены и все элементы мат- рицы X(t). То есть существует такое число M > 0 , что || X (t) ||≤ M .
Здесь || X (t) || – норма матрицы X(t), согласованная с нормой вектора |
|||
|
|
|
|
|
n |
2 (t)), то |
|
x(t). Если, например, норма вектора евклидова (| x(t) |= å xi |
|||
|
i=1 |
|
|
|| X (t) ||= 
 ρ , где ρ – максимальное собственное значение симметри- ческой матрицы X (t)X * (t). Любое решение системы (2.2.4) может
ρ , где ρ – максимальное собственное значение симметри- ческой матрицы X (t)X * (t). Любое решение системы (2.2.4) может
быть представлено в виде |
x(t) = X (t) × x(t0 ). Поэтому |
|||
| x(t) |£|| X (t) || × | x(t0 ) |£ M | x(t0 ) |< ε |
если только | x(t0 ) |< |
ε |
= δ . |
|
M |
||||
|
|
|
||
Значит, тривиальное решение, а, следовательно, и любое решение си- стемы (2.2.4) устойчиво.
Доказательство необходимости будем вести от противного. Пусть система (2.2.4) имеет неограниченное решение z(t). Покажем, что в этом случае решение x(t) ≡ 0 неустойчиво. Пусть задано неко-
торое ε > 0. |
|
|||
x(t) = |
z(t) |
|
× |
|
| z(t0 ) | |
||||
|
|
|||
найдется t1 >
Зададимся произвольным δ > 0 и рассмотрим решение
δ |
. Тогда | x(t0 ) |= |
δ |
< δ . В силу неограниченности z(t) |
||||
2 |
|
2 |
z(t1) |
|
|
||
t |
0 |
такое, что x(t ) = |
|
× δ > ε . Значит тривиальное |
|||
|
|||||||
|
1 |
|
| z(t0 ) | |
2 |
|||
|
|
|
|
||||
решение системы (2.2.4) неустойчиво. По теореме 2.2.1 система (2.2.4) вполне неустойчива. Теорема доказана.
Следствие 2.2.3. Если неоднородная система (2.2.3) устойчива, то все ее решения или одновременно ограничены, или не ограничены при t → ∞.
Теорема 2.2.4. Система (2.2.4) асимптотически устойчива то- гда и только тогда, когда все ее решения стремятся к нулю при
t → ∞.
Доказательство. Пусть система (2.2.4) асимптотически устойчи- ва. Тогда все ее решения, включая решение x(t) ≡ 0, асимптотически
устойчивы. |
Поэтому для произвольного решения ς (t) из условия |
|
| ς (t0 ) |< |
(где |
достаточно мало) следует, что lim |ς (t) |= 0 . Пусть |
|
|
t→∞ |
x(t) – произвольное решение системы (2.2.4). Запишем его в виде
x(t) = ς (t) × |
2x(t0 ) |
, |
где ς (t) = |
x(t) |
× |
|
. Поскольку | ς (t0 ) |= |
|
< D , то |
|
|
|
|||||||
D |
|
2 |
2 |
||||||
|
|
|
x(t0 ) |
|
|
||||
lim | ς (t) |= 0 , то есть lim | x(t) |= 0 . |
|
|
|
|
|||||
t→∞ |
|
|
t→∞ |
|
|
|
|
|
|
Пусть все решения системы (2.2.4) стремятся к нулю при t → ∞. Тогда все они, очевидно, ограничены и потому система устойчива по Ляпунову (в силу теоремы 2.2.3). Кроме того, решение x(t) ≡ 0
асимптотически устойчиво. Поэтому, по теореме 2.2.2, система асимптотически устойчива. Теорема доказана.
2.3 Устойчивость линейных систем с постоянными коэффициентами. Критерии Рауса-Гурвица и Льенара-Шипара
Рассмотрим линейную систему |
|
||
|
dy |
= Ay, y Î Rn , |
(2.3.1) |
|
dx |
||
|
|
|
|
где A = (aij ) – постоянная n×n- матрица. Вспомним, что в случае раз- личных вещественных собственных значений λ1,λ2 ,...,λn общее ре-
шение этой системы имеет вид
y = C1e1eλ1x + C2e2eλ2x + ... + Cneneλn x ,
где e1,e2 ,...,en – собственные векторы, соответствующие собствен- ным значениям λ1,λ2 ,...,λn . Ясно, что если Reλi < 0 (i = 1,2,..., n) , то y(x) → 0 при x → +∞ . Следовательно, в этом случае состояние рав-
новесия y = 0 асимптотически устойчиво по Ляпунову. Аналогичная ситуация имеет место и в случае кратных и комплексных собствен- ных значений матрицы A. Справедлива следующая теорема.
Теорема 2.3.1. Линейная однородная система (2.3.1) с постоян-
ными коэффициентами асимптотически устойчива тогда и только тогда, когда все собственные значения матрицы A имеют отрица- тельные вещественные части.
Для того, чтобы пользоваться этой теоремой, нужно уметь нахо- дить собственные значения матрицы A, что является весьма трудоем- кой процедурой в случае n > 2 . Избежать этой процедуры позволяет использование критерия Рауса-Гурвица.
Рассмотрим полином
f (z) = a |
0 |
+ a z + a |
2 |
z2 |
+L+ a |
n |
zn |
(n ³ 1), |
|
|
1 |
|
|
|
|
|
|||
где z – комплексная переменная, а |
ai – действительные или ком- |
||||||||
плексные коэффициенты.
Определение 2.3.1. Полином f(z) называется полиномом Гурви- ца (гурвицевым полиномом), если все его нули имеют отрицательные вещественные части (Re zi < 0) .
Определение 2.3.2. Полином f(z) называется стандартным, ес-
ли a0 > 0, an ¹ 0.
Теорема 2.3.2. Для того, чтобы стандартный полином f(z) с действительными коэффициентами ai был полиномом Гурвица,
необходимо, чтобы выполнялось условие ai |
> 0 |
(i = 1, 2,..., n) . |
|
||||||||||||
Замечание 2.3.1. Легко проверить, |
что для полинома второго |
||||||||||||||
порядка |
f (z) = a |
0 |
+ a z + a |
2 |
z2 условия a |
0 |
> 0, a |
> 0, a |
2 |
> 0 являются |
|||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||
необходимыми и достаточными условиями гурвицевости. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим n×n |
- |
||
æ |
a |
a |
0 |
0 |
|
0 |
L |
0 |
ö |
матрицу |
|
(матрицу |
|||
ç |
1 |
|
|
a1 |
|
a0 |
L |
0 |
÷ |
Гурвица) |
|
|
|
||
ç |
a3 |
a2 |
|
÷ |
|
|
|
||||||||
Г = ç |
M |
|
M |
M |
|
M |
O |
0 |
÷ |
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
÷ |
(здесь принято, |
что |
|||
ç |
|
a2n−2 a2n−3 |
|
a2n−4 L an |
÷ |
||||||||||
èa2n−1 |
|
ø |
as = 0 при s < 0 и s > n ). |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Например, для полинома пятой степени
f (z) = a0 + a1z + a2 z2 + a3 z3 + a4 z4 + a5 z5
матрица Г выглядит так:
æ a |
a |
0 |
0 |
0 |
0 |
ö |
||||
ç |
|
1 |
|
a1 a0 |
0 |
÷ |
||||
ça3 a2 |
÷ |
|||||||||
G = ça |
5 |
a |
4 |
a |
3 |
a |
2 |
a |
÷ |
|
ç |
|
|
|
|
1 |
÷ |
||||
ç 0 |
0 |
a5 |
a4 |
a3 |
÷ |
|||||
ç |
0 |
0 |
0 |
0 |
|
÷ |
||||
è |
a5 ø |
|||||||||
Теорема 2.3.3 (теорема Гурвица). Для того, чтобы стандарт- ный полином f(z) был полиномом Гурвица, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Γ были положи- тельными:
D |
1 |
= a |
> 0, D |
2 |
= |
a1 |
|
a0 |
> 0,L, D = a |
n |
D |
n−1 |
> 0. |
|
(2.3.2) |
|||||
|
1 |
|
|
|
a3 |
|
a2 |
|
|
|
|
|
|
|
|
|
||||
Легко проверить (сделать это самостоятельно), что для полинома |
||||||||||||||||||||
третьей степени |
|
f (z) = z3 + b z2 |
+ b |
z + b |
|
условия (2.3.2) |
приобре- |
|||||||||||||
тают вид: |
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b1 > 0,b2 > 0,b3 > 0, b1b2 > b3, |
f (z) = z4 + b z3 |
+ b z2 |
|
|
||||||||||||||||
а для полинома четвертой степени |
+ b z + b |
|||||||||||||||||||
эти условия такие: |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
b > 0,b > 0,b b > b ,b (b b - b ) > b2b . |
|
|
|
|
||||||||||||||||
1 |
|
4 |
1 |
2 |
|
3 |
3 |
1 |
2 |
3 |
|
|
1 |
4 |
|
|
|
|
||
Иногда |
вместо |
теоремы Гурвица удобнее пользоваться равно- |
||||||||||||||||||
сильным ему критерием Льенара-Шипара.
Теорема 2.3.4. Для того, чтобы полином f(z) с действительными коэффициентами был полиномом Гурвица, необходимо и достаточ- но, чтобы все его коэффициенты были положительны (ai > 0) и вы-
полнялись условия n−1 > 0, n−3 > 0, n−5 > 0,..., где k те же, что и в формулах (2.3.2).
Пример 2.3.1. Определить область асимптотической устойчиво-
сти линейной системы
ìx& = -x + ay
ïíy& = bx - y + az , где a, b – действительные параметры.
ïîz& = by - z
Решение. Характеристическое уравнение системы имеет вид
- λ -1 |
a |
0 |
|
= 0 Þ (λ +1)[λ2 + 2λ + (1- 2ab)] = 0. |
|
||||
b |
- λ -1 |
a |
|
|
0 |
b |
- λ -1 |
|
|
Один из корней характеристического уравнения λ1 = −1. Два других
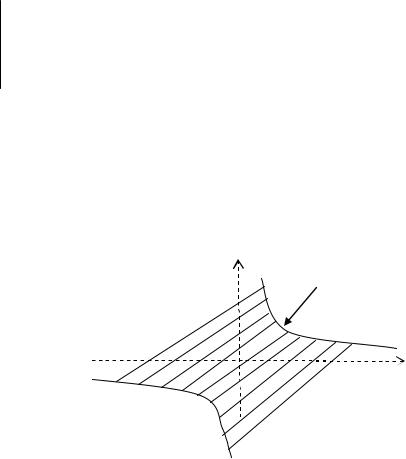
корня, согласно замечанию 2.3.1, будут иметь отрицательные веще- ственные части, если выполняются условие 1− 2ab > 0. Область устойчивости рассматриваемой системы на плоскости (a,b) изобра- жена на рис.2.1.3.
b |
b = |
1 |
|
|
2a |
||||
|
|
|||
|
|
|
|
|
a
Рис. 2.1.3
Пример 2.3.2. При каких a и b полином λ4 + 2λ3 + aλ2 + 3λ + b является полиномом Гурвица?
Решение. Составим для данного полинома матрицу Гурвица и применим критерий Льенара-Шипара.
æ |
3 |
b |
0 |
0 |
ö |
|
|
|
||
ç |
2 |
a |
3 |
b |
÷ |
|
|
|
||
ç |
÷ |
Þ a > 0,b > 0, D1 |
= 3 |
> 0, |
||||||
G = ç |
0 |
1 |
2 |
a |
÷ |
|||||
ç |
÷ |
|
|
|
||||||
ç |
0 |
0 |
0 |
1 |
÷ |
|
|
|
||
è |
ø |
|
|
|
||||||
|
|
|
3 |
b |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
D3 = |
|
2 a 3 |
> 0 Þ 6a - 4b - 9 > 0. |
|
||||||
|
|
|
0 |
1 |
2 |
|
|
|
|
|
Окончательно получаем условия: b > 0; 6a > 4b + 9.
2.4 Функция Ляпунова. Теоремы Ляпунова об устойчивости. Теорема Четаева
Пусть V(x) – функция переменной x Î Rn . Будем говорить, что функция V(x) положительно определена в окрестности U точки x = a ,
если V (x) > 0 при |
x ÎU (x ¹ a) |
и V (a) = 0. Если же в окрестности U |
|||||||
выполнены условия V (x) < 0 при |
x ¹ a и V (a) = 0, то будем гово- |
||||||||
рить, что функция V(x) отрицательно определена |
в окрестности U. |
||||||||
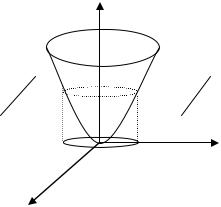
Например, функция V (x) = x2 + x2 |
+L+ x2 положительно определе- |
||||||||
|
|
|
1 |
|
2 |
n |
|
|
|
на в любой окрестности точки |
x = 0. Отметим, что при n = 2 урав- |
||||||||
|
|
|
|
|
|
|
нение V (x) = x2 + x2 опреде- |
||
|
|
|
V |
|
|
1 |
2 |
||
|
|
|
|
ляет параболоид вращения. |
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Линии уровня V = C этой |
||
|
|
|
V=C |
|
|||||
|
|
|
|
поверхности |
представляют |
||||
|
|
|
|
|
|
|
собой окружности, которые |
||
|
|
|
|
|
|
|
|||
|
|
|
|
x2 |
|
стягиваются |
в точку (0,0) при |
||
|
|
|
|
|
C → 0 (рис. 2.1.4). |
|
|||
|
|
|
|
|
|
|
|
||
|
|
x1 |
Рис. 2.1.4 |
|
Аналогичным |
свойством |
|||
|
|
|
обладают поверхности уровня |
||||||
любой положительно определенной функции.
Лемма 2.4.1. Если функция V(x) положительно определена в не- которой окрестности U точки x = a , то при достаточно малом C > 0 множество {x :V (x) = C} представляет собой замкнутую по- верхность, стягивающуюся при C → 0 к точке x = a .
Пример 2.4.1. Пусть V (x) = xT Hx, где H положительно опреде- ленная матрица. Тогда V(x) – положительно определенная функция (положительно определенная квадратичная форма). Поверхности уровня такой функции xT Hx = C представляют собой эллипсоиды, стягивающиеся к точке x = 0 при C ® 0.
Определение 2.4.1 Положительно определенная в некоторой окрестности U точки x = a дифференцируемая в этой окрестности
функция V(x) называется функцией Ляпунова для системы |
|
x& = f (x), x Rn , |
(2.4.1) |
если ее производная V&(x) = (gradV (x), f (x)) не положительна в ука-
занной окрестности.
Приведенная ниже теорема А.М.Ляпунова является одной из центральных теорем так называемого второго метода Ляпунова, иг-
рающего важную роль в качественной теории дифференциальных уравнений.
Теорема 2.4.1. Если в некоторой окрестности U положения рав- новесия x = a системы (2.4.1) существует функция Ляпунова V(x), то это положение равновесия устойчиво по Ляпунову.
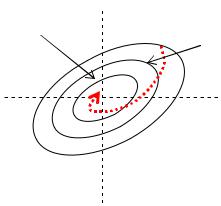
Доказательство. Прежде чем непосредственно перейти к доказа- тельству, наметим его геометрическую идею для случая n = 2 . Пусть, для простоты a – точка (0,0). Как было отмечено выше, линии уровня V (x) = C – замкнутые (при малых С) кривые, охватывающие начало координат. Эти кривые стягиваются в точку (0,0) при C → 0 и кривая
V (x) = C1 лежит внутри кривой V (x) = C2 при C1 < C2 (рис. 2.1.5) |
|
|||||||||
|
|
|
Выпустим |
фазовую |
траекто- |
|||||
|
V = C2 |
|
||||||||
|
V=C1 |
рию γ |
в момент времени t = 0 |
из |
||||||
|
|
точки |
x0 |
(V (x0 ) = C0 > C1 > C2 ). |
||||||
|
|
|
||||||||
|
|
|
Поскольку |
|
V&(x) ≤ 0, |
|
|
то |
||
|
|
V = C0 |
V[x(t)] ≤ V (x0) = C0 |
при t ³ 0 . |
По- |
|||||
|
|
этому |
точка |
на |
траектории |
γ |
не |
|||
|
|
|
может сильно отклониться от по- |
|||||||
|
|
Рис. 2.1.5 |
ложения равновесия. При |
C0 → 0 |
||||||
точку (0,0) (рис. 2.1.5). |
линия |
V (x0 ) = C0 |
стягивается |
в |
||||||
|
|
|
|
|
|
|
|
|||
x2 |
Перейдем теперь к строгим рассуж- |
|||||||
дениям. |
Пусть |
a = 0 . |
Выберем |
ε > 0 |
||||
|
|
|
столь |
малым, |
чтобы |
|
шар |
|
|
|
|
Kε = {x :| x |£ ε} лежал в окрестности U |
|||||
|
|
|
точки x = 0 (рис. 2.1.6). Пусть Sε |
грани- |
||||
Kδ |
Sε |
|
||||||
|
ца шара – сфера | x |= ε . Так как Sε – за- |
|||||||
|
x1 |
|||||||
|
|
мкнутое ограниченное множество, а V(x) |
||||||
U |
– непрерывная функция и |
V (x) > 0 на |
||||||
Sε , то minV (x) = k > 0. |
|
|
|
|||||
|
|
|
|
|
|
|||
Рис. 2.1.6 |
x Sε |
|
Kδ |
= {x :| x |£ δ}, |
||||
Рассмотрим |
шар |
|||||||
содержащийся в U. Так как V (0) = 0, то δ > 0 можно выбрать столь |
||||||||
малым, чтобы выполнялось неравенство V (x) < k при x Î Kδ . |
Пока- |
|||||||
жем, что если | x0 |< δ , то | x(t, x0 ) |£ ε |
при 0 £ t < ¥. |
Тем самым тео- |
||||||
рема будет доказана. |
|
|
|
|
|
|
||
Так как V&(x) ≤ 0 в U и V (x0 ) < k , то V (x) < k при 0 £ t < ¥ вдоль траектории x(t, x0 ). Следовательно, траектория, которая начинается
в шаре Kδ , не может пересечь сферу Sε , так как на Sε V (x) ³ k и V (x) < k вдоль рассматриваемой траектории. Теорема доказана.
Теорема 2.4.2. (Теорема Ляпунова об асимптотической устойчи-
вости). Пусть в некоторой окрестности U положения равновесия x = 0 системы (2.4.1) существует функция Ляпунова V(x) такая, что ее производная V&(x) в силу этой системы отрицательно определена в U. Тогда положение равновесия x = 0 асимптотически устойчиво.
Доказательство. Выберем шары Kδ и Kε также, как это было сделано при доказательстве теоремы 2.4.1. Если | x0 |< δ , то
| x(t, x0 ) |£ ε при 0 £ t < ¥. Рассмотрим функцию w(t) = V[x(t, x0 )].Так как V&[x(t, x0 )] ≤ 0, то функция w(t) не возрастает и, следовательно,
существует lim w(t) = A ³ 0 .
t→+∞
Если A = 0, то lim x(t, x0 ) = 0 , поскольку V (x) > 0 при x ¹ 0 и |
|
t→+∞ |
|
V (0) = 0. В этом случае теорема доказана. |
|
Допустим, что A > 0 и приведем это предположение к противо- |
|
речию. В рассматриваемом случае w(t) ³ A при всех t ³ 0 |
и суще- |
ствует α Î (0,ε) такое, что выполнено | x(t, x0 ) |³ α при |
0 £ t £ ¥. |
Действительно, если бы это было не так, то на рассматриваемой тра- ектории имелись бы точки сколь угодно близкие к точке x = 0 и функция V(x) в этих точках принимала бы сколь угодно малые значе- ния. В шаровом слое α ≤| x |≤ ε функция V&(x) по условиям теоремы
строго отрицательна. В силу непрерывности функции V&(x) в указан- ном шаровом слое (и, значит, на рассматриваемой траектории) вы- полнено соотношение V&(x) £ -m < 0 . Поэтому w&(t) = V&[(x(t, x0 )] £ -m. Интегрируя последнее неравенство, получим
w(t) ≤ w(0) − mt < 0 при t > wm(0) .
Пришли к противоречию с предположением w(t) ³ A > 0 при t ³ 0. Теорема доказана.
Теорема 2.4.2 не дает оценки скорости стремления | x(t, x0 ) | к нулю при t → +∞. Следующее утверждение позволяет получить та-
кую оценку. |
|
|
|
Теорема 2.4.3. |
Пусть x = 0 |
положение равновесия системы |
|
(2.4.1) и существует положительно определенная в |
некоторой |
||
окрестности точки |
x = 0 функция V(x) такая, что |
|
|
V&(x) £ -αV (x), |
V (x) ³ M | x |β , |
(2.4.2) |
|
где α, β , M – некоторые положительные числа.
Тогда существует такая постоянная C > 0, что
−αt
| x(t, x0 ) |£ Ce β при t ³ 0
для всех достаточно малых | x0 |.
Доказательство. Пусть w(t) = V[x(t, x0 )]. Тогда
dtd [eαt w(t)]= eαt [αw(t) + w&(t)] £ 0.
Интегрируя последнее неравенство, получим
eαt w(t) - w(0) £ 0 Þ w(t) £ e−αt w(0) Þ V[x(t, x0 )] £ e−αtV (x0 ).
По условию (2.4.2):
M | x(t, x0 ) |β £ V[x(t, x0 )] £ e−αtV (x0 ) Þ| x(t, x0 ) |£ β V (x0 )e −βαt
M
при t ³ 0. Теорема доказана.
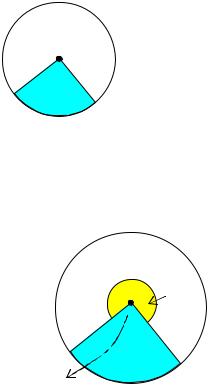
Пусть U = {x :| x |£ h} некоторый шар, содержащий положение равновесия x = 0 системы (2.4.1), U1 – открытая область, имеющая 0 своей граничной точкой (рис.2.1.7), а V(x) – непрерывно дифферен-
цируемая в U функция. |
|
|
|
Теорема |
2.4.4 (Теорема Четаева). Пусть |
0 U |
V (x) > 0, V&(x) > 0 при x ÎU1 и для любого α > 0 |
|
U1 |
существует |
β = β (α) > 0 такое, что из условия |
V (x) ³ α следует, что V&(x) > β для любого x ÎU1. |
||
Рис. 2.1.7 |
Пусть V (x) = 0 в тех граничных точках области |
|
U1, которые лежат в U. Тогда положение равно- |
||
|
весия x = 0 неустойчиво по Ляпунову при t → +∞. |
|
U U1δ
U1
x(t, x0 )
Рис. 2.1.8
Доказательство. Пусть δ > 0 – любое сколь угодно малое число. Обозначим че-
рез U1δ шар радиуса δ с центром в точке
x = 0 и покажем, что любая траектория
γ = {x : x = x(t, x0 ), x0 ÎU1δ IU1 ,t ³ 0} с
ростом t пересечет ту часть границы об- ласти U1, на которой V (x) ¹ 0 (рис.2.1.8).
Это и будет означать неустойчивость по Ляпунову состояния равновесия x = 0.
Из условия |
x0 ÎU1δ IU1 следует, |
что V (x0 ) > 0. |
Но тогда |
|
V[x(t, x0 )] ³ V (x0 ) |
при t ³ 0 до тех пор, |
пока x(t, x0 ) ÎU1. Положим |
||
α = V (x0 ). Тогда |
для |
тех t, для которых x(t, x0 ) ÎU1, |
выполнено |
|
V&[x(t, x0 )] ³ β (α) > 0. |
Интегрируя последнее неравенство, получим |
|||
|
V[x(t, x0 )] ³ V (x0 ) + βt . |
(2.4.3) |
||
Из последнего соотношения вытекает существование такого t1 > 0, что x(t1, x0 ) Î ¶U1 (находится на границе области U1). В самом деле, если бы имело место включение γ Ì U1 при всех t ³ 0, то из нера- венства (2.4.3) следовала бы неограниченность функции V(x) в обла- сти U1, а это противоречит предположению о непрерывности функ- ции V(x) в шаре U. Итак, существует t1 такое, что x(t1, x0 ) Î ¶U1 и при этом V[x(t, x0 )] ³ α > 0.
