
Часть 2 Теория
.pdfПример 3.3.2. |
Найти |
приближенно периодическое |
|
решение |
||
уравнения: |
|
|
|
|
|
|
&x&+ x = μ(4 - x2 )x& |
|
|
|
μ n + L) . |
||
Выполним замену времени t =τ (1 + h μ + h |
2 |
μ 2 + Lh |
n |
|||
|
|
1 |
|
|
||
Тогда в новом времени исходное уравнение примет вид |
|
|
||||
&x&+ (1+ h μ + h μ 2 |
+Lh μ n +L)2 x = |
|
|
|
|
|
1 |
2 |
n |
|
|
|
(3.3.15) |
= μ(1+ h μ + h μ 2 |
+Lh μ n +L)2 (4 - x2 )x& |
|
||||
|
|
|||||
1 |
2 |
n |
|
|
|
|
Решение уравнения (3.3.15) будем искать в виде ряда (3.3.5). При
этом будем искать решение с начальными условиями x(0) = c, x&(0) = 0.Тогда:
x0 (0) = c, x&0 (0) = x&1 (0) = x&2 (0) = L= 0.
Здесь x0 (τ ) – решение порождающего уравнения, то есть уравне-
ния (3.3.15) при μ = 0. Поэтому x0 (τ ) = c cosτ.
Сравнивая коэффициенты при μ1 в обеих частях равенства
(3.3.15), найдем |
|
|
|
|
|
|||
&x& |
|
+ x = (4 - x2 )x& |
0 |
- 2h x |
0 |
|
||
1 |
|
1 |
|
1 |
|
|||
Учитывая вид x0 (τ ), получим |
|
|
|
|||||
&x& |
+ x |
= -(4 - c2 cos2 |
τ )c sinτ - 2h c cosτ |
(3.3.16) |
||||
1 |
|
1 |
|
|
|
|
1 |
|
Найдем условия существования периодического решения у урав- нения (3.3.16). Для этого запишем соотношения (3.3.7). Чтобы запи- сать это соотношение, нужно последовательно умножить правую часть уравнения (3.3.16) на sinτ и cosτ и, проинтегрировав получен- ные выражения, приравнять интегралы в нулю. В данном случае (убедиться в этом самостоятельно) результатом реализации описан- ных операций будут соотношения:
æ |
|
1 |
c2 |
ö |
|
|
cç4 |
- |
|
÷ |
= 0, h |
= 0. |
|
|
||||||
è |
|
4 |
|
ø |
1 |
|
|
|
|
|
Таким образом, c = 0 или с = ±4 . Для c = 0 получаем тривиальное решение порождающего уравнения, которое остается решением ис- следуемого уравнения при любом μ. Для c = 4 получаем периодиче- ское решение порождающего уравнения x0 (τ ) = 4 cosτ. Тогда для
определения x1 (τ ) будем иметь уравнение
|
+ x = -(4 -16 cos2 |
æ |
|
1 + cos 2τ ö |
||
&&x |
τ )4sinτ = -16ç1 |
- 4 |
|
|
÷sinτ = |
|
|
|
|||||
1 |
1 |
è |
|
2 |
ø |
|
|
|
|
||||
=16(sinτ + 2 cos 2τ sinτ ) =16sin 3τ. |
|
|
|
|
||
Итак, для x1 (τ ) получаем уравнение |
|
|
|
|
||
&x&1 + x1 =16sin 3τ. |
|
|
|
|
(3.3.7) |
|
Общее решение последнего уравнения имеет вид:
x1 (τ ) = C1 cosτ + C2 sinτ + Asin 3τ + B cos3τ .
Дважды дифференцируя это выражение и подставляя в (3.3.17), найдем значения А и В:
A = -2, B = 0 Þ x1 (τ ) = C1 cosτ + C2 sinτ - 2sin 3τ.
Используя начальное условие x&1 (0) = 0 , находим C2 = 6.
Итак, |
x1 (τ ) = C1 cosτ + 6sinτ - 2sin 3τ. Теперь, приравнивая коэф- |
||||||||||||||||
фициенты при μ 2 |
|
слева и справа в |
(3.3.15), найдем (учитывая, что |
||||||||||||||
h1 = 0): |
|
|
|
|
|
|
|
|
|
|
+ (4 - x2 )x& |
|
|
|
|
|
|
|
&x& + x |
2 |
= -2h |
2 |
x |
0 |
- 2x |
0 |
x x& |
0 |
. |
|
|||||
|
2 |
|
|
|
|
|
|
0 |
|
1 |
|
|
|||||
Подставляя найденные выше значения x0 (τ ) и x1(τ ) , получим |
|
||||||||||||||||
&x& |
+ x |
2 |
= -8h |
2 |
cosτ -16sinτ + 64sinτ cos |
2 τ + 32C sinτ cos2 |
τ + |
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
+ 256 cosτ - 512 cos3 τ + 256 cos5 τ = F(τ ).
Запишем условия существования периодического решения для по-
следнего уравнения
2π |
F(τ ) cosτdτ = -8h2 |
+ 32π = 0, |
|
|
|
ò |
Þ C1 |
= 0, |
|||
0 |
|
|
|||
2π |
F(τ ) sinτdτ = 8C1π = 0 |
h2 = 4. |
|||
ò |
|||||
|
|
||||
0 |
|
|
|
|
|
Теперь окончательно можем записать x1 (τ ) = 6sinτ - 2 sin 3τ , h2 = 4. Выпишем, наконец, приближенное решение исходного уравнения
æ |
|
|
|
|
t |
|
ö |
|
|
x(t) » 4 cosç |
|
|
|
|
|
|
÷ |
+ |
|
|
|
|
2 |
|
2 |
|
|||
ç |
1 |
+ 4μ |
+ o(μ |
÷ |
|
||||
è |
|
|
) ø |
|
|||||
é |
æ |
|
t |
ö |
æ |
|
t |
öù |
+ o(μ 2 ). |
+ μ ê6 sinç |
|
÷ |
- 2 sin 3ç |
|
÷ú |
||||
1 + 4μ 2 |
|
1 + 4μ 2 |
|
||||||
ê |
ç |
+ o(μ 2 ) ÷ |
ç |
+ o(μ 2 ) ÷ú |
|
||||
ë |
è |
|
|
ø |
è |
|
|
øû |
|
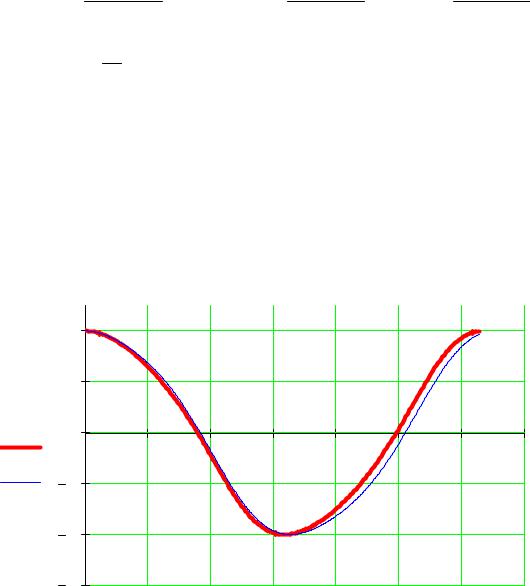
Используя пакет Mathcad, сравним полученное решение |
с решением |
|||||||||||||
исходного уравнения методом Рунге-Кутта на периоде [0, 2π]. |
|
|||||||||||||
Исследуемое уравнение: &x&+ x = μ(4 - x2 )x& |
|
|||||||||||||
μ := 0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
t |
|
ö |
æ |
æ |
t |
|
|
ö |
|
æ |
3×t |
öö |
|
y(t) := 4 × cosç |
|
|
2 |
÷ + μ × |
ç6 |
×sinç |
|
|
2 |
÷ - 2 ×sinç |
|
÷÷ |
||
ç |
+ 4 |
× μ |
÷ |
ç |
ç |
|
× μ |
÷ |
|
ç |
+ 4 × μ |
2 ÷÷ |
||
è1 |
|
ø |
è |
è1+ 4 |
|
ø |
|
è1 |
øø |
|||||
g(t) := |
d |
y(t) |
t := 0,0.01 .. 2 ×π |
|
|
|
|
|
|
|
||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
æ y(0) |
ö |
|
|
D(τ , x) := |
é |
|
|
x1 |
2 |
|
|
ù |
||
x := ç |
|
÷ |
|
|
ê |
× x0 + μ × (x1) |
|
|
ú |
|||||
èg(0) |
ø |
|
|
|
|
ë- 2 |
|
+ sin(2 ×τ )û |
||||||
Z := rkfixed(x,0, 2 ×π ,300, D) |
|
|
i := 0..300 |
|
|
|||||||||
График для μ=0.1 (жирная линия – решение методом Рунге-Кутта) |
||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z<1> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
2 |
|
3 |
|
4 |
|
5 |
|
6 |
7 |
||
y(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z<0> ,t |
|
|
|
|
|
|
||
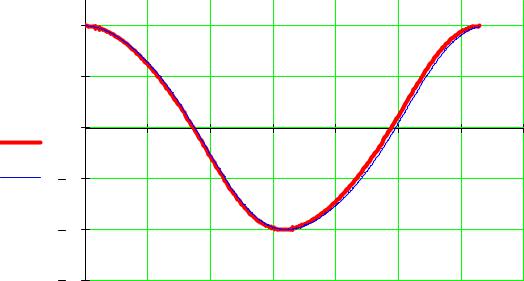
График для μ=0.07 (жирная линия – решение методом Рунге-Кутта) |
||||||||||||||
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Z<1> |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
y(t) |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
Z<0> ,t |
|
|
|
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК |
|
|
|
||||
1.Бибиков Ю.Н. Общий курс обыкновенных дифференциальных уравнений. Издательство Ленинградского университета. Л.1981. – 232 с..
2.Боровских А.В., Смагина Т.И.,Тананика А.А., Федотенко Г.Ф. Задания для самостоятельной работы студентов по дифференциальным уравнениям. Ча- сти 1 и 2. Издательство Воронежского университета. 1991. – 40 с.
3.Болгов В.А., Демидович Б.П., Ефименко В.А. и др. Сборник задач по мате- матике для втузов. Специальные разделы математического анализа. М. "Наука". 1981. – 368 с.
4.Демидович Б.П. Лекции по математической теории устойчивости. М. "Наука". 1967. – 472 с.
5.Краснов М.Л., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновен- ным дифференциальным уравнениям. М. "Высшая школа". 1978. –285 с.
6.Кузнецов Л.А. Сборник заданий по высшей математике. (типовые расчеты). М. "Высшая школа". 1983. 176 с.
7.Леонов Г.А., Буркин И.М., Шепелявый А.И. Частотные методы в теории не- линейных колебаний. Часть 1. Изд.-во Санкт-Петербургского университета. 1992. – 366 с.
8.Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Изд.-во "Вышэйшая школа". Минск 1974. – 766 с.
9.Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М. "Наука". 1970. –279 с.
10.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М. "Наука". 1970. – 331 с.
11.Проскуряков А.П. Метод Пуанкаре в теории нелинейных колебаний. М. "Наука". 1977. – 256с.
12.Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные урав- нения. Примеры и задачи. М. "Высшая школа". 1989.– 383 с.
13.Тихонов А.Н., Васильева А.Б., Свешников.А.Г. Дифференциальные уравне-
ния. М. "Наука". 1980. – 230 с.
14.Федорюк М.В. Обыкновенные дифференциальные уравнения. М. "Наука". 1980. – 350 с.
15.Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М. "Ин-
теграл-пресс". 1998. – 207 с.
16.Хартман Ф. Обыкновенные дифференциальные уравнения. М. "Мир". 1970. –720 с.
17.Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление.
М. "Наука". 1969. – 326 с.
