3.3.2. Нелинейная парная регрессия

Если между результативным и факторным признаком существует нелинейная зависимость, то она выражается с помощью соответствующих нелинейных функций.

Для описания нелинейной связи между ииспользуют следующие виды функций:

1) параболическая ;

2) кубическая парабола ;

4) гиперболическая ;

5) логарифмическая ;

6) степенная ;

7) показательная ;

8) экспоненциальная ;

9) логистическая

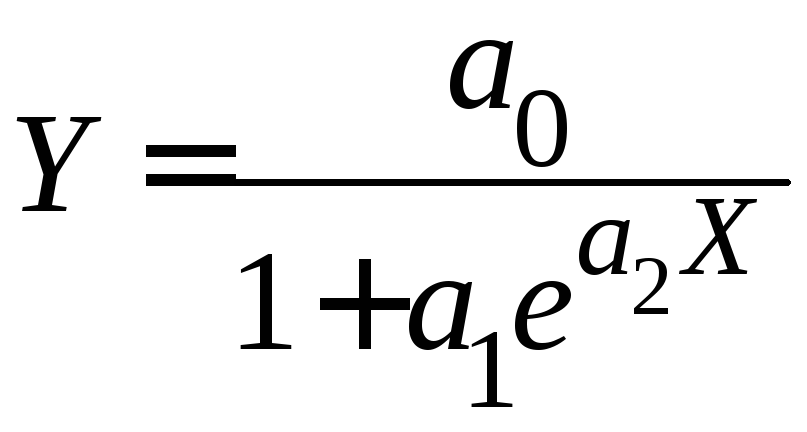
и некоторые другие.

Здесь – неизвестные параметры (коэффициенты регрессии), подлежащие определению. Необходимо подобрать значения этих параметров, обеспечивающие наилучшее приближение теоретической функцией эмпирических данных.

Различают 2 класса нелинейных регрессионных моделей:

1) регрессии, нелинейные относительно переменных, но линейные по параметрам (полиномы разных степеней, гипербола и др.);

2) регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная и др.).

Если коэффициенты регрессии входят в регрессионную модель линейно, то метод наименьших квадратов приводит к системе линейных алгебраических уравнений относительно искомых коэффициентов. В противном случае – к нелинейной системе уравнений.

Так в случае выбора теоретической функции в виде полинома k–й степени (функция линейна относительно параметров), исходя из критерия метода наименьших квадратов

(вычисляя и приравнивая нулю частные производные ,), получим линейную систему уравнений

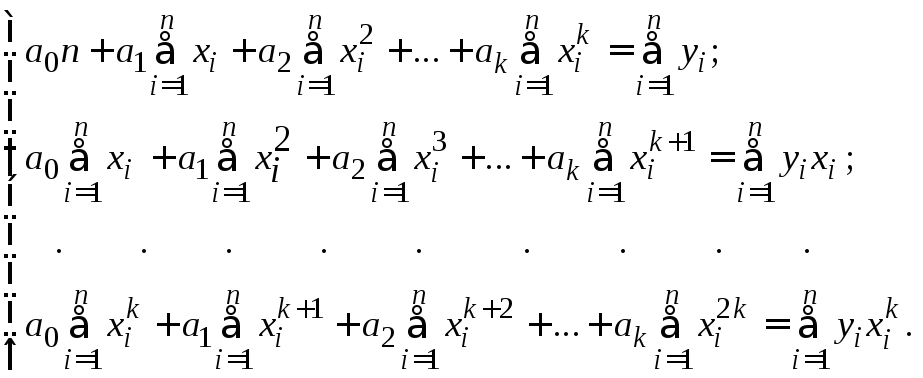
Решая эту систему, найдем неизвестные параметры .

В случае параболической регрессионной модели коэффициенты регрессии определяются из системы линейных уравнений

Если в качестве теоретической функции выбрана гиперболическая функция, то параметры регрессии определяются из линейной системы

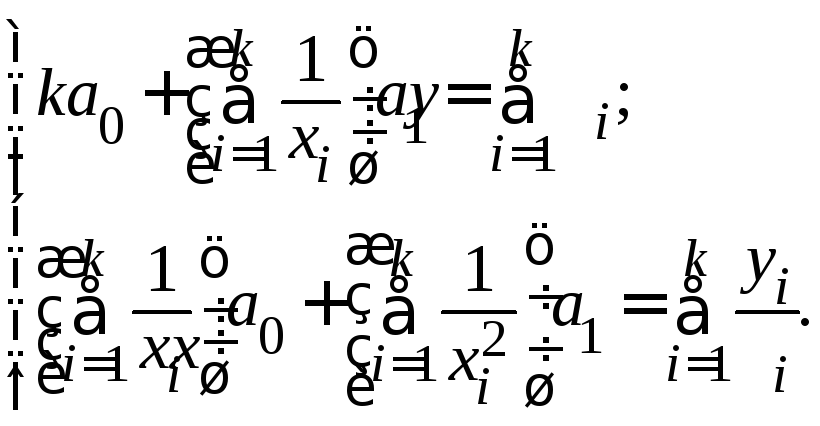
Если модель нелинейна относительно параметров регрессии, то она в ряде случаев с помощью соответствующих преобразований может быть приведена к линейному виду.

Если же модель не может быть приведена к линейному виду, то для оценки параметров в этом случае приходиться решать системы нелинейных уравнений, используя итерационные методы. В этом случае успех в нахождении параметров регрессии зависит от сложности полученной системы.

3.3.3. Множественная регрессия

Построение функциональной связи между результирующим показателем и двумя и более факторами носит название множественной (многофакторной, многомерной) регрессии. При этом уравнение регрессии имеет вид

.

В случае множественной регрессии выбор формы связи оказывается значительно более сложным по сравнению с парной регрессией.

Практика построения многофакторных моделей показывает, что реально существующие в экономике зависимости можно описать, используя следующие типы моделей:

1) линейная ;

2) степенная ;

3) экспоненциальная ;

4) параболическая ;

5) гиперболическая .

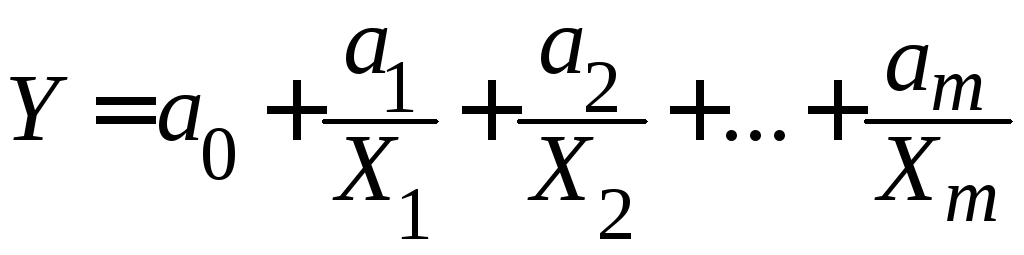Основное значение имеют линейные модели (относительно параметров регрессии) в силу своей простоты. Нелинейные формы зависимости часто преобразуются к линейным путем линеаризации.

Наиболее приемлемым способом определения вида уравнения регрессии является метод перебора различных уравнений регрессии.

Наилучшие значения параметров регрессии определяются методом наименьших квадратов.

Коэффициенты регрессии находятся по критерию:

,

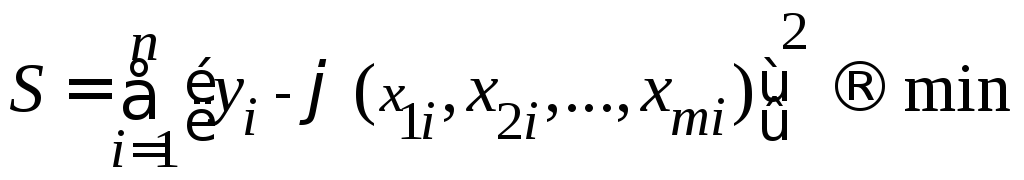где – значение результативного фактора (зависимой переменной) в–ом наблюдении;– значения факторов в–ом наблюдении;– количество наблюдений.

Реализация этого критерия приводит к системе уравнений

,

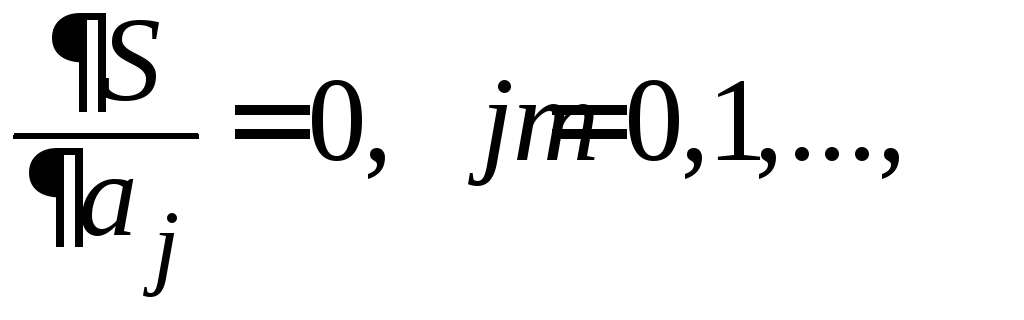из которой определяются .

Построение линейной модели множественной регрессии

Линейная модель множественной регрессии имеет вид:

.

Это уравнение содержит неизвестные параметры .

Эти коэффициенты регрессии есть случайные величины, так как их значения оцениваются на основе выборочных наблюдений. Поэтому полученные расчетные параметры не являются истинными, а представляют собой лишь их статистические оценки.

Модель линейной регрессии, в которой вместо истинных значений параметров присутствуют их оценки (а именно такие модели регрессии и применяются на практике), в матричном виде запишем следующим образом:

,

где – вектор–столбец зависимой переменной (матрица размером ),представляющий собой наблюдаемых значений ();

– матрица наблюдаемых значений независимых переменных , размер которой (добавлен единичный столбец для определения);

– подлежащий оцениванию вектор–столбец неизвестных параметров (матрица размером );

– вектор–столбец случайных отклонений (матрица размером ).

Таким образом, имеем :

.

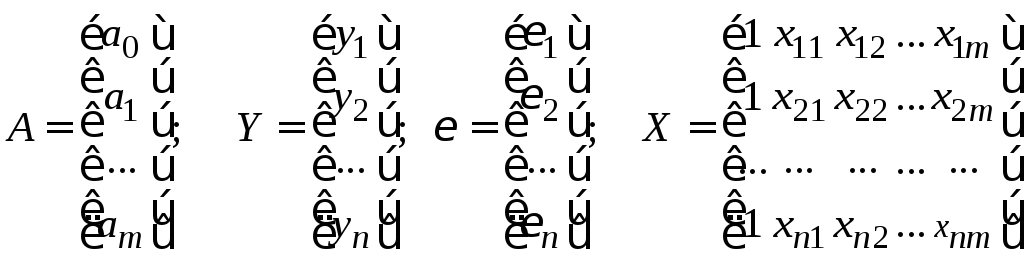Для регрессионной модели, линейной относительно коэффициентов регрессии (или приведенной к указанному виду), коэффициенты регрессии удобно находить методом наименьших квадратов.

После определения коэффициентов регрессии можно рассчитать разности фактических и теоретических значений результативного признака в каждом наблюдении

Для рассматриваемой линейной модели

.

Величина называется остатком в–ом наблюдении. Эти остатки можно считать выборочными значениями неизвестного остатка, являющегося случайной величиной.

Следует заметить, что если при построении регрессионной модели будем добавлять новые наблюдения, то величины могут изменяться, так как при этом, вообще говоря, будут изменяться коэффициенты регрессии и, следовательно, теоретические значения результативного признака. Поэтому регрессионный анализ включает не только построение самой регрессионной модели, но и исследование остатков. При этом сами остаткиследует рассматривать как случайные величины.

Каждый коэффициент регрессии является случайной величиной, свойства которой зависят от свойств остаточного члена в регрессионной модели.

Для того чтобы регрессионный анализ, основанный на методе наименьших квадратов, давал наилучшие результаты, а использование критериев Стьюдента и Фишера при проверке статистической достоверности коэффициентов регрессии и уравнения регрессии было обосновано, необходимо выполнение некоторых предположений относительно поведения остатков .

Для регрессионных моделей, линейных относительно объясняющих переменных , случайный член должен удовлетворять четырем условиям Гаусса–Маркова:

1. Остаток в каждом–ом наблюдении имеет нулевое математическое ожидание, то есть

для любого ;

2. Дисперсия остатков одинакова для всех наблюдений, то есть

для любого ;

3. Остатки в разных наблюдениях не зависят друг от друга, то есть ковариация

при ;

4. Остаток и каждая объясняющая переменная в любом наблюдении не зависят друг от друга, то есть

для любого ,

где − значение объясняющей переменнойв–ом наблюдении.

Ковариация определяется формулой

Наряду с условиями Гаусса–Маркова предполагается нормальность распределения остатков. Если остатки нормально распределены, то нормально будут распределены и коэффициенты регрессии.

Предположение о нормальном распределении остатков основывается на центральной предельной теореме, согласно которой, если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, то приближенно она будет иметь нормальное распределение, даже если отдельные случайные составляющие не имеют нормального распределения.

Случайный член определяется рядом факторов, которые явно не входят в уравнение регрессии. Поэтому даже если ничего не известно о распределении этих факторов или об их сущности, можно предположить, что случайный член регрессионной модели распределен по нормальному закону.

Отметим, что если уравнение регрессии включает постоянный член , то обычно предполагают, что первое условие Гаусса–Маркова выполняется автоматически, так как роль постоянного члена состоит в определении систематической тенденции в результативном признаке, которую не учитывают объясняющие переменные , включенные в регрессионную модель.

Используя формулу и учитывая, что из первого условия имеем, можем записать второе условие Гаусса–Маркова в виде

для любого .

Второе условие известно как гомоскедастичность, что означает «одинаковый разброс».

Третье условие предполагает отсутствие систематической связи между остатками в любых двух наблюдениях.

Учитывая, что по первому условию и, получаем

.

Поэтому третье условие можно записать в виде

при .

Аналогично четвертое условие Гаусса–Маркова может быть записано следующим образом:

для любого .

Если выполнены условия Гаусса–Маркова, то метод наименьших квадратов дает несмещенные, эффективные и состоятельные оценки коэффициентов регрессии _.

Возвращаясь к линейной регрессионной модели, записанной в матричном виде, необходимо отметить, что столбцы матрицы должны быть линейно независимыми, а число наблюденийдолжно превосходит ранг матрицы(ее максимальный ранг – ()).

Линейная модель, для которой выполняются условия 1 – 4 и остатки нормально распределены, называется классической нормальной моделью множественной регрессии.

Если не выполняется только условие нормального распределения остатков, то модель называют классической линейной моделью множественной регрессии.

С использованием имеющихся исходных статистических данных критерий метода наименьших квадратов выглядит следующим образом:

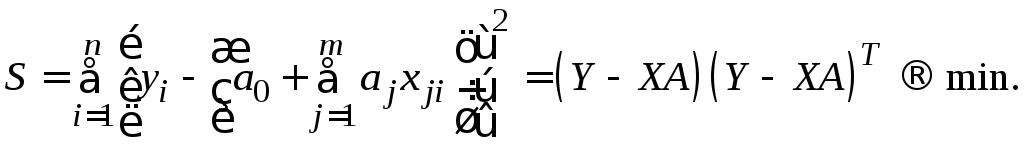
Здесь Т – символ транспонирования матрицы.

В матричном виде решение множественного регрессионного анализа определяется соотношением:

.

Для конкретного –го наблюдения имеем соотношение

Коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак , если переменную увеличить на одну единицу своего измерения при неизменном значении других факторов, закрепленных на среднем уровне (то есть является нормативным коэффициентом и имеет размерность отношения размерностей и ).

Обычно предполагается, что случайная величина имеет нормальный закон распределения с математическим ожиданием равным нулю и некоторой дисперсией.

Одним из условий построения регрессионной модели является предположение о линейной независимости объясняющих переменных, то есть столбцы и строки матрицы исходных данных должны быть линейно независимы. Для экономических показателей это условие выполняется не всегда.

Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости уравнений в системе алгебраических уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели.

Мультиколлинеарность может возникать в силу разных причин. Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания.

В частности, так может случиться, когда значения одной независимой переменной являются лагированными значениями другой.

Явление мультиколлинеарности в исходных данных считают установленным, если коэффициент парной корреляции между двумя переменными больше 0,8.

Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.

В качестве критерия отсутствия мультиколлинеарности может быть принято соблюдение следующих неравенств:

Если приведенные неравенства (или хотя бы одно из них) не выполняются, то в модель включают тот фактор, который наиболее тесно связан с .

Анализ статистической значимости параметров модели

Значимость отдельных коэффициентов регрессии проверяется по Т–критерию путем проверки гипотезы о равенстве нулю j–го параметра уравнения (кроме свободного члена):

, ,

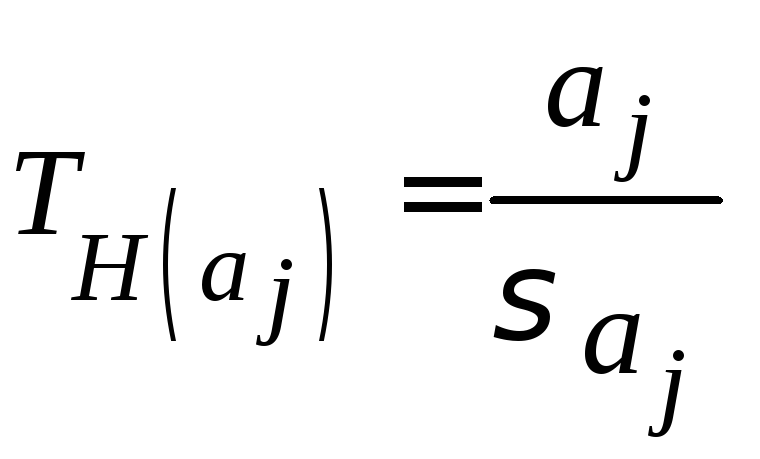где – стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии .

Величина представляет собой квадратный корень из произведения несмещенной оценки точности модели и j–го диагонального элемента матрицы :

.

Здесь – диагональный элемент матрицы .

В матричном виде имеем соотношение:

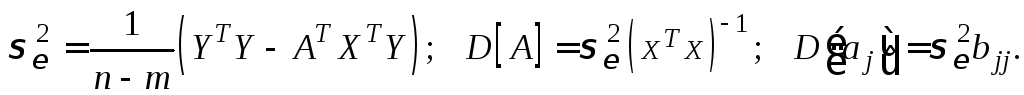
Табличное значение критерия определяется при (n–2) степенях свободы и соответствующем уровне значимости  ( = 0.1; 0.05; 0.01).

Если расчетное значение критерия превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым.

В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).

Доверительный интервал для коэффициентов регрессии имеет вид:

Проверка значимости и качества модели регрессии

Значимость уравнения регрессии в целом сводится к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при независимых переменных:

Для проверки значимости модели регрессии используется F–критерий Фишера:

,

где п – число наблюдений; m – число независимых переменных, включенных в модель.

Если расчетное значение больше табличного (критического) значения при заданном уровне значимости , то модель считается значимой (адекватной имеющимся наблюдениям).

Для оценки качества модели множественной регрессии часто вычисляют коэффициент множественной корреляции (индекс корреляции) R и коэффициент детерминации R² .

В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных.

Скорректированный (нормированный) коэффициент детерминации рассчитывается по соотношению:

,

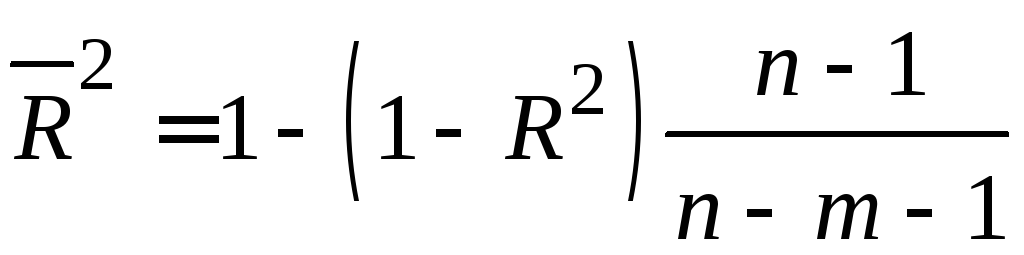где п – число наблюдений; m – число независимых переменных.

В целом качество модели оценивается стандартным для математических моделей образом: по адекватности и точности на основе анализа остатков регрессии

Расчетные значения результирующего показателя получаются путем подстановки в модель фактических значений всех включенных факторов.

Оценка влияния отдельных факторов на зависимую переменную

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из–за различия единиц измерения и разной степени колеблемости.

Для устранения таких различий при интерпретации модели применяются средние частные коэффициенты эластичности и бета–коэффициенты (стандартизованные коэффициенты регрессии) , которые рассчитываются соответственно по формулам:

,

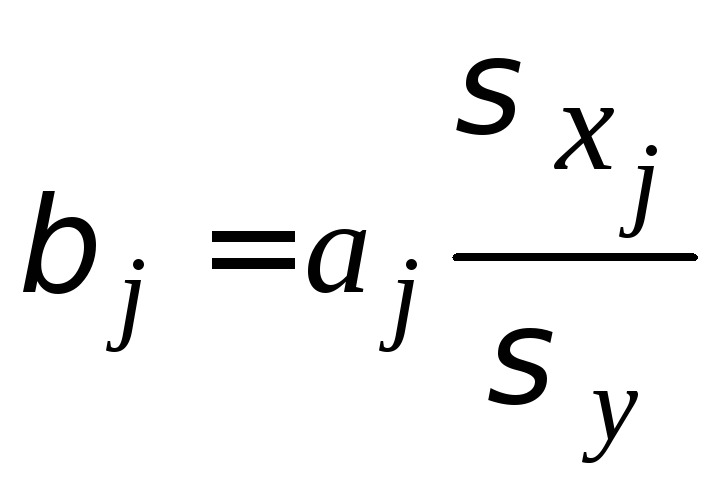где – среднеквадратическое отклонение фактора .

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент ( не учитывает степень колеблемости факторов).

Бета–коэффициент показывает, на какую часть величины среднего квадратического отклонения изменится зависимая переменная с изменением соответствующей независимой переменной на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

Уравнение регрессии в стандартизованной форме имеет вид:

Здесь – стандартизованные переменные

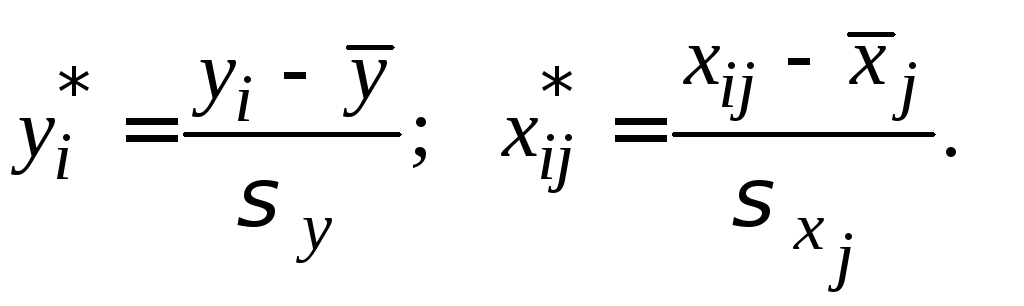
В результате такого нормирования средние значения всех стандартизованных переменных равны нулю, а дисперсии равны единице.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта–коэффициентов:

,

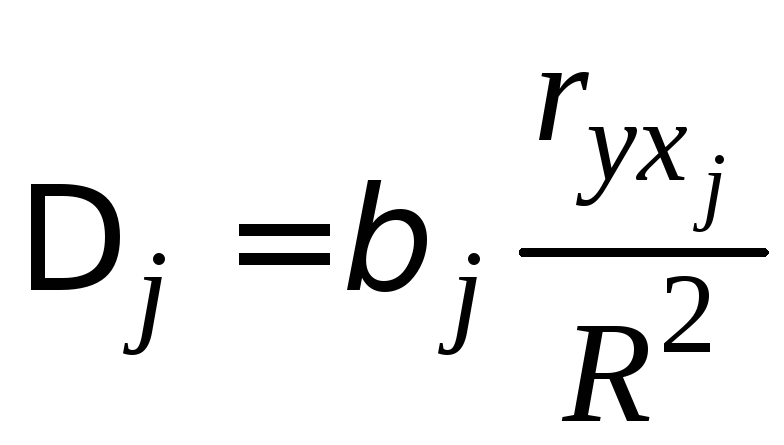где – коэффициент парной корреляции между фактором и зависимой переменной ; – коэффициент детерминации.

Использование многофакторных моделей для анализа и прогнозирования развития экономических систем

Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Данные могут не иметь временной структуры, но и в этих случаях вполне может возникнуть задача оценки значения зависимой переменной для некоторого набора независимых (объясняющих) переменных, которых нет в исходных наблюдениях. Прогнозирование в эконометрике – это построение оценки зависимой переменной.

При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.

Для прогнозирования зависимой переменной на τ шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов

Их оценки могут быть получены на основе временных экстраполяционных моделей или заданы пользователем (экспертом). Эти оценки подставляются в модель и получаются прогнозные оценки.

Для того чтобы определить область возможных значений результативного показателя при рассчитанных значениях факторов следует учитывать два возможных источника ошибок:

1) рассеивание наблюдений относительно линии регрессии;

2) ошибки, обусловленные математическим аппаратом построения самой линии регрессии.

Ошибки первого рода измеряются с помощью характеристик точности, в частности, величиной .

Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными (часто нормально распределенными) величинами.

Для линейной модели множественной регрессии доверительный интервал рассчитывается следующим образом:

.

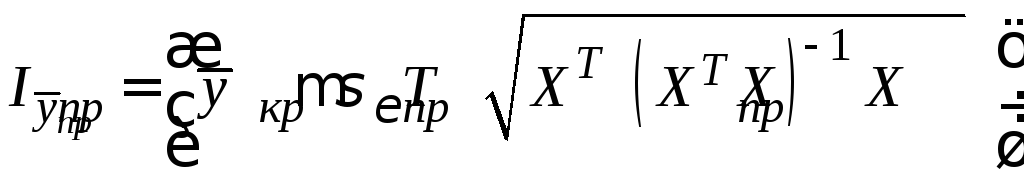Здесь

.