5.2. Уравнение Бернулли для установившегося движения несжимаемой жидкости

Рассмотрим одно из основных уравнений гидродинамики – уравнение Бернулли, которое представляет собой математическое выражение закона сохранения энергии. Это уравнение широко применяется при проведении инженерных расчетов. для случая слабодеформированного потока это уравнение обычно дополняется уравнением неразрывности (4.4)

Для получения уравнения Бернулли рассмотрим энергетические преобразования, происходящие в элементарной струйке (рис. 5.2).

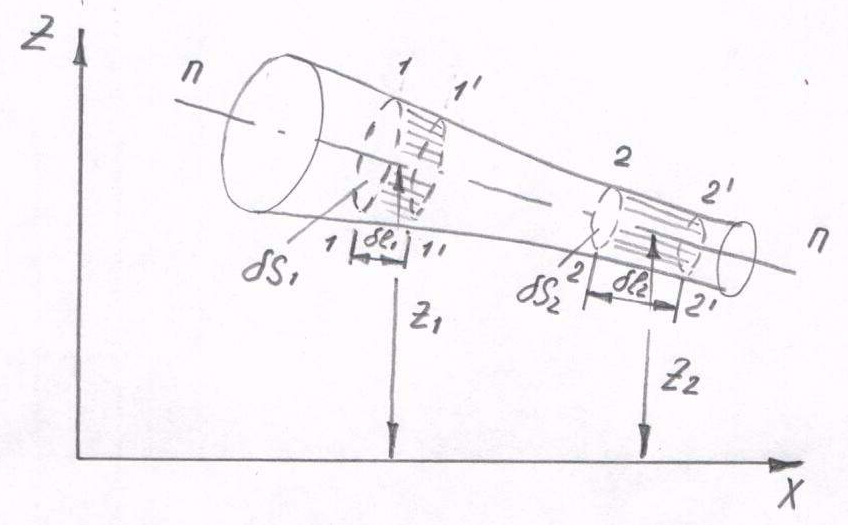
Рис. 5.2. К выводу уравнения Бернулли

В струйке, определяемой осью n-n проведем сечения 1 и 2. За время t сечение 1 переместится на l₁ в положение 1', а сечение 2 – на l₂ в положение 2'. При этом по условию неразрывности (4.3)

; ;

–элементарный объем жидкости.

Объем 1-2 за время t в результате движения жидкости перемещается в положение 1-2'. Так как движение потока считаем установившимся, то в его части, выделенной сечениями 1' и 2, изменения параметров не происходит. Поэтому все изменения, в том числе и энергии, произошедшие в результате перемещения объема 1-2 в положение 1'-2' происходят вследствие перемещения объема W из положения 1-1' в положение 2-2'.

Из-за малых поперечных размеров элементарной струйки можно считать, что все частицы объема 1-1' движутся со скоростью V₁ , а объема 2-2' - со скоростью V₂.

Тогда изменение кинетической энергии массы жидкости при перемещении из положения 1-1' в положение 2-2' будет

(5.4)

В соответствии с теоремой о кинетической энергии изменение кинетической энергии движущейся массы равно полной работе сил, действующих на эту массу.

Вычислим работу сил, действующих на рассматриваемую массу.

– работа силы тяжести равна произведению веса на понижение его центра тяжести, т.е.;

– работа сил давления:

работа сил давления, приложенных к боковой поверхности элементарного объема, равна 0, т.к. эти силы перпендикулярны направлению перемещения частиц жидкости.

работа сил давления, приложенных к основаниям сжатых объемов 1-1' и 2-2' определяется разностью:

;

– работа сил сопротивления.

Эта работа возникает при любом режиме движения вязкой жидкости. Она определяется касательными напряжениями и вихревыми движениями. Так как силы сопротивления действуют против направления движения, то их работа, отнесенная к единице веса протекающей жидкости равна .– затраты удельной энергии на преодоление сопротивлений между рассматриваемыми сечениями.

В результате, учитывая равенство (5.4) по теореме о кинетической энергии будем иметь:

или

;

перенося слагаемые, относящиеся к первому сечению в левую часть, а ко второму в правую, перепишем последнее уравнение в виде

;

обозначая удельный вес , окончательно получим

; (5.5)

Уравнение (5.5) – это уравнение Бернулли для установившегося движения элементарной струйки вязкой несжимаемой жидкости.

Уравнение Бернулли было получено в 1738 г. и имеет чрезвычайно важное значение в гидравлике. Даниил Бернулли (1700 – 1782 г.г) – выдающийся математик и физик, один из членов известного семейства Бернулли, в числе которых видные математики и физики. Д. Бернулли по происхождению швейцарец, член Петербургской академии наук, жил в Петербурге с 1725 по 1733 г, где написал свой знаменитый труд «Гидродинамика»; занимался многими вопросами механики жидкостей и газов.

В целом ряде гидравлических задач главное значение имеют нормальные напряжения (давления) в жидкости, а касательными напряжениями и связанными с ними сопротивлениями движению можно пренебречь, т.е. принять = = 0. Тогда для этого частного случая установившегося движения струйки несжимаемой идеальной (невязкой) жидкости уравнение (5.5) запишется в виде:

(5.6)

В левой и правой частях уравнения (5.6) записана полная механическая энергии единицы объема жидкости.

В случае покоящейся жидкости из уравнения (5.6) легко получается основное уравнение гидростатики (3.8): .

Определим гидравлический смысл всех трех слагаемых, входящих в уравнение Бернулли.

Слагаемое z измеряет высоту расположения движущейся частицы жидкости над горизонтальной плоскостью и имеет размерность длины. Координату z можно назвать отметкой движущейся частицы над горизонтальной плоскостью.

Слагаемое может быть представлено высотой такого столба жидкости, который в данной точке линии тока произвел бы давление, равное действительно существующему здесь давлению p.

Слагаемое . Как известно из теоретической механики, выражение дает значение той высоты, с которой должно свободно упасть тело, чтобы, падая в пустоте, в конце пути приобрести скорость V. Поэтому слагаемое может быть названо высотой, соответствующей скорости V или, как это принято в гидравлике, скоростным напором.

Уравнение (5.6) может быть переписано в давлениях . Здесьp – статическое давление; – скоростное или динамическое давление;– весовое давление.

Рассмотрим геометрический смысл уравнения Бернулли.

Возьмем элементарную струйку с осью a-b (рис. 5.3).

Рис. 5.3. К рассмотрению геометрического смысла уравнения Бернулли

Пусть точки a и b этой оси лежат соответственно в сечениях 1-1 и 2-2 и имеют отметки z₁ и z₂ над некоторой плоскостью сравнения yox. Отложим от точки a по вертикали отрезок aa', равный пьезометрической высоте , а затем от точки a' – отрезок a'a'', равный скоростному напору. Такое же построение выполним для точки b в сечении 2-2 и для любого числа других сечений струйки. Т.к. по уравнению (5.6) сумма трех слагаемых: z,,вдоль всей струйки постоянна, то, следовательно, вершины полученных вертикальных отрезков a'', b'' и т.д. должны находиться на одинаковом расстоянии от плоскости сравнения, т.е. должны лежать в одной горизонтальной плоскости 0'-0''. Эта плоскость называетсянапорной плоскостью, а геометрическое место вершин вертикальных отрезков на ней – напорной линией.

Из приведенного следует, что уравнение Бернулли для элементарной струйки идеальной жидкости можно определить так: напорная плоскость горизонтальна.

Соединяя плавной кривой верхние концы пьезометрических высот, получим кривую p-p, называемую пьезометрической линией. Падение этой линии на единицу длины струйки называется пьезометрическим уклоном .

Введем сокращенные обозначения для пьезометрической высоты и скоростного напора: h_п = и h_u = .

В этом случае уравнение (5.6) запишется в виде

; (5.7)

Сумму 3-х высот обозначают H_д и называют гидродинамическим или полным напором. Пользуясь этим понятием уравнение (5.7) можно представить в кратчайшей форме H_д = const.

Уравнение Бернулли при некоторых незначительных допущениях может быть распространено и на одномерный поток.

Основная сложность в этом случае состоит в переходе от параметров, определяющих состояние элементарной частицы к параметрам, характеризующим состояние потока в конкретных сечениях.

Для одномерного слабодеформированного потока несжимаемой и невязкой жидкости уравнение Бернулли может быть записано в виде

(5.8)

и – средние скорости в выбранных сечениях;

 – коэффициент, представляющий собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной в предположении, что скорости во всех точках живого сечения равны средней скорости потока (для равномерного турбулентного потока  = 1,0 – 1,13, для ламинарного потока  = 2). Коэффициент  определяется опытным путем.

Величина имеет определенный физический смысл: это средняя удельная энергия потока жидкости, протекающей в единицу времени через выбранное живое сечение.

Таким образом, для описания одномерного установившегося потока идеальной несжимаемой жидкости используются два уравнения:

– уравнение Бернулли, отражающее закон сохранения энергии;

– уравнение неразрывности, отражающее закон сохранения массы.