ЛЕКЦИЯ~1

Лекция 1

Понятие дифференциального уравнения. Порядок дифференциального уравнения. Система дифференциальных уравнений. Задачи, приводящие к дифференциальным уравнениям и системам дифференциальных уравнений.

При решении многих задач механики, физики, техники не удается установить связь между искомой и заданной переменными величинами, а удается установить такую связь между заданной переменной, искомой функцией и ее производными некоторого порядка. При этом возникает дифференциальное уравнение.

Обыкновенным дифференциальным уравнением называется уравнение вида

.

Здесь – независимая переменная, – искомая функция, – заданная функция переменных. Наивысший порядок производной искомой функции , входящей в уравнение, называется порядком дифференциального уравнения.

Иногда требуется определить сразу несколько функций , связанных определенными соотношениями. При этом возникают системы дифференциальных уравнений. В настоящем курсе будут рассмотрены только так называемые нормальные системы дифференциальных уравнений (или системы в нормальной форме)

Порядок нормальной системы определяется количеством ее уравнений.

Рассмотрим некоторые задачи, приводящие к дифференциальным уравнениям и системам дифференциальных уравнений.

Задача 1. Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости вращения. Найти зависимость угловой скорости от времени, если известно, что диск, начавший вращаться со скоростью 5 об./сек. По истечении двух минут вращается со скоростью 3 об./сек.

Обозначим через угловую скорость в момент времени, а через коэффициент пропорциональности. Согласно второму закону Ньютона можем записать

По условию задачи

Задача 2. На покоившееся в начальный момент времени тело массы m начинает действовать линейно возрастающая со временем сила , где – постоянный вектор. Найти смещение тела от начального положения, если сила сопротивления среды пропорциональна скорости:

Воспользовавшись законом Ньютона, можем записать следующие векторные соотношения:

Если в полученных соотношениях перейти к покоординатной записи, то придем к нормальной системе трех дифференциальных уравнений.

Задача 3. Тело совершает движение под действием двух пружин. Восстанавливающая сила пропорциональна смещению тела. Найти закон движения тела, если: а) движение совершается в вакууме, б) движение совершается в сопротивляющейся среде, причем сила сопротивления пропорциональна скорости, в) движение совершается в сопротивляющейся среде, но на тело действует гармоническая возмущающая сила

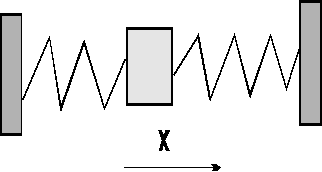
Пусть – величина смещения тела от положения равновесия в момент времени t. Пользуясь вторым законом Ньютона и законом Гука, можем записать уравнения движения для каждого из перечисленных выше случаев:

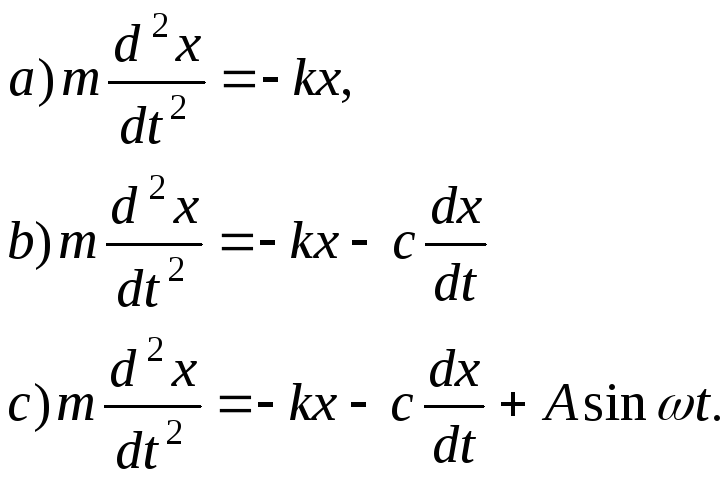
Такими же уравнениями описываются малые колебания маятника, электрические колебания в контуре, содержащем емкость и индуктивность.

Задача 4. Рассмотрим горизонтально расположенную балку постоянного поперечного сечения, сделанную из однородного материала. Под влиянием сил, которые действуют на балку в вертикальной плоскости, содержащей ее ось симметрии, балка может изгибаться. Действующие силы могут быть обусловлены весом балки, внешней нагрузкой или обеими силами вместе. Искривленная ось симметрии – упругая линия. Определение ее формы очень важно в теории упругости.

Ставится следующая задача: однородная горизонтальная балка, свободно лежащая на двух опорах, прогибается под действием собственного веса, равного Р килограммов на единицу длины. Требуется найти уравнение упругой линии и максимальный прогиб балки.

Введем систему координат ОXY в плоскости прогиба оси балки и будем считать, что балка, имеющая длину l, расположена вдоль оси ОХ. Из теории сопротивления материалов известно, что изгибающий момент М(х) в точке с абсциссой х связан с радиусом кривизны упругой линии в этой точке соотношением

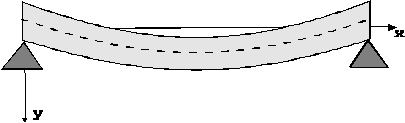
где Е – модуль упругости Юнга, I – момент инерции поперечного сечения балки. Можно показать, что для поставленной задачи . Если считать, что прогиб балки мал, то производная мала и уравнение примет вид

Мы пришли к так называемой краевой задаче.

Задача 5. Рассмотрим двойной маятник, совершающий малые колебания относительно точки подвеса.

Можно показать, что уравнения таких колебаний имеют вид:

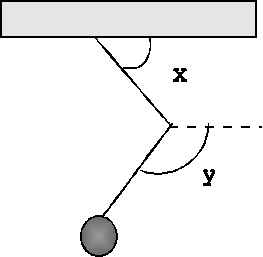
Вводя обозначения , получим

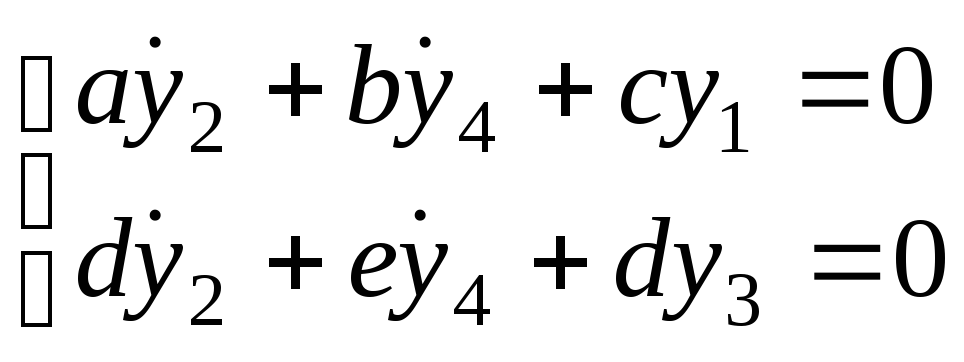или

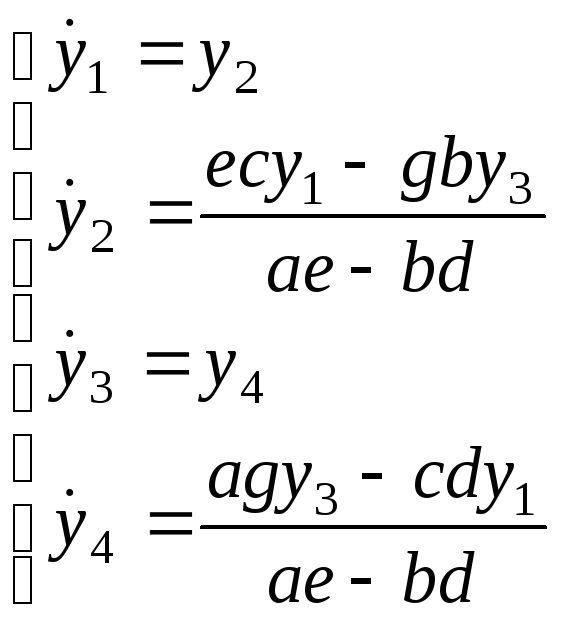
Пришли к нормальной системе дифференциальных уравнений четвертого порядка.

Задача 6.Регулирование курса судна автоматическим рулевым осуществляется по схеме:

Руль Судно



Курс

Судно должно устойчиво следовать курсу, то есть при малых отклонениях от курса ( мало) с малыми скоростями ( мало) авторулевой должен возвращать судно на курс.

Математическая модель системы судно-авторулевой представляет собой следующую систему дифференциальных уравнений

.

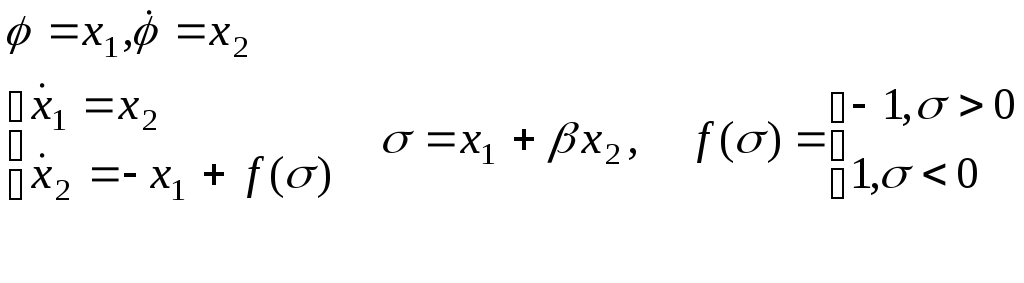Судно будет возвращаться на курс при малых отклонениях от него в том случае, когда состояние равновесия приведенной системы устойчиво в малом.

Дифференциальное уравнение первого порядка. Задача Коши.

Дифференциальным уравнением первого порядка называется уравнение вида

(1)

Уравнение (1) называют уравнением, не разрешенным относительно производной. Если из этого уравнения удается выразить , то получим уравнение

. (2)

Это уравнение разрешенное относительно производной.

Определение. Дифференцируемая на интервале (,) функция у(х) называется решением уравнения (1), если на этом интервале.

График функции у(х) на (,) называется интегральной кривой дифференциального уравнения.

На примере простейшего уравнения видно, что оно имеет бесконечно много решений . Для того, чтобы из этого множества решений выделить какое-либо одно (из множества интегральных кривых выделить одну), необходимо задать точку , через которую проходит интегральная кривая. Иными словами, нужно потребовать, чтобы

(3)

Задача отыскания решения уравнения (2), удовлетворяющего условию (3) называется задачей Коши.

Фундаментальным результатом теории обыкновенных дифференциальных уравнений является следующая теорема.

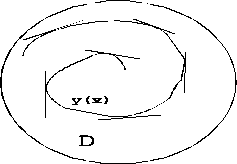
Теорема Коши (теорема существования и единственности решения). Пусть функция и ее частная производная непрерывны в некоторой области D на плоскости ОХУ, содержащей точку . Тогда

1. в некоторой окрестност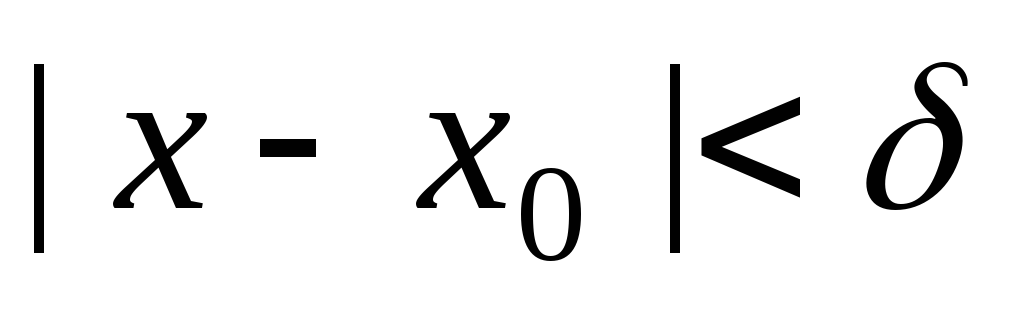и точки 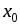существует решение задачи Коши (2) - (3).

2. Если 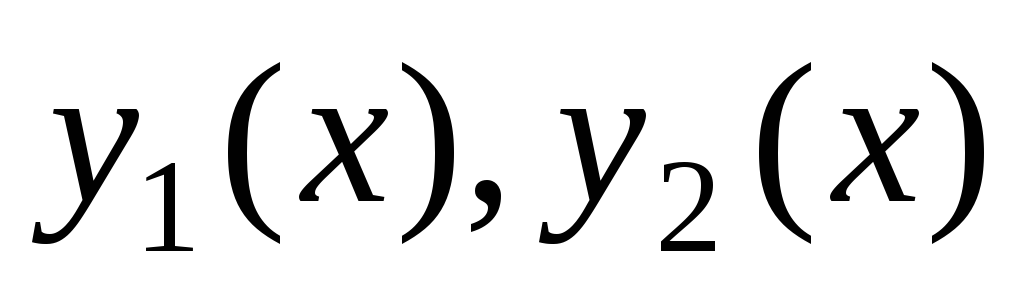– два решения уравнения (2), удовлетворяющие начальному условию (3), то 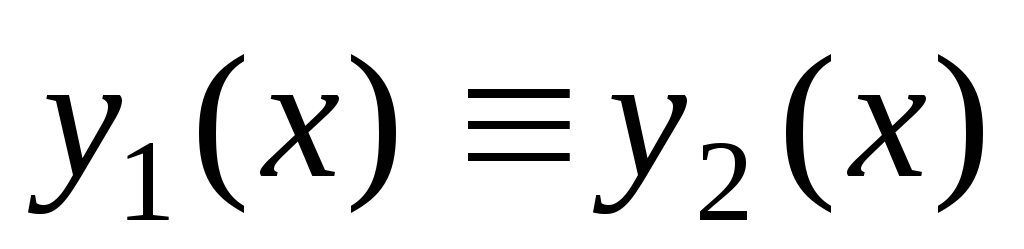при всех тех значениях х, при которых оба этих решения определены.

Теорема Коши имеет простую геометрическую интерпретацию. Ее можно сформулировать так: если условия теоремы Коши выполнены, то через каждую точку проходит интегральная кривая уравнения (2) и притом только одна.

Доказательство теоремы Коши будет дано ниже.

Из теоремы Коши следует, что уравнение (2) имеет бесконечно много решений. Семейство решений зависит от одного параметра . Таким образом, область «расслаивается» на интегральные кривые.

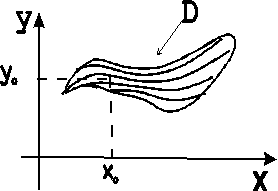
Каждая из этих кривых проходит таким образом, что угловой коэффициент касательной к ней в любой ее точке равен значению функции в этой точке. То есть в произвольной точке задано направление касательной к интегральной кривой, проходящей через эту точку. Множество направлений касательных образуют поле направлений уравнения (2) в D. Построив это поле, можно нарисовать интегральные кривые уравнения (2). Для удобства построения поля направлений применяют метод

изоклин.

Изоклины – линии на плоскости ОХУ, задаваемые уравнением В каждой точке изоклины касательные к интегральным кривым имеют один и тот же наклон к оси ОХ. Построив семейство изоклин можно приближенно графически проинтегрировать дифференциальное уравнение.

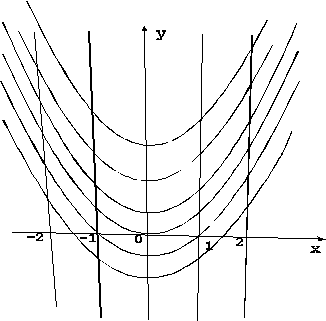
Продемонстрируем этот метод на примере уравнения Полагая поочередно , построим поле направлений и приближено построим интегральные кривые уравнения.

6