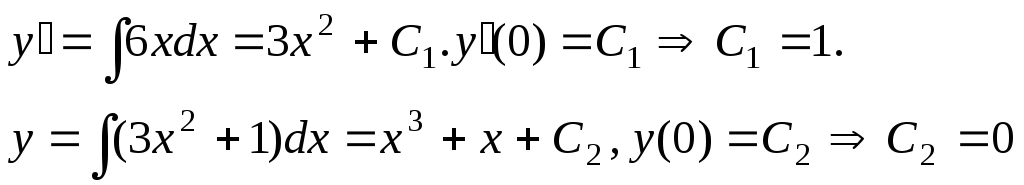Лекция 6

Зависимость решений от начальных данных и параметров

В реальных задачах, связанных с решением дифференциальных уравнений, начальные значения обычно известны лишь с некоторым приближением, поскольку они определяются экспериментально или вычисляются, что неизбежно связано с появлением погрешностей. Кроме того, в правые части уравнений могут входить параметры, характеризующие физическую природу изучаемой системы (масса, заряд, упругость), которые тоже определяются приближенно. В связи с этим возникает вопрос о том, как изменяется решение задачи при небольших изменениях начальных значений и параметров и зависит ли оно от этих значений непрерывно.

Рассмотрим задачу Коши

(1)

где – параметр. Пусть – область в пространстве .

Теорема 1. Если непрерывны в по совокупности переменных и , то решение задачи (1) непрерывно по совокупности переменных в некоторой области .

Теорема утверждает, что интегральные кривые, проходящие через точку и соответствующие различным близким значениям параметра , будут близки.

Задача о зависимости решений от начальных данных может быть сведена к задаче о зависимости решений от параметров путем замены переменных. Действительно, полагая, преобразуем уравнение к виду

. (2)

Теперь и играют роль параметров. Если непрерывная вместе со своей частной производной функция, то к системе (2) может быть применена теорема о непрерывной зависимости от параметров и . Можно сформулировать следующий результат для семейства задач Коши

. (3)

Теорема 2. Пусть решения 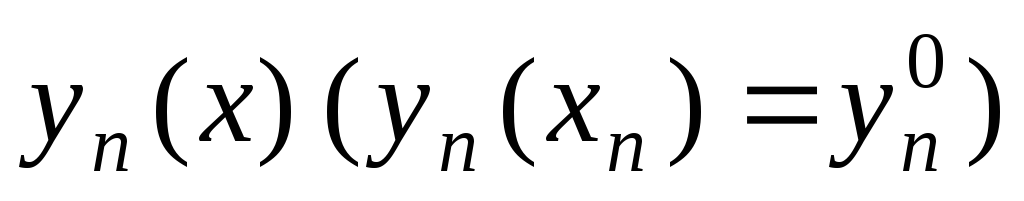задач (3) определены на отрезке 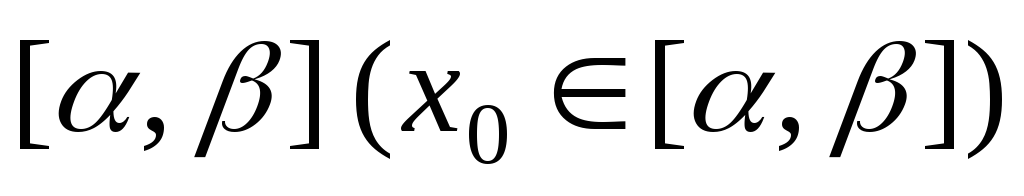. Тогда последовательность 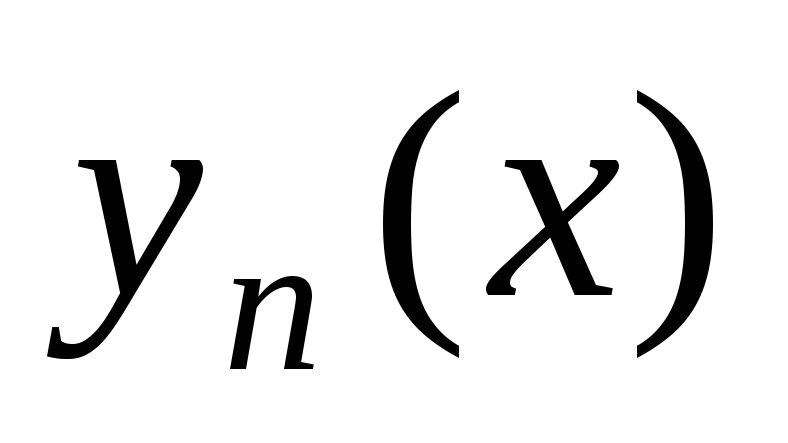на 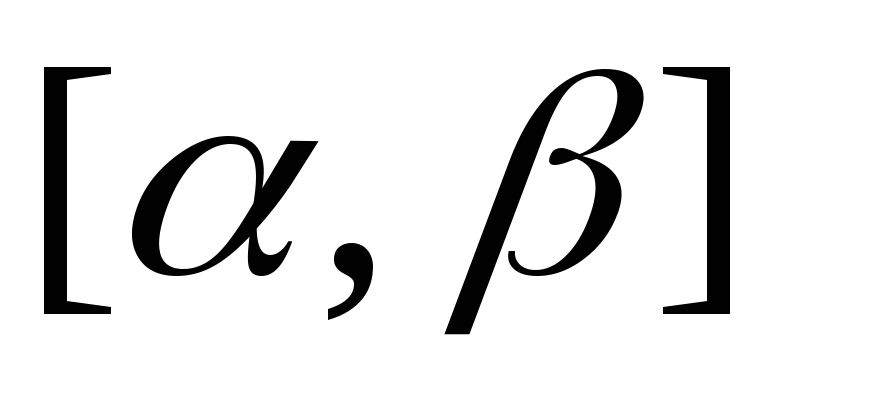равномерно сходится к , где 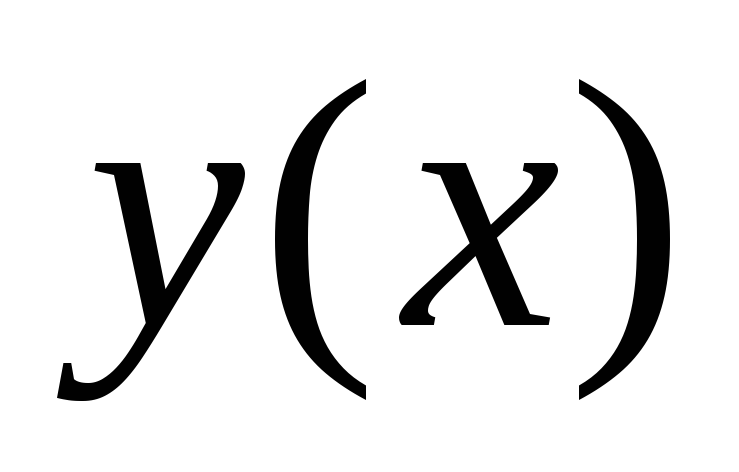– решение задачи .

Теорема утверждает, что решения задачи Коши с близкими начальными условиями будут близки при всех тех , при которых все они определены.

Дифференциальные уравнения -го порядка

Дифференциальное уравнение вида

называется дифференциальным уравнением -го порядка не разрешенным относительно старшей производной. Если удается разрешить его относительно , то получаем

. (4)

Теорема (существования и единственности решения). Пусть функция , рассматриваемая как функция переменной, непрерывна в некоторой области , содержащей точку , вместе со своими частными производными . Тогда существует интервал и определенная на нем раз дифференцируемая функция , удовлетворяющая уравнению (4) и начальным условиям

. (5)

Функция 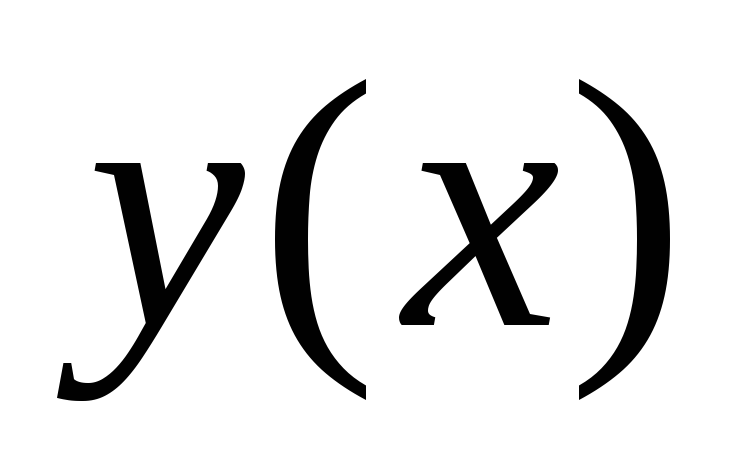, обладающая указанными свойствами, единственна.

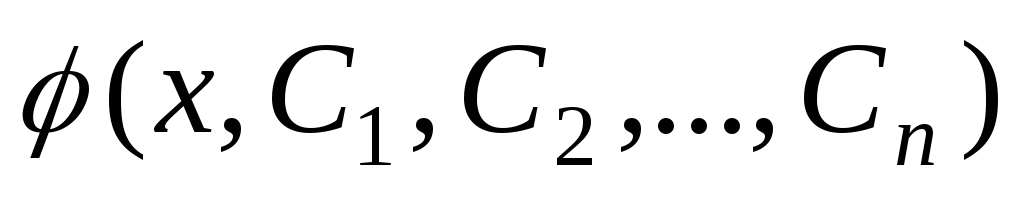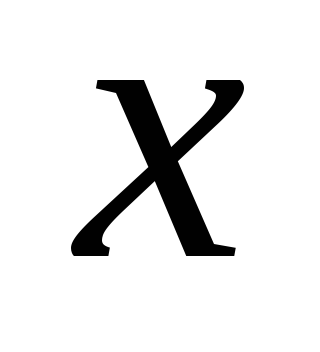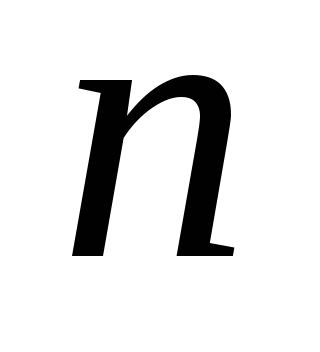Определение. Общим решением уравнения (4) называется функция , зависящая от и произвольных постоянных 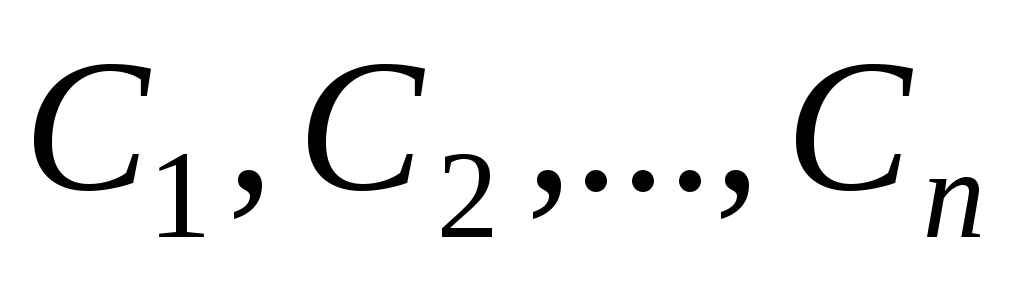, такая, что

1. для любых значений произвольных постоянных 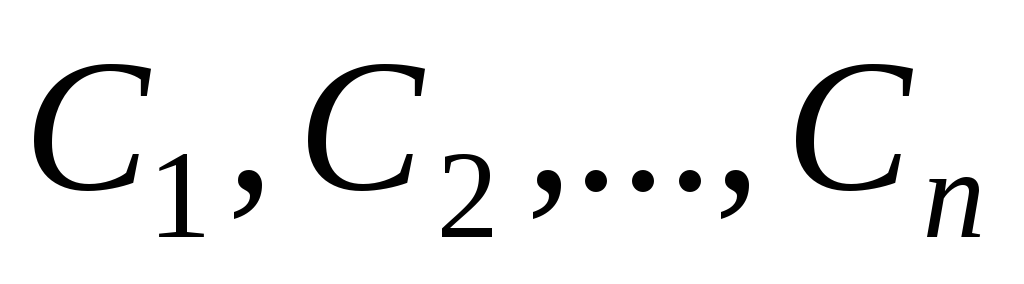функция 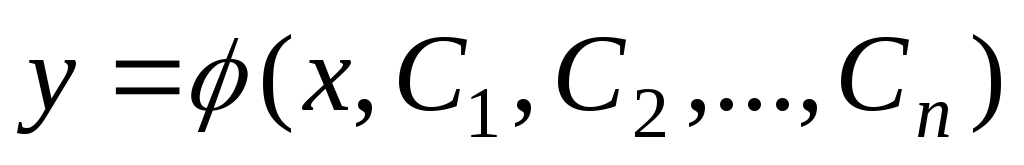есть решение уравнения (4),

2. существуют единственные значения 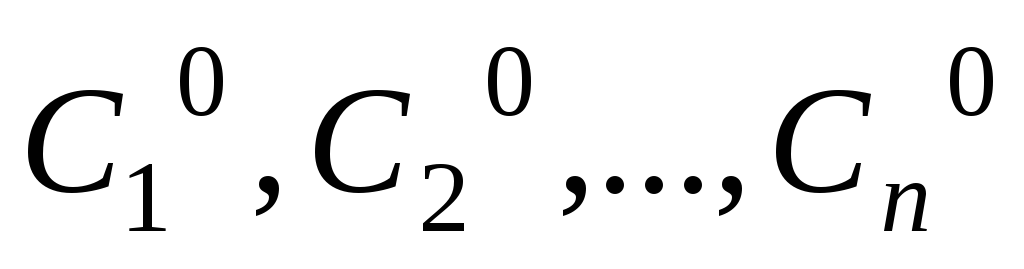такие, что

есть решение уравнения (4), удовлетворяющее начальному условию (5).

Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка

Не существует общих приемов, позволяющих проинтегрировать произвольное дифференциальное уравнение высшего порядка. Однако в некоторых случаях порядок дифференциального уравнения может быть понижен и его решение может быть сведено к последовательному интегрированию нескольких дифференциальных уравнений первого порядка. Остановимся на этих случаях.

I.Решение уравнения вида сводится к кратному интегрированию.

Пример. Среди интегральных кривых уравнения найти ту, которая в начале координат касается прямой .

Необходимо найти решение уравнения 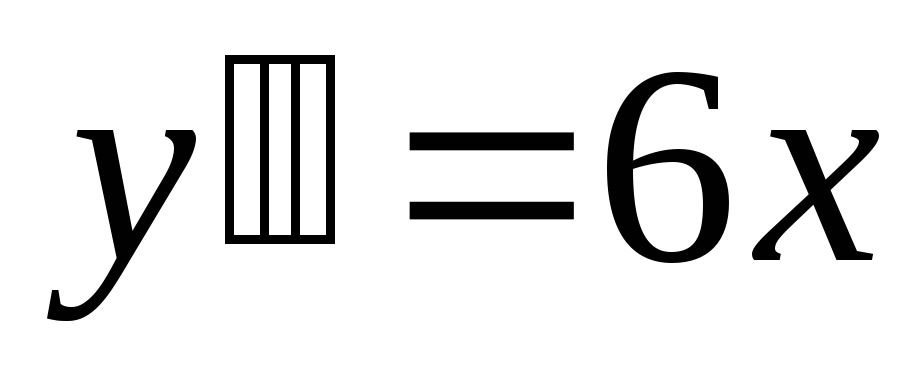, удовлетворяющее начальным условиям 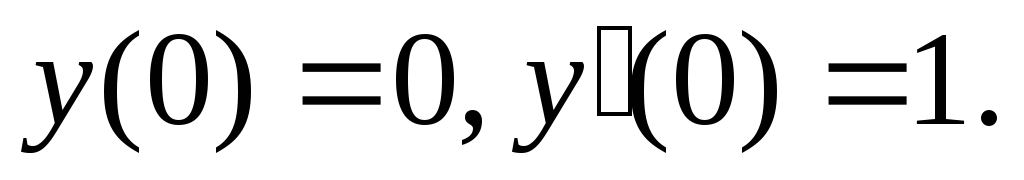Последовательно интегрируя и подставляя заданные начальные условия, получим

Итак, искомая интегральная кривая

II.Уравнение не содержит и его производных до порядка включительно: .

Для понижения порядка уравнения применяется подстановка . После применения этой подстановки уравнение приобретает вид . Если удается найти общее решение последнего уравнения , то после -кратного интегрирования получим общее решение исходного уравнения.

Пример. Проинтегрировать уравнение .

Выполним замену Тогда получим уравнение . Разрешив последнее уравнение относительно , будем иметь . Введем параметр после чего продифференцируем обе части уравнения по

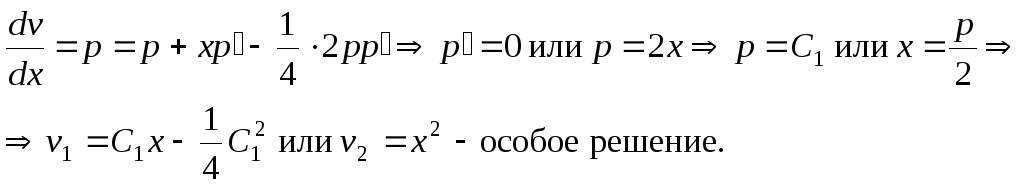
Для имеем . Полагая , запишем полученное решение в виде .

Для – особое решение.

III.Уравнение не содержит явно переменной : . В этом случае порядок уравнения понижается путем замены . Последовательно получим

.

Приходим к уравнению -го порядка

Е сли удалось найти общее решение последнего уравнения , то для отыскания будем иметь уравнение с разделяющимися переменными

.

Пример. Найти общее решение уравнения .

Последовательно получаем

.

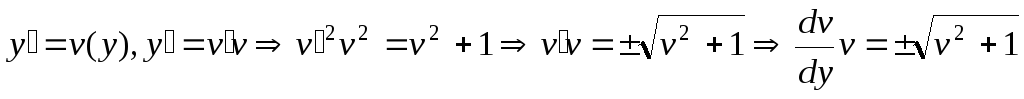
Это уравнение может быть разрешено относительно . Полагая , получим

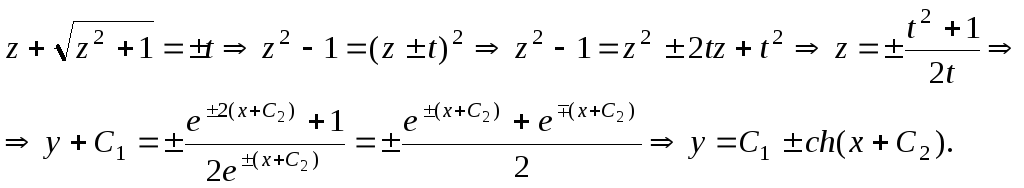
IY. Уравнение однородное относительно и его производных. Однородным называется уравнение , для которого выполнено

.

Порядок однородного уравнения понижается путем введения новой переменной по правилу . Тогда получим

.

При этом исходное уравнение принимает вид

.

Пусть найдено его решение . Для нахождения получаем уравнение с разделяющимися переменными , решение которого имеет вид . Заметим, что решение нами не потеряно. Оно получается из последней формулы при .

Пример. Найти общее решение уравнения .

Уравнение однородное относительно и его производных. Поэтому положим

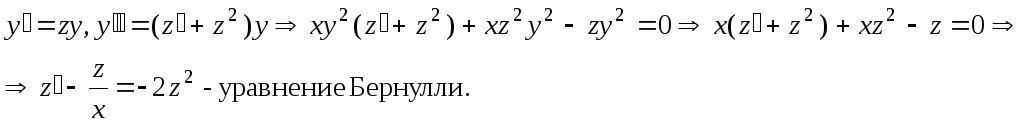
Применяя метод Бернулли, решим это уравнение.

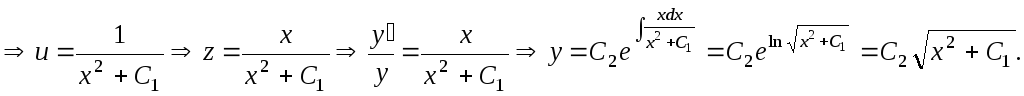
Замечание. При интегрировании данного уравнения нами потеряно решение . В результате потеряно решение исходного уравнения, которое не содержится в найденном общем решении.

В заключение остановимся еще на одном приеме интегрирования уравнений высшего порядка, позволяющем понизить порядок решаемого уравнения.

Пусть уравнение имеет вид . Иными словами, левая часть этого уравнения представляет собой полную производную по от некоторой функции . Интегрируя обе части такого уравнения по , получим новое уравнение , порядок которого на единицу меньше, чем у исходного.

Пример. Найти общее решение уравнения

Левая часть этого уравнения есть полная производная от функции , а правая от функции . То есть уравнению можно придать вид . Интегрируя обе части по переменной , получим , или

Окончательно получаем

5