1. Площадь поверхности в r3

Поверхность в задается параметрически при помощи 2 параметров

,

,

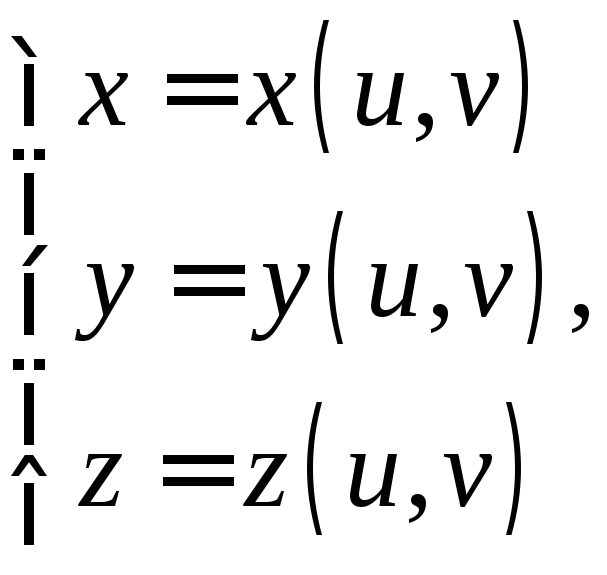
- поверхность в .

Иногда поверхность задают при помощи одной функции двух переменных

.

Тогда параметрическое задание имеет вид

.

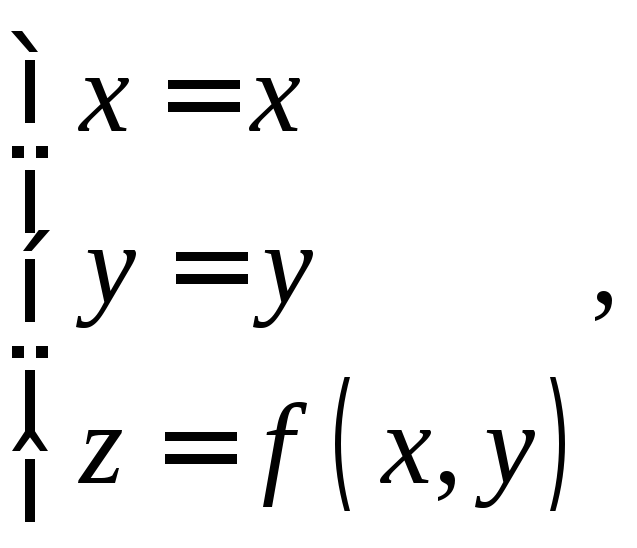
Поверхность называется гладкой, если

.

Из этих частных производных можно записать матрицу Якоби нашего отображения

.

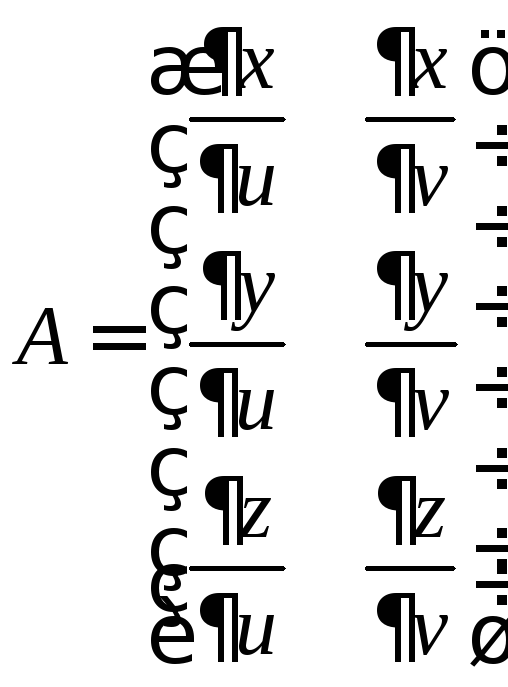Точку назовем не особой, если ранг матрицы А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно независимыми.

Выясним геометрический смысл этих векторов. Эти векторы - касательные векторы к линиямна поверхности. В не особой точке эти касательные векторы не коллинеарные.

Можно показать, что все касательные векторы к кривым на поверхности, проходящие через , лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке.

В не особой точке уравнение касательной плоскости можно записать с помощью точки и двух касательных векторов:

.

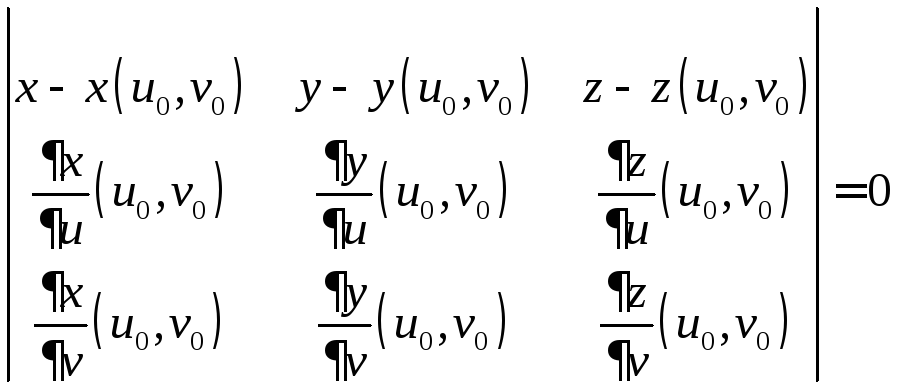Рассмотрим вектор .

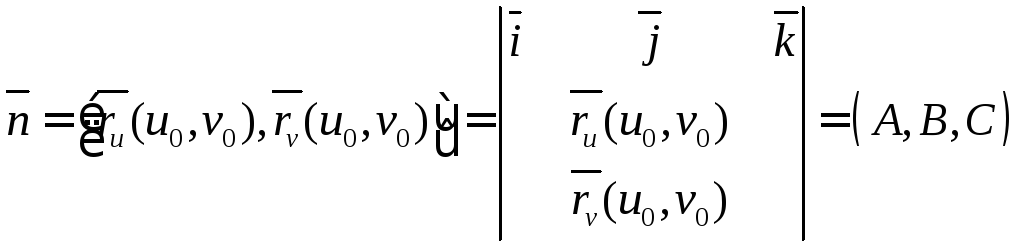Очень часто в качестве нормального вектора будем использовать единичный нормальный вектор

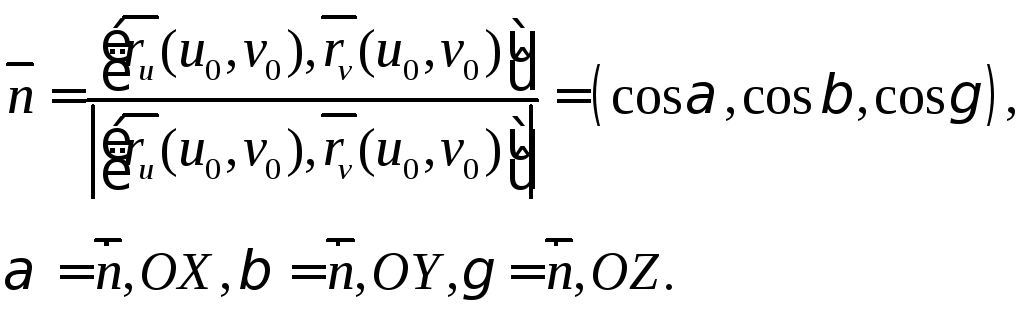
Определим первую квадратную форму на поверхности. Пусть

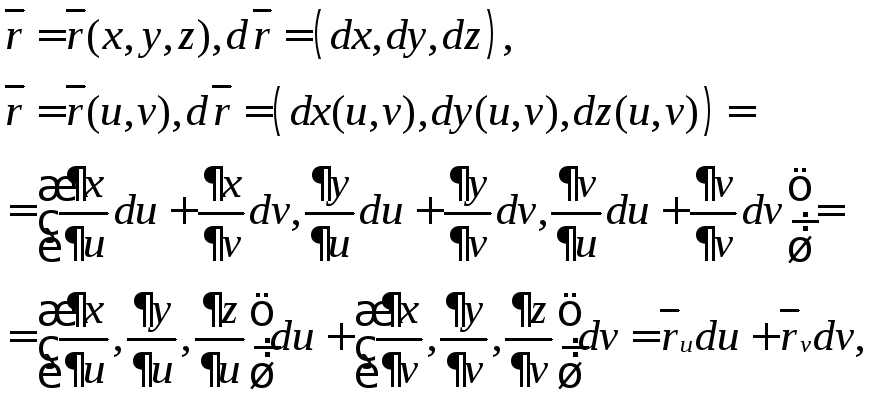
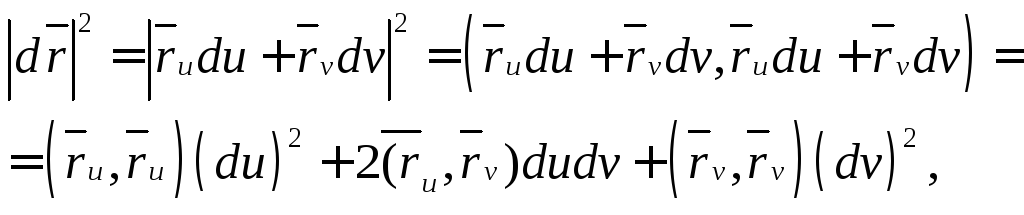
Таким образом, первая квадратичная форма на поверхности имеет вид: .

Определение. Площадью гладкой поверхности ,-измеримо по Жордану, называется число:.

Преобразуем эту формулу для площади поверхности

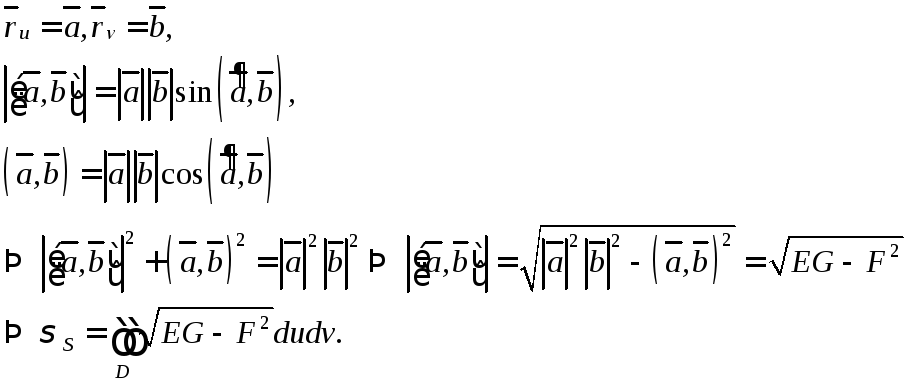
2. Поверхностный интеграл 1-го рода. Его свойства, вычисление

Пусть поверхность ,

- непрерывная функция.

Определение. Поверхностным интегралом первого рода по поверхности от функции называется число

.

Здесь - элемент площади поверхности.

Данное определение справедливо и для кусочно-гладкой поверхности, т.е. поверхности, которая может быть разбита на конечное число гладких участков.

Поверхностный интеграл первого рода сводится к некоторому двойному интегралу и для него справедливы все его свойства.

3. Приложения поверхностного интеграла 1-го рода

Геометрическое приложение: Вычисление площади поверхности

Механические приложения: Вычисление массы, статических моментов, координат центра тяжести поверхности, начиненной веществом с плотностью .

Масса: .

Первые статические моменты относительно координатных плоскостей:

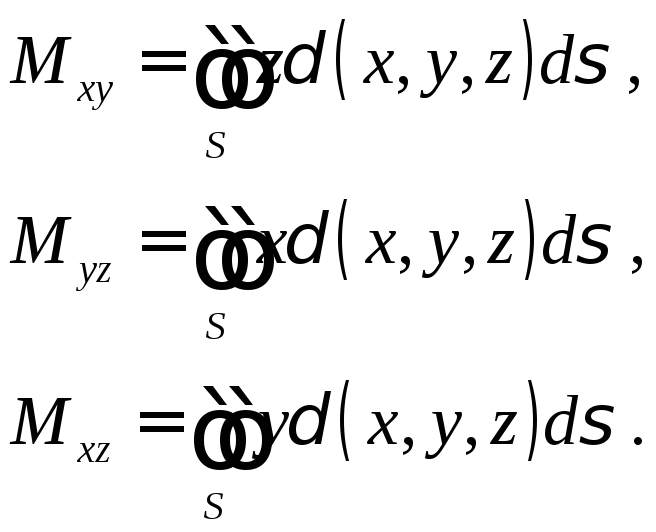
Координаты центра тяжести:

.

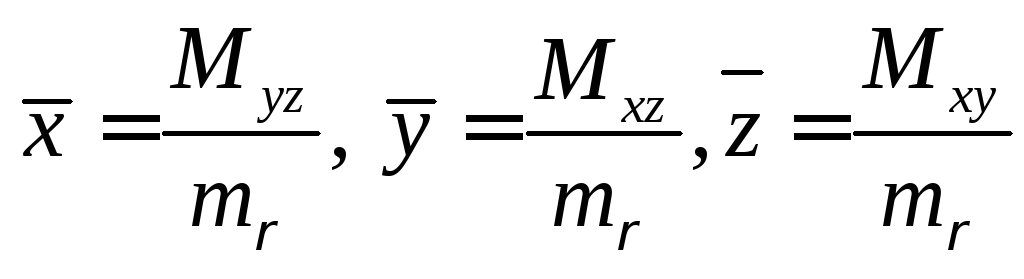Вторые статические моменты относительно координатных плоскостей:

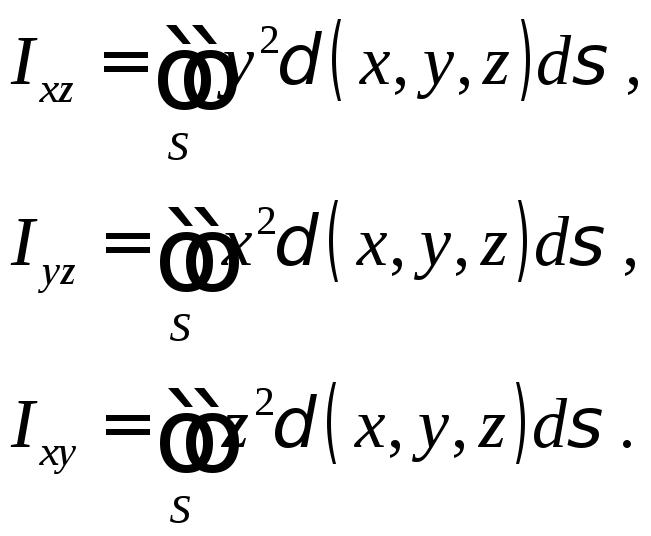
Статический момент (момент инерции) относительно начала координат:

.

ЛЕКЦИЯ 18

Поверхностный интеграл 2-го рода. Его связь с поверхностным интегралом 1-го рода. Теорема Гаусса-Остроградского

1. Поверхностный интеграл 2-го рода.

Будем рассматривать гладкие двусторонние поверхности. Сторона выбирается с помощью нормали к поверхности.

Пусть некоторая двусторонняя поверхность,- векторное поле на поверхности. Нам необходимо определить поверхностный интеграл второго рода по какой-то стороне поверхностидля векторного поля. Этот интеграл запишется следующим образом:

.

Определим интеграл . Остальные интегралы будут определяться аналогично.

Пусть . Стороны на этой поверхности можно выбирать следующим образом:

- это сторона поверхности, нормаль к которой образует с осью острый угол;

- это сторона поверхности, нормаль к которой образует с осью тупой угол.

В таком случае положим

.

Физический смысл поверхностного интеграла 2-го рода – вычисление потока векторного поля через поверхностьв направлении нормали.