
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
2. Сферические координаты в Rn. Их ортогональность
Сферические
координаты в
![]() задаются отображением
задаются отображением
![]() ,
,
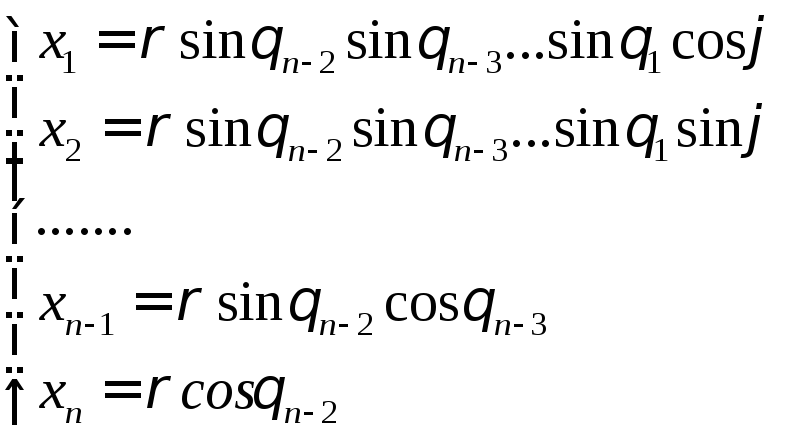 .
.
Найдем касательные векторы и коэффициенты Ламе
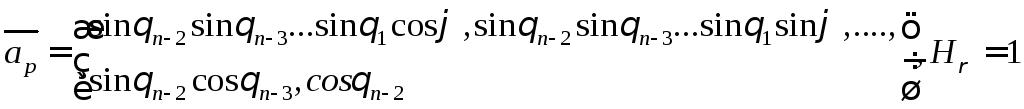
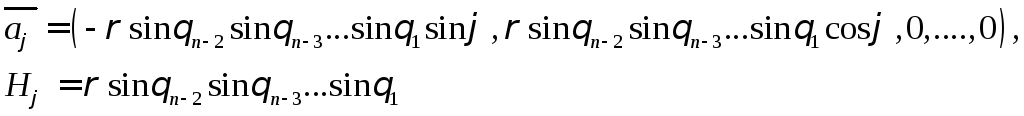
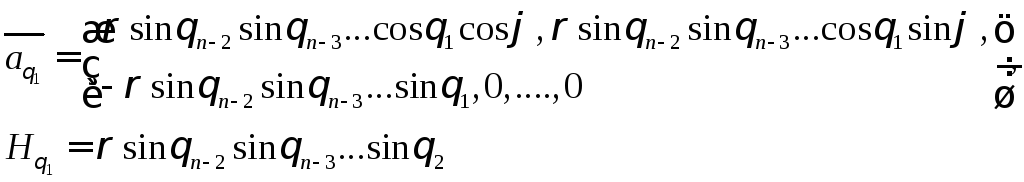
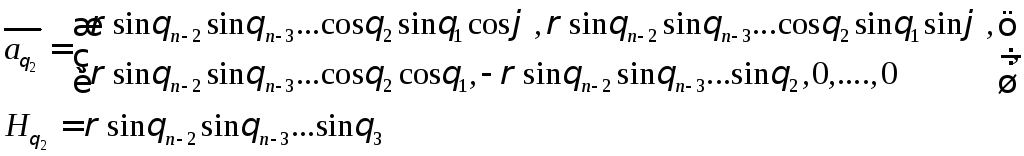
………….
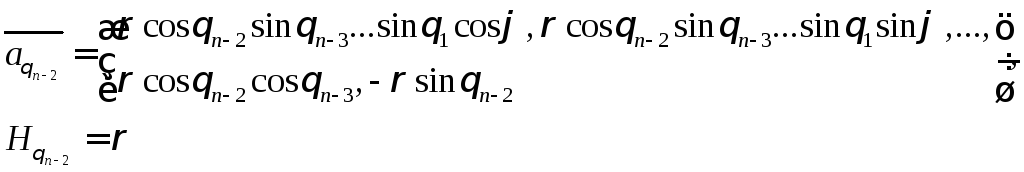
Убеждаемся в ортогональности сферических координат и вычисляем Якобиан:
![]() ,
,
![]() .
.
3.
Вычисление объема
![]() n-мерного
шара
n-мерного
шара
Имеем
![]() -
объем шара радиуса
-
объем шара радиуса
![]() .
Переход к повторному интегралу дает
.
Переход к повторному интегралу дает
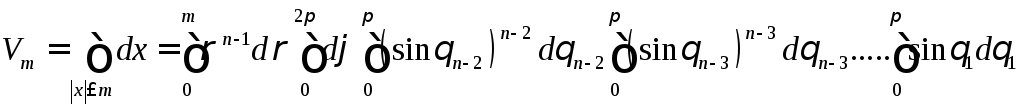 .
.
Пусть
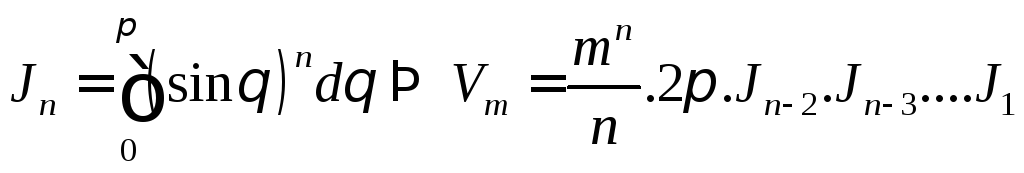 .
Получим рекуррентную формулу для
.
Получим рекуррентную формулу для![]() :
:
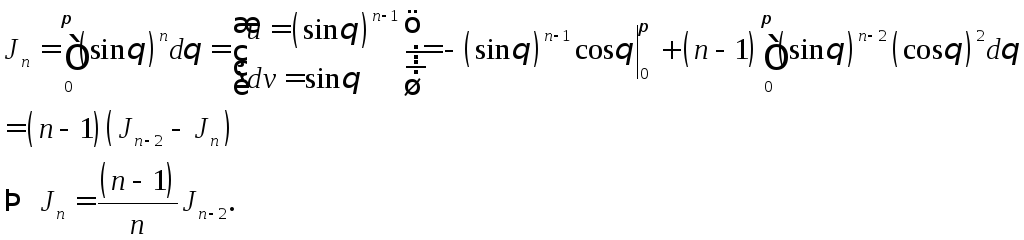 Разбирая
различные случаи, получим
Разбирая
различные случаи, получим
если
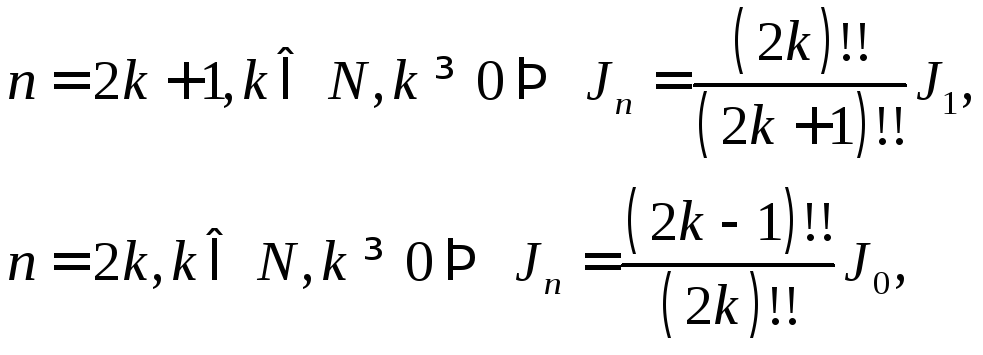
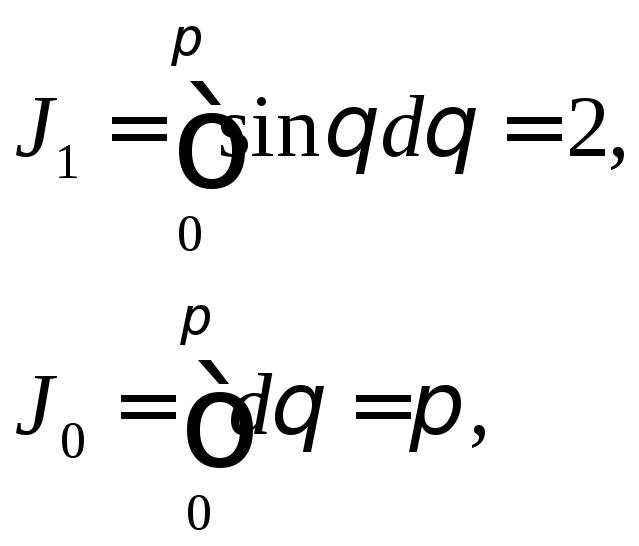
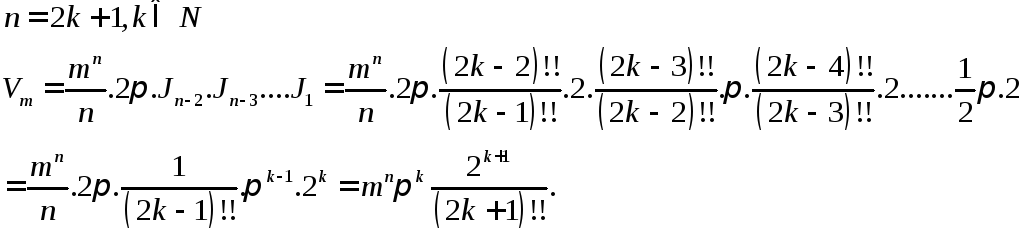
Имеем
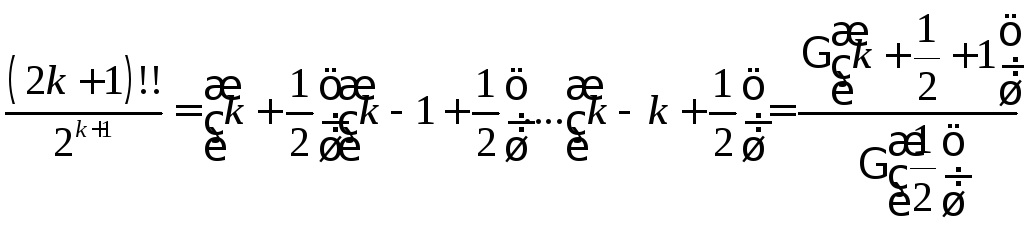
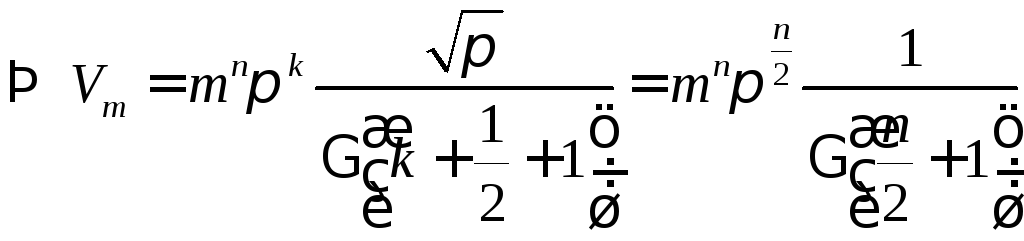 ,
,
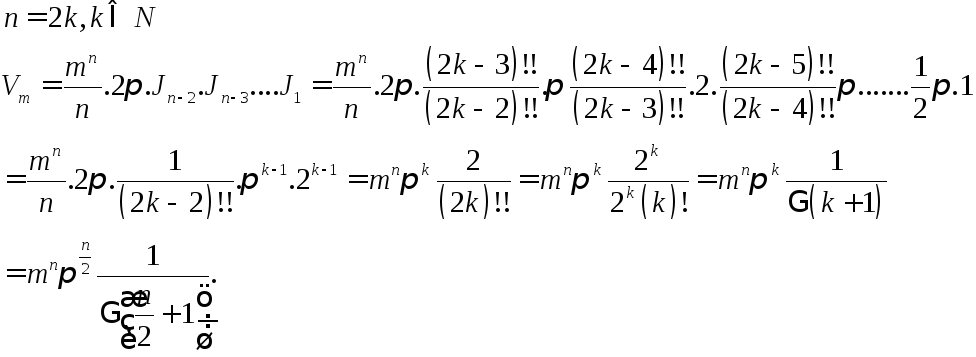
ЛЕКЦИЯ 12
Оператор Лапласа в ортогональных координатах. Оператор Лапласа в полярных координатах в R2, цилиндрических и сферических
координатах в R3
1. Оператор Лапласа в ортогональных координатах
Дифференциальный
оператор Лапласа второго порядка
![]() задается равенством
задается равенством
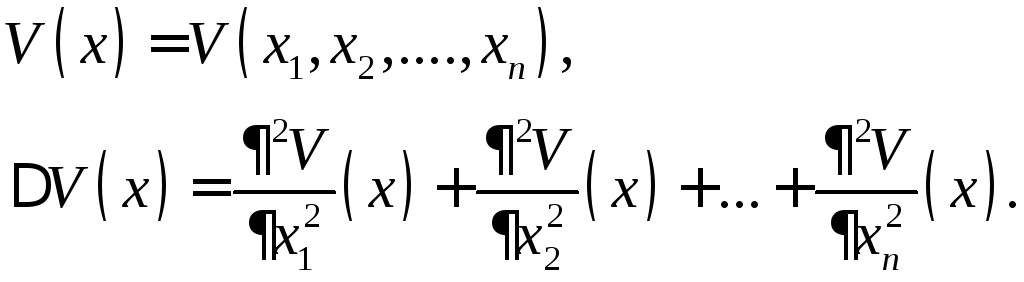
Тогда
![]() -
уравнение Лапласа.
-
уравнение Лапласа.
Если
![]() - ортогональные координаты, то оператор
Лапласа в новых координат примет
следующий вид :
- ортогональные координаты, то оператор
Лапласа в новых координат примет
следующий вид :
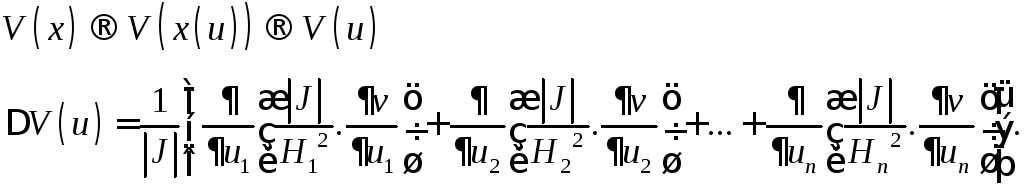
2. Оператор Лапласа в полярных координатах в R2, цилиндрических и сферических координатах в R3
Оператор
Лапласа в полярных координатах в
![]() :
:
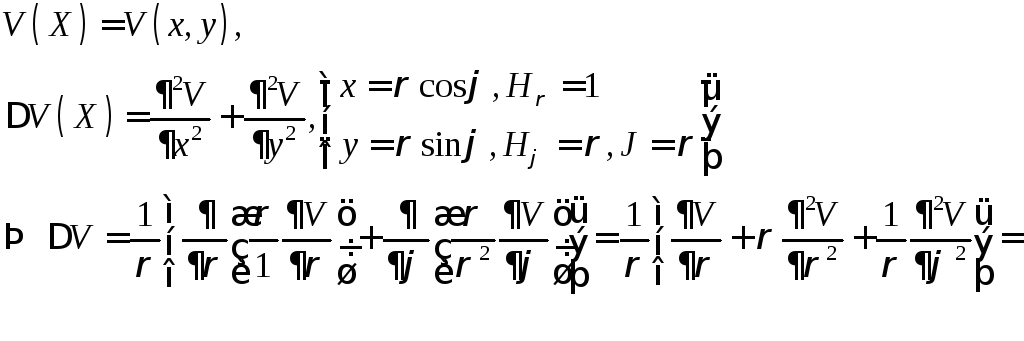
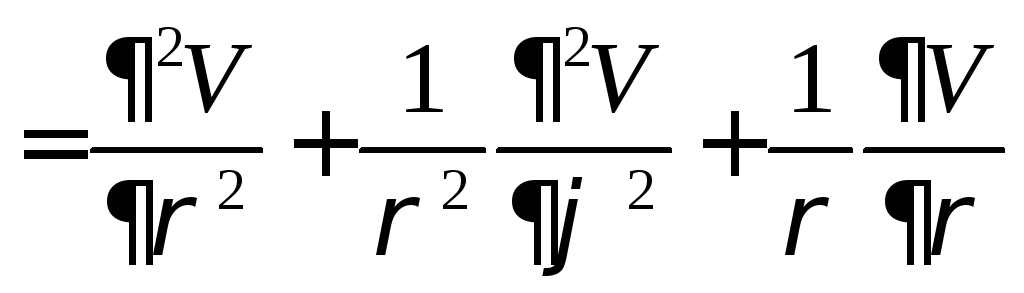 .
.
Оператор Лапласа в цилиндрических координатах:
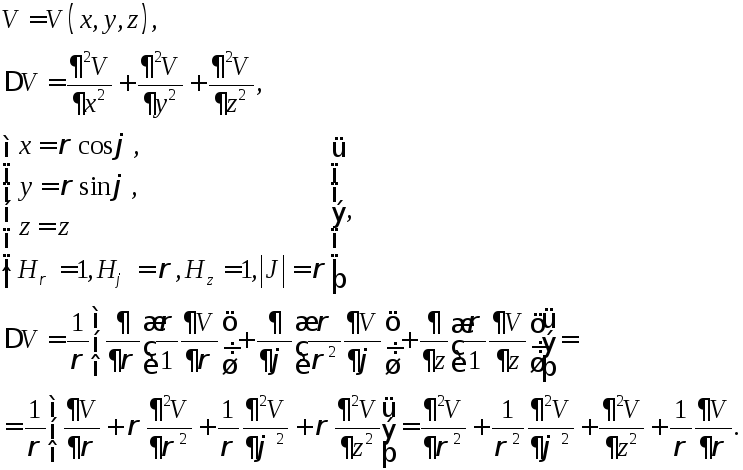
Оператор Лапласа в сферических координатах:
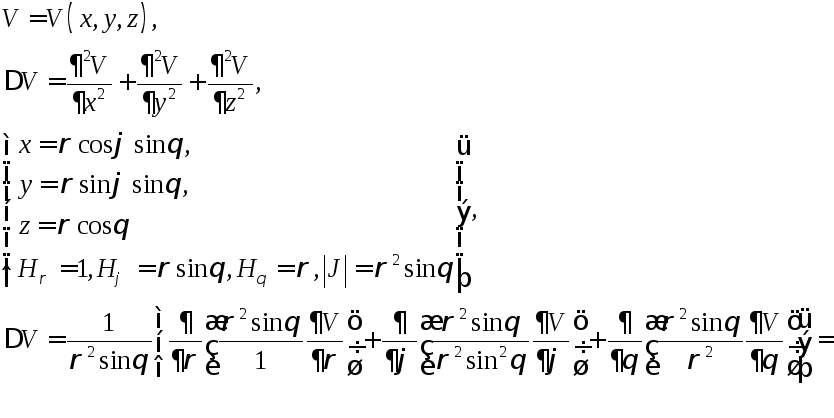
ЛЕКЦИЯ 13
Кратные
несобственные интегралы 1-го и 2-го рода.
Абсолютная сходимость. Признак сравнения.
Сходимость кратных интегралов
![]()
1. Кратные несобственные интегралы 1-го. Абсолютная сходимость.
Признак сравнения
Пусть
![]() -
неограниченная область,
-
неограниченная область,
![]() ,
,
![]() ,
,![]() для любого
для любого![]() .
.
Последовательность
множеств
![]() из
из![]() называется
называется![]() -допустимой,
если
-допустимой,
если
1.
![]() ограничены, измеримы по Жордану,
ограничены, измеримы по Жордану,
2.
![]() ,
,![]() ,
,
3.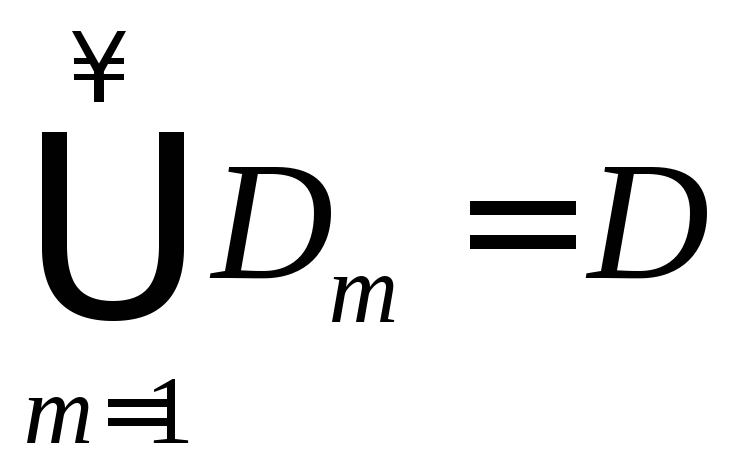 .
.
Пример
:
![]() ,
,![]() -допустимой
последовательностью будет, например,
последовательность шаров
-допустимой
последовательностью будет, например,
последовательность шаров![]() .
.
Число
![]() называется несобственным интегралом
первого рода от функции
называется несобственным интегралом
первого рода от функции![]() по неограниченной области, если для
любой последовательности
по неограниченной области, если для
любой последовательности![]() ,
,![]() -допустимых
множеств, существует
-допустимых
множеств, существует![]() .
.
В
случае сходимости значение несобственного
интеграла полагается равным
![]()
Если
сходится интеграл
![]() ,то говорят,
что интеграл
,то говорят,
что интеграл
![]() сходится абсолютно.
сходится абсолютно.
Теорема.
Несобственный
интеграл
![]() сходится
сходится![]()
![]() -
сходится.
-
сходится.
Интеграл
![]() сходится
сходится
![]() последовательность
последовательность![]() ограниченная хотя бы для одной
последовательности
ограниченная хотя бы для одной
последовательности![]() -допустимых
множеств.
-допустимых
множеств.
Эта теорема указывает на большую разницу между одномерным и многомерным случаями.
Признак сравнения можно записать в следующей форме.
Теорема.
Пусть функции
![]() интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве
интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве
![]() и
и![]() .
Тогда
.
Тогда
если несобственный интеграл
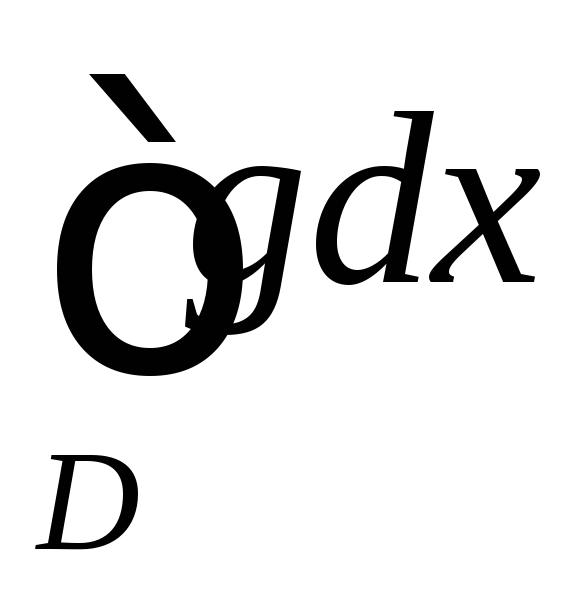 сходится, то несобственный интеграл
тоже
сходится, то несобственный интеграл
тоже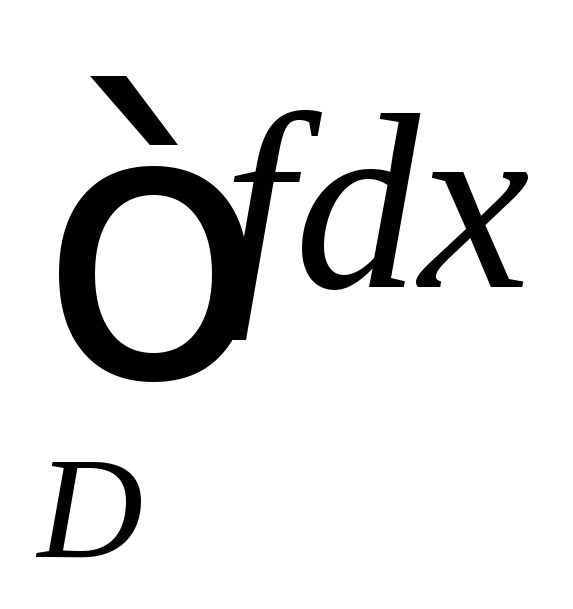 сходится;
сходится;если несобственный интеграл
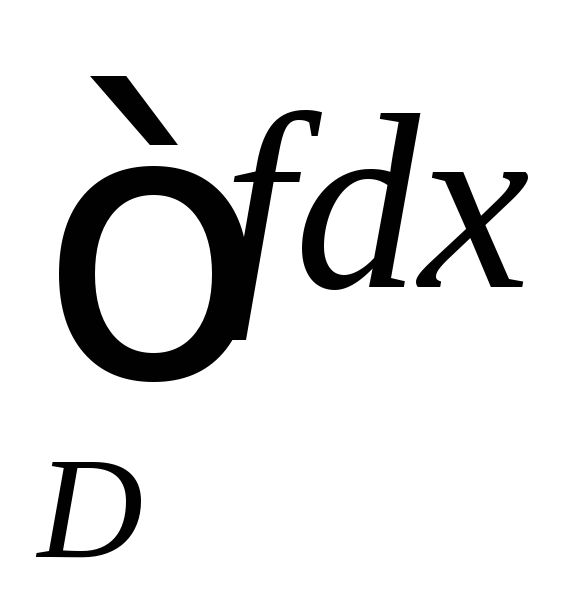 расходится, то несобственный интеграл
расходится, то несобственный интеграл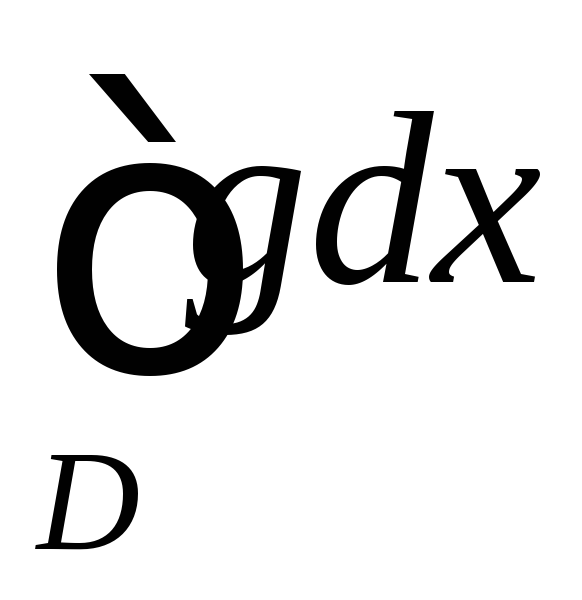 тоже расходится.
тоже расходится.
2. Сходимость кратных интегралов
Рассмотрим несобственный интеграл
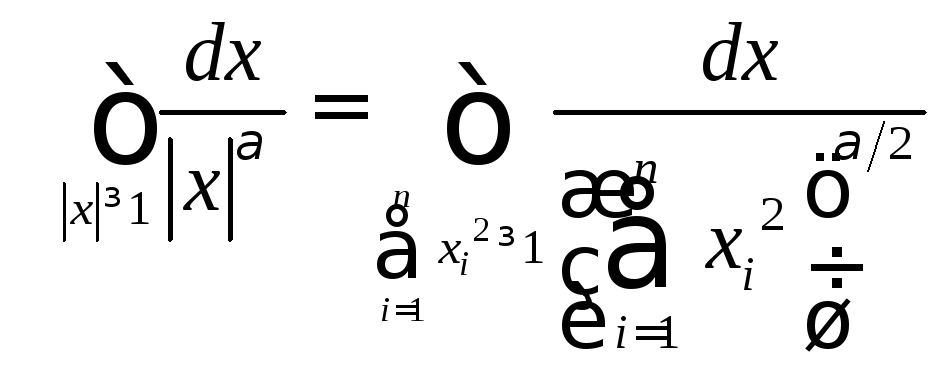 .
.
При
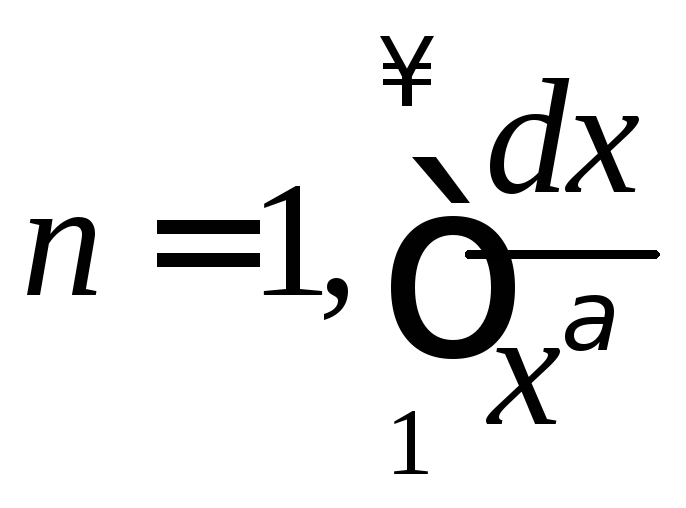 -
сходится при
-
сходится при![]() и расходится при
и расходится при![]() .
.
При
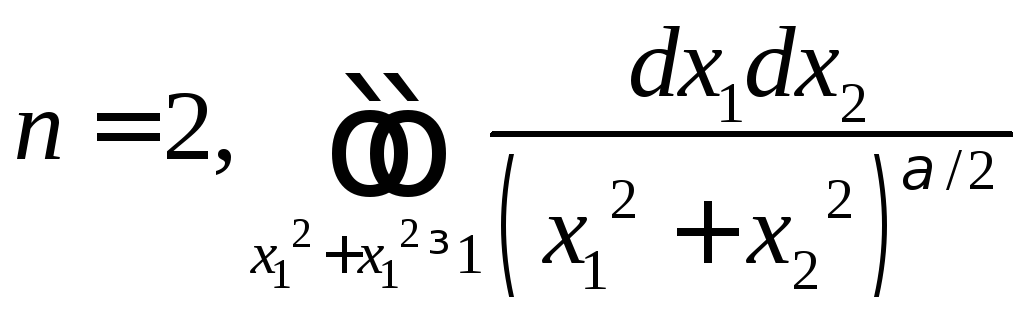 ,
,
![]() .
.
В
полярной системе координат
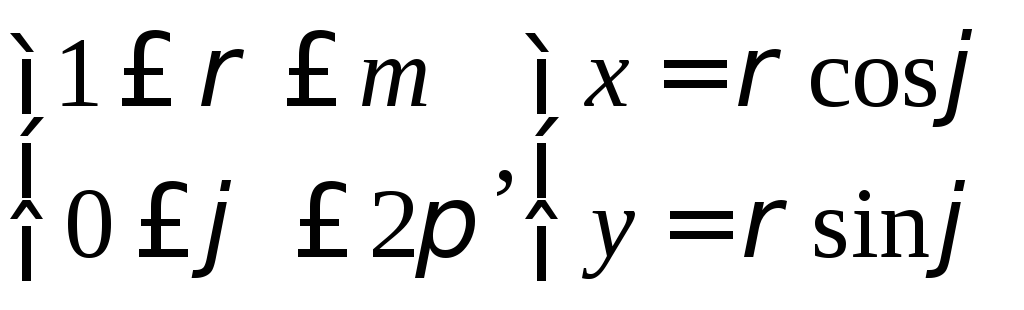 ,
,
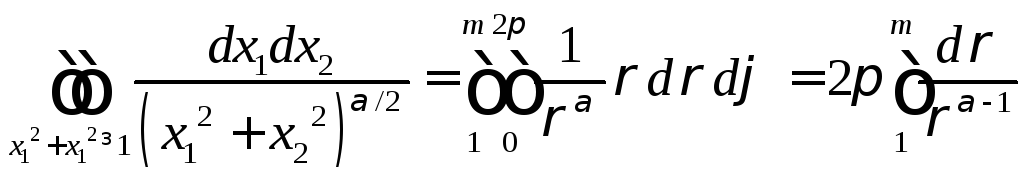 .
.
При
каких
![]() интеграл ограничен по
интеграл ограничен по![]()
![]()
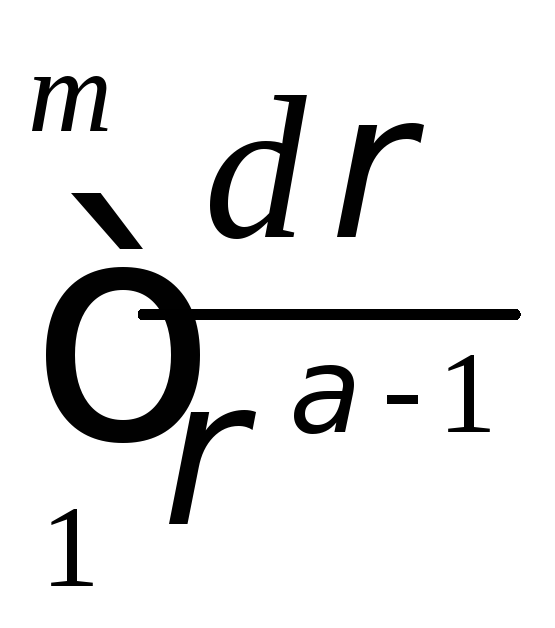 сходится
сходится![]() .
.
Для
исследования сходимости интеграла
![]() будем использовать сферическую систему
координат
будем использовать сферическую систему
координат
![]() ,
,
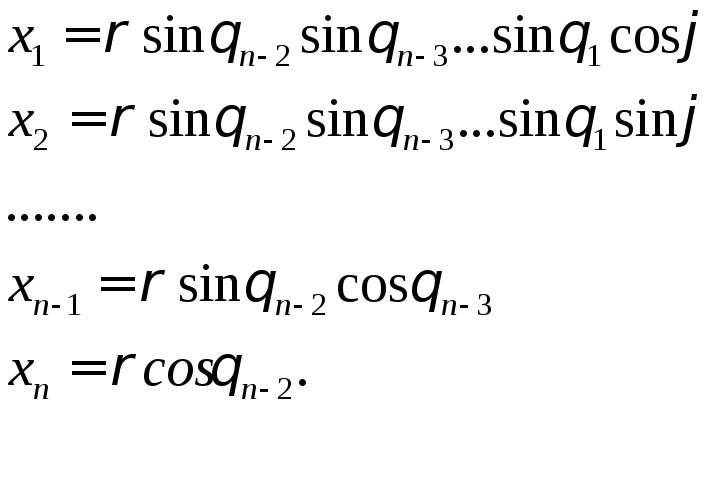
В ней
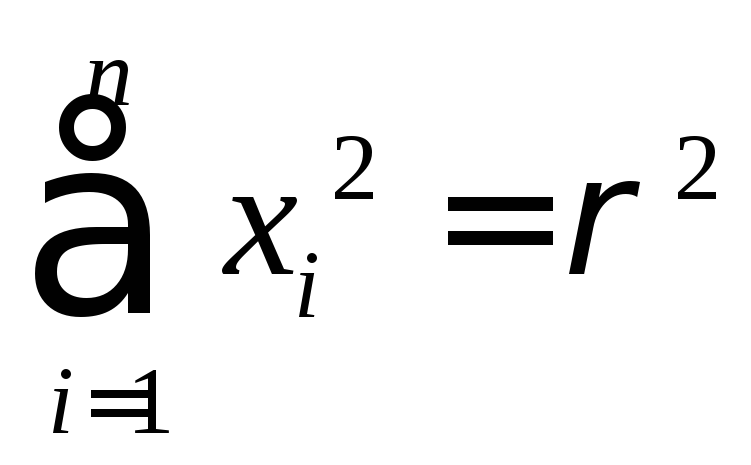 ,
,
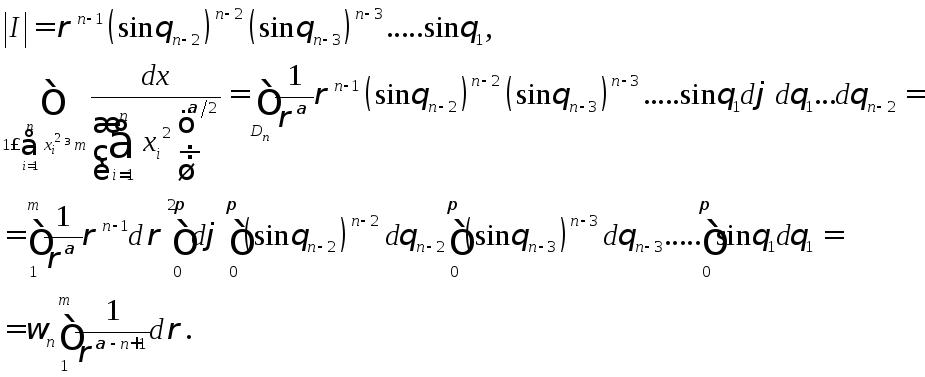
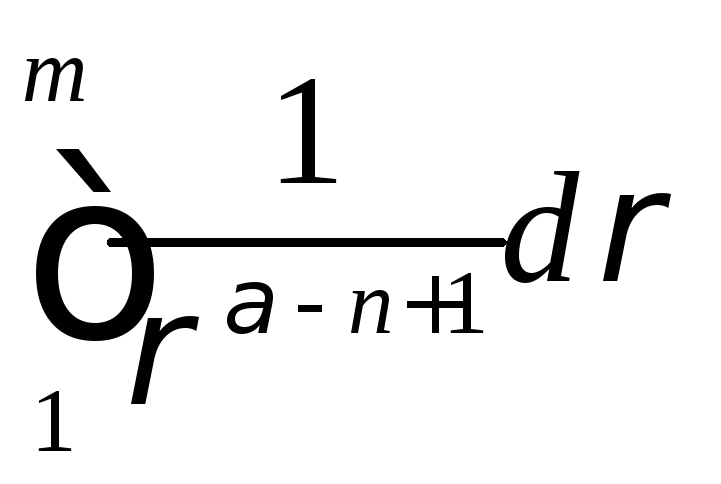 -
ограничен
-
ограничен
![]() сходится
сходится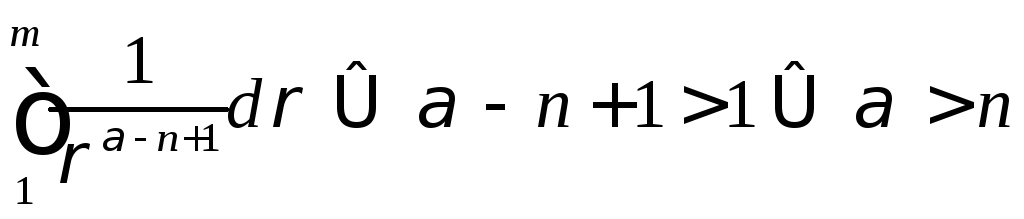 .
.
Здесь
![]() есть
площадь поверхности сферы единичного
радиуса.
есть
площадь поверхности сферы единичного
радиуса.
При
![]() ,
,![]() -
объем шара радиуса
-
объем шара радиуса![]() ,
,
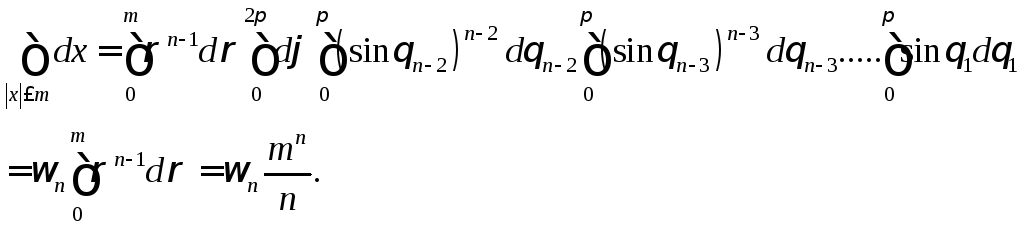
Имеем
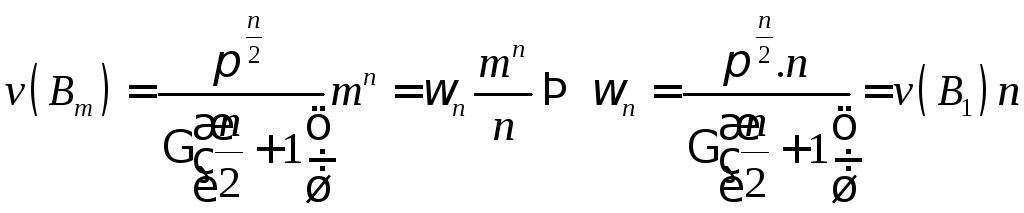 .
.
3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
Признак сравнения
Пусть
![]() -
измеримая по Жордану область,
-
измеримая по Жордану область,
![]() ,
,
![]() ,
,![]() .
.
Последовательность
множеств
![]() из
из![]() называется
называется![]() -допустимой
, если
-допустимой
, если
1.
![]() ограничены, измеримы по Жордану,
ограничены, измеримы по Жордану,
2.
![]() ,
,![]() ,
,
3.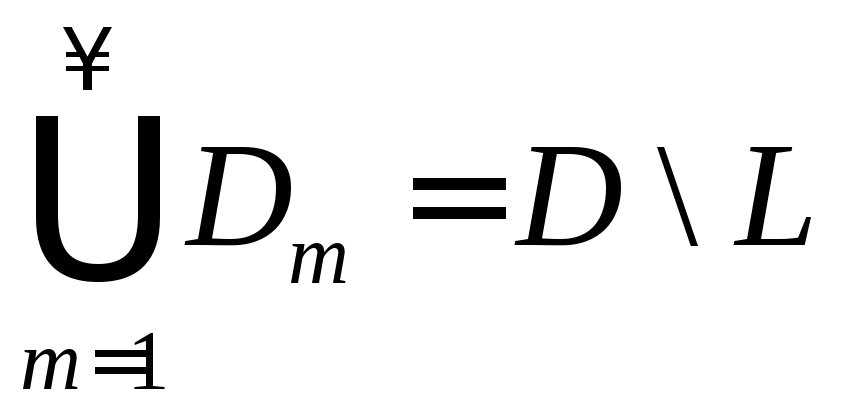 .
.
Пример
:
![]() ,
,![]() -допустимой
последовательностью будет , например,
последовательность множеств
-допустимой
последовательностью будет , например,
последовательность множеств![]() .
.
Число
![]() называется несобственным интегралом
второго рода от функции
называется несобственным интегралом
второго рода от функции![]() по ограниченной области
по ограниченной области![]() ,
если для любой последовательности
,
если для любой последовательности![]() ,
,![]() -допустимых
множеств существует
-допустимых
множеств существует![]() .
.
Если
сходится интеграл
![]() ,то говорят,
что интеграл
,то говорят,
что интеграл
![]() сходится абсолютно.
сходится абсолютно.
Теорема.
Несобственный
интеграл
![]() сходится
сходится![]()
![]() - сходится.
Интеграл
- сходится.
Интеграл
![]() сходится
сходится
![]() последовательность
последовательность![]() ограниченная хотя бы для одной
последовательности
ограниченная хотя бы для одной
последовательности![]() -допустимых
множеств.
-допустимых
множеств.
Признак сравнения можно записать в следующей форме.
Теорема.
Пусть функции
![]() интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве
интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве
![]() и
и![]() .
Тогда имеем
.
Тогда имеем
если несобственный интеграл
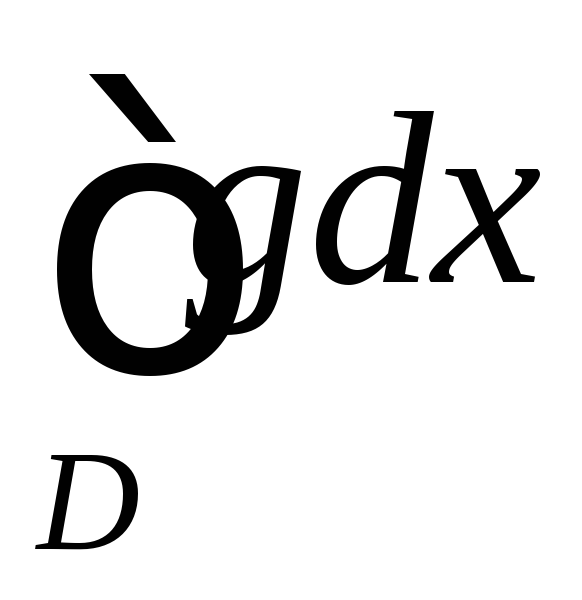 сходится, то несобственный интеграл
сходится, то несобственный интеграл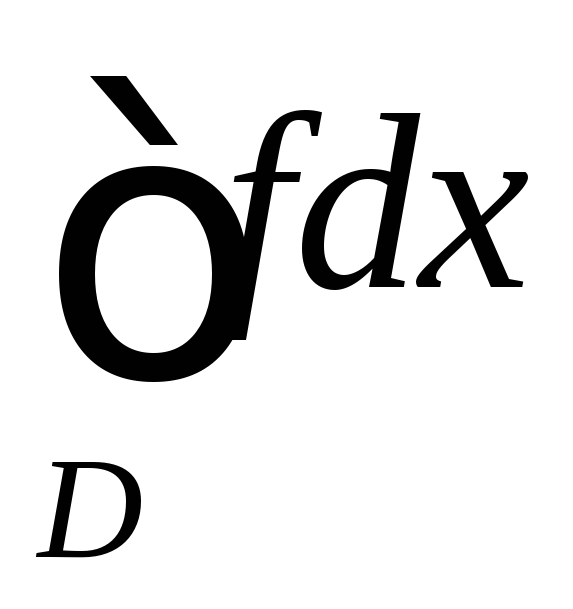 тоже сходится;
тоже сходится;если несобственный интеграл
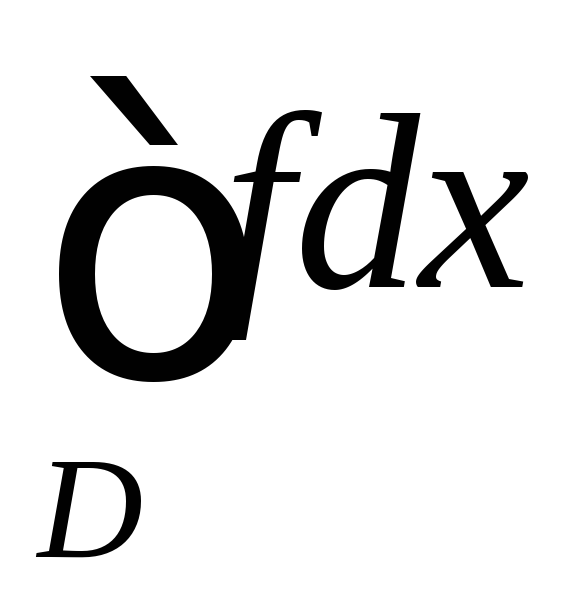 расходится, то несобственный интеграл
расходится, то несобственный интеграл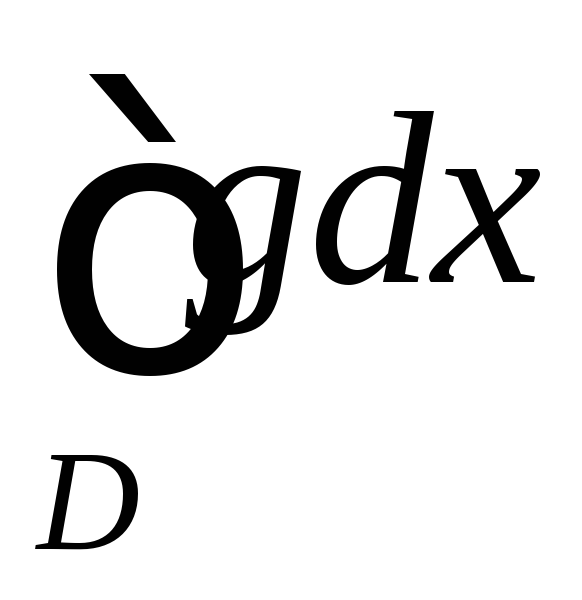 тоже расходится.
тоже расходится.
