
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
1. Ориентация на поверхности и ее границе
Вначале
рассмотрим ориентацию пространства
![]() .
В
.
В![]() имеется стандартный ортогональный
базис
имеется стандартный ортогональный
базис
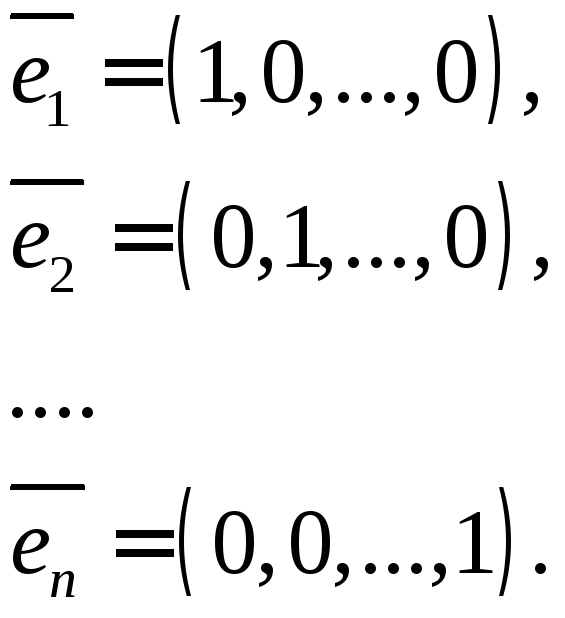
Под
ориентацией пространства
![]() понимают определенный порядок этих
базисных векторов.
понимают определенный порядок этих
базисных векторов.
Всего
существует
![]() ориентаций. Все эти ориентации можно
разбить на 2 класса. 2 ориентации попадут
в один класс, если от одной ориентации
к другой можно перейти за четное число
транспозиций. Понятно, что ориентацию
пространства можно осуществлять и на
языке координат вектора
ориентаций. Все эти ориентации можно
разбить на 2 класса. 2 ориентации попадут
в один класс, если от одной ориентации
к другой можно перейти за четное число
транспозиций. Понятно, что ориентацию
пространства можно осуществлять и на
языке координат вектора![]() .
.
![]() -мерная
поверхность
-мерная
поверхность![]() определяется при помощи отображения
определяется при помощи отображения![]() ,
,![]()
![]() Ориентация поверхности – это определенный
порядок параметров
Ориентация поверхности – это определенный
порядок параметров![]()
Граница
поверхности
![]() .
Так как граница
.
Так как граница![]() -
-![]() -мерная
поверхность в
-мерная
поверхность в![]() ,
то ее ориентацию можно задать при помощи
нормали, определяемой заданным порядком
параметров. Тогда ориентация на
,
то ее ориентацию можно задать при помощи
нормали, определяемой заданным порядком
параметров. Тогда ориентация на![]() будет определять ориентацию на
будет определять ориентацию на![]() ,
согласованную с ориентацией на
,
согласованную с ориентацией на![]() .
.
2. Интегрирование дифференциальной формы по ориентированной поверхности
Пусть
![]() -дифференциальная
форма порядка
-дифференциальная
форма порядка![]() в пространстве
в пространстве![]()
![]() ,
-
,
-
![]() -мерная
поверхность в
-мерная
поверхность в![]() ,
ориентированная порядком
,
ориентированная порядком
![]() ,
,
![]() -
сужение формы
-
сужение формы
![]() на поверхность
на поверхность![]() с учетом её ориентации.
с учетом её ориентации.
Определение.
Интегралом
от дифференциальной формы
![]() порядка
порядка![]() по поверхности
по поверхности![]() ,
ориентированной
,
ориентированной![]() ,
называется число
,
называется число
![]() ,
,
равное
![]() -кратному
интегралу от функции
-кратному
интегралу от функции![]() по области
по области![]() .
.
ЛЕКЦИЯ 26
Общая формула Стокса. Частные случаи общей формулы Стокса
1. Общая формула Стокса
Пусть
![]() ,
,![]() ,
,![]() -
-![]() -мерная
ориентированная поверхность,
-мерная
ориентированная поверхность,![]()
![]() -
дифференциальная форма порядка
-
дифференциальная форма порядка
![]() ,
,
![]() -
граница области
-
граница области
![]() ,
,![]() - граница или край поверхности
- граница или край поверхности
![]() .
Ориентация на границе
.
Ориентация на границе
![]() согласована с ориентацией на
согласована с ориентацией на![]() .
.
Теорема (Общая формула Стокса). При указанных предположениях справедливо равенство
![]() .
.
2. Частные случаи общей формулы Стокса
Рассмотрим несколько частных случаев.
1)
![]() ,
,
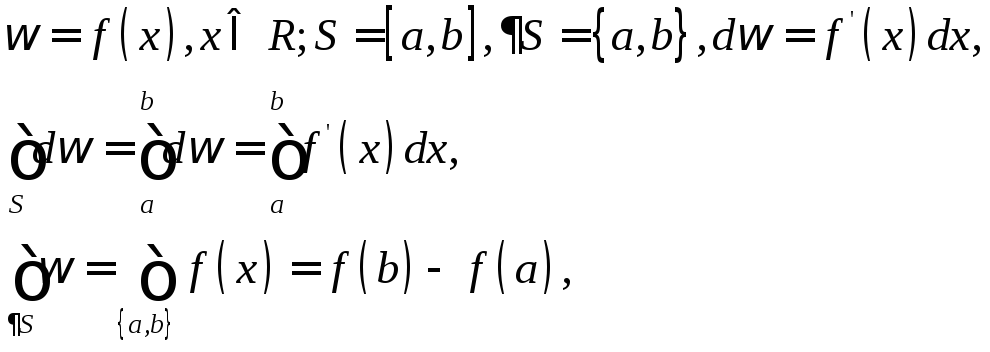
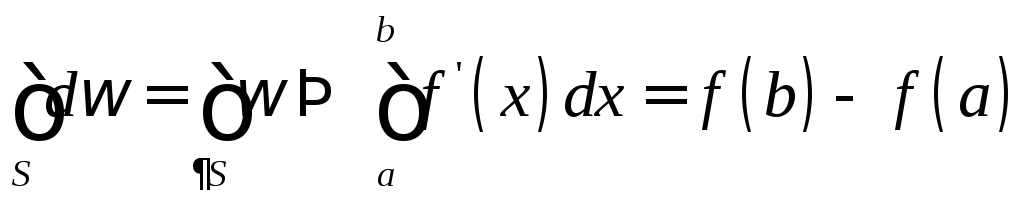 -
формула Ньютона — Лейбница.
-
формула Ньютона — Лейбница.
2)
![]() ,
,
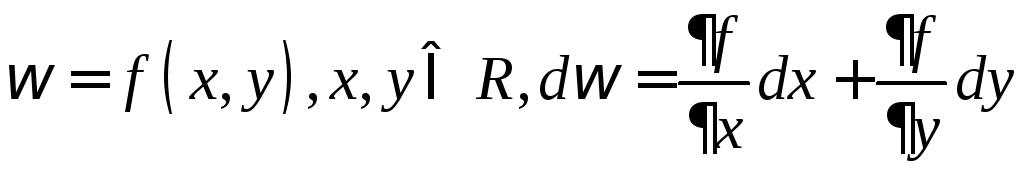 ,
,
![]() -кривая,
-кривая,![]() ,
,
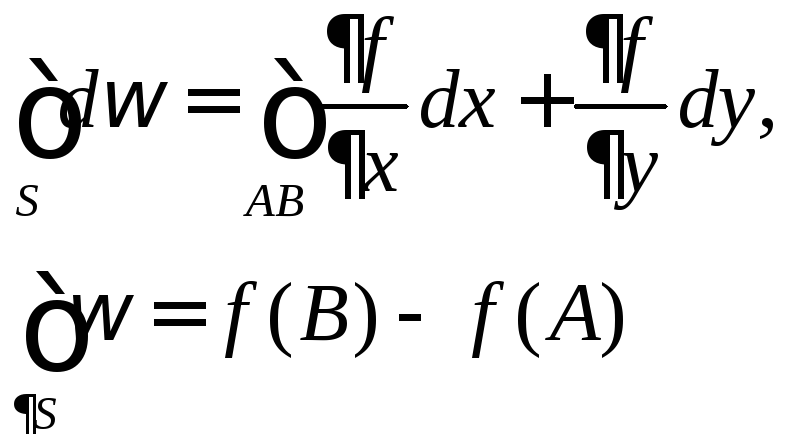
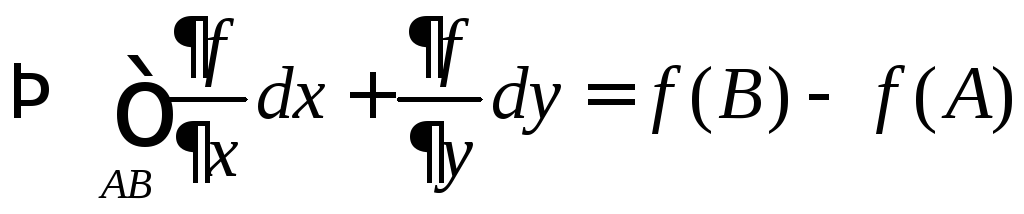 -
работа потенциального векторного поля.
-
работа потенциального векторного поля.
3)
![]() ,
,
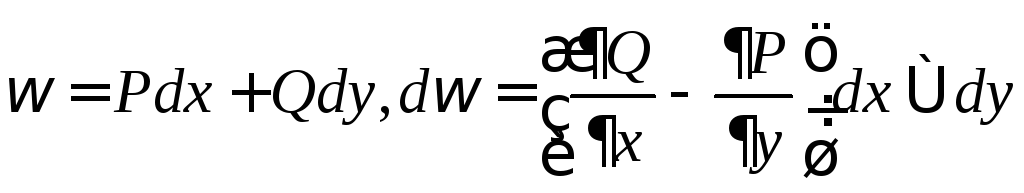 ,
,
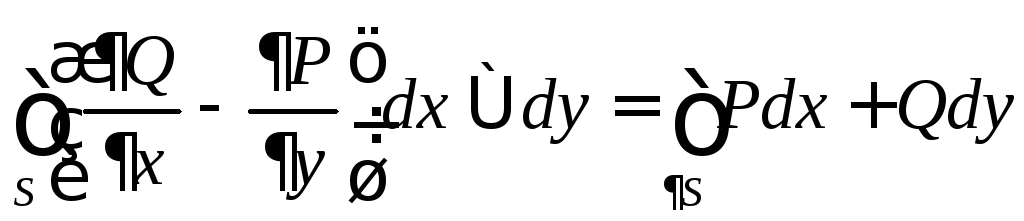 -
формула Грина.
-
формула Грина.
4)
![]() ,
,
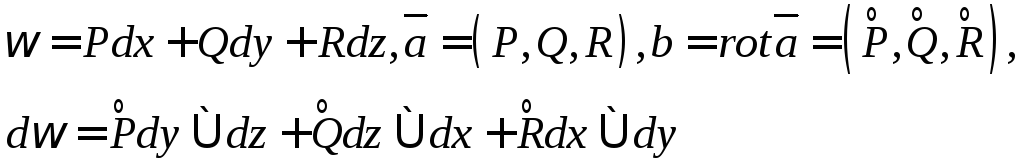
![]() -Формула
Стокса.
-Формула
Стокса.
5)
![]() ,
,
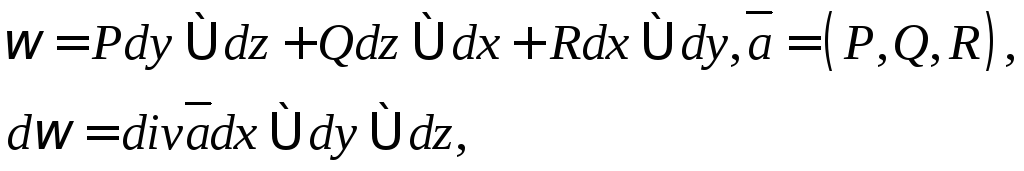
![]() ,
,
![]()
![]() -формула Гаусса
-Остроградского.
-формула Гаусса
-Остроградского.
