
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
2. Критерий Коши
Для
того чтобы функция
![]() была интегрируема на прямоугольнике
была интегрируема на прямоугольнике![]() необходимо и достаточно ,чтобы для
любого
необходимо и достаточно ,чтобы для
любого![]() существовало
существовало![]() такое, что для любых разбиений
такое, что для любых разбиений![]() и любых их разметок
и любых их разметок![]() выполняется
выполняется
![]() .
.
ЛЕКЦИЯ 2
Две леммы Дарбу. Эквивалентность двух определений интеграла Римана по прямоугольнику. Критерий Римана интегрируемости по прямоугольнику. Интегрируемость непрерывной функции
Две леммы Дарбу
Лемма
1.
![]() .
.
Лемма
2.
![]() .
.
2. Эквивалентность двух определений интеграла Римана по прямоугольнику
Теорема. Оба определения интеграла Римана является эквивалентными, т.е
Если
![]()
![]() в смысле первого определения, то
в смысле первого определения, то![]()
![]() в смысле определения второго и обратно.
в смысле определения второго и обратно.
Доказательство.
 .
Доказательство опирается на первую
лемму Дарбу.
.
Доказательство опирается на первую
лемму Дарбу.
Если
![]()
![]() и
не зависит от
и
не зависит от![]() ,
то
,
то![]() :
:![]() .
Отсюда
.
Отсюда![]() будет
будет
![]() .
Поэтому
.
Поэтому
![]()
![]() .
Переходя к пределу при
.
Переходя к пределу при![]() ,
получим
,
получим![]() ,
,![]() .
.
 .
Доказательство опирается на вторую
лемму Дарбу.
.
Доказательство опирается на вторую
лемму Дарбу.
3. Критерий Римана интегрируемости по прямоугольнику
Теорема (критерий интегрируемости Римана).
![]() ,
т.е
,
т.е
![]() интегрируема по Риману тогда и только
тогда, когда
интегрируема по Риману тогда и только
тогда, когда![]() .
.
Будем
использовать запись
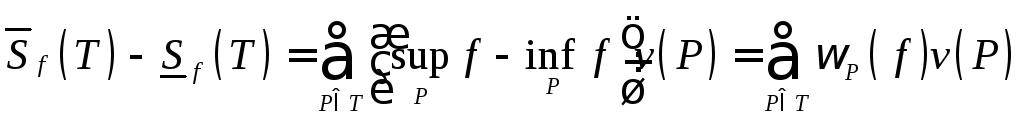 .
.
Здесь
![]() -
колебание функция на прямоугольнике
-
колебание функция на прямоугольнике![]() .
.
Следствие.
![]() является
линейным пространством и кольцом.
является
линейным пространством и кольцом.
Доказательство.
Доказательство
сводится к проверке замкнутости
![]() относительно
сложения и умножения.
относительно
сложения и умножения.
Для доказательства оценим колебания на прямоугольнике суммы и произведение функций.
а.![]() .
.
Имеем![]()
![]() .
.
Далее
![]() .
.
б.
![]()
Имеем
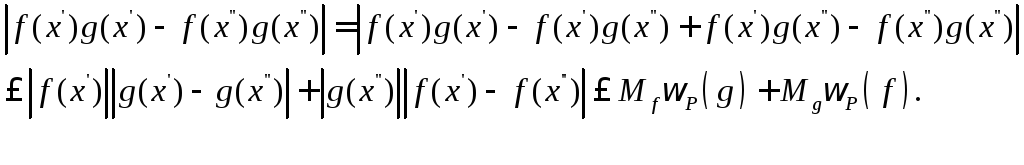
Далее все очевидно.
Интегрируемость непрерывной функции
Теорема.
![]() ,
т.е. если функция
,
т.е. если функция![]() непрерывна, то она интегрируема.
непрерывна, то она интегрируема.
Доказательство.
Имеем
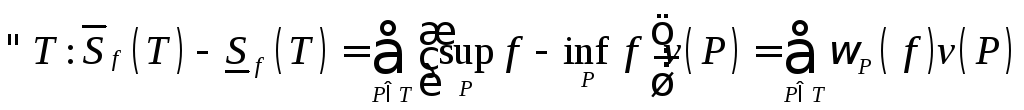 .
.
Если
![]() ,
А- компактное, то
,
А- компактное, то![]() равномерно непрерывна на А, поэтому
равномерно непрерывна на А, поэтому
![]() ,
,![]()
![]() такое, что
такое, что![]() ,
,![]() и
и![]() будет
будет![]() .
.
Итак,
![]() .
.
Отсюда,
по критерию Римана
![]() .
.
ЛЕКЦИЯ 3
Множества меры и объема нуль. Их свойства. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа. Описание множества точек разрыва
Множества меры и объема нуль. Их свойства
Определение
1. Множество
![]() имеет объем нуль
имеет объем нуль![]() или меру Жордана нуль, если для любого
или меру Жордана нуль, если для любого![]() существует конечный набор прямоугольников
существует конечный набор прямоугольников![]() ,
для которого
,
для которого
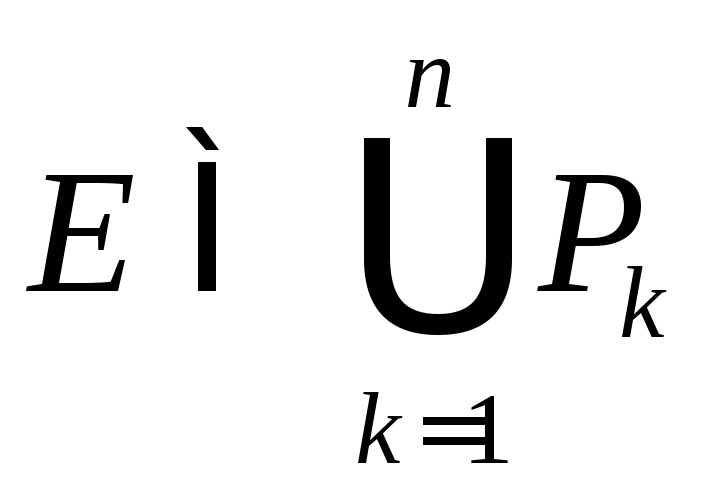 ,
,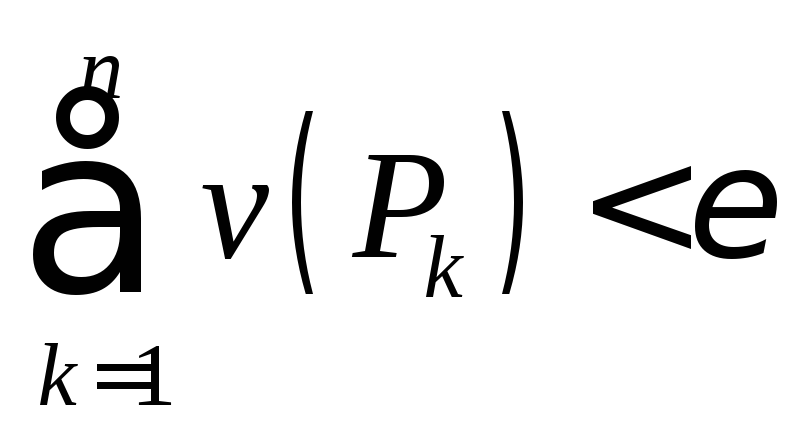 .
.
Определение
2. Множество
![]() имеет меру нуль
имеет меру нуль![]() или меру Лебега нуль, если для любого
или меру Лебега нуль, если для любого![]() существует прямоугольники
существует прямоугольники![]() ,
для которых
,
для которых
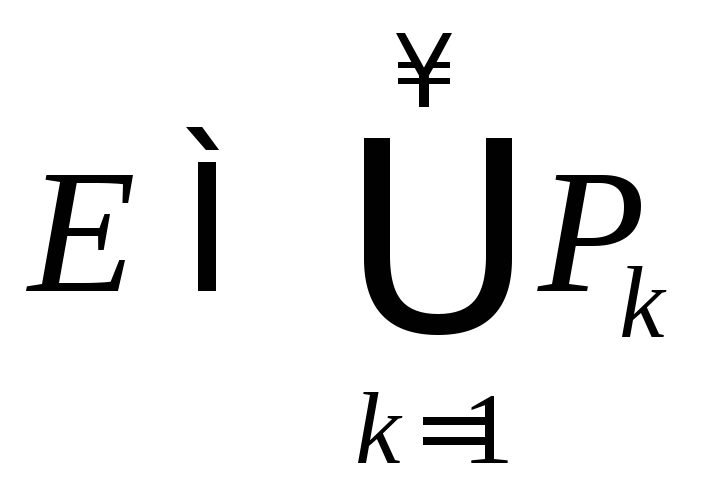 ,
,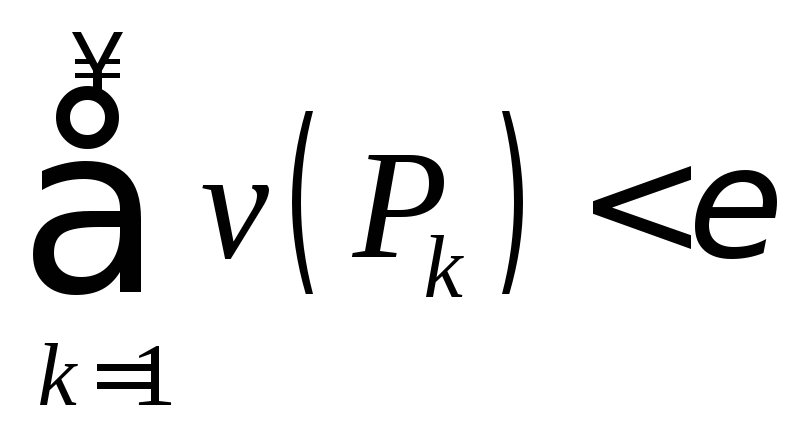 .
.
Понятно, что множество объема нуль имеет и меру нуль. Обратное утверждение не верно.
Лемма 1. Счетное объединение множеств меры нуль есть множество меры нуль.
Доказательство.
Пусть
![]() .
Тогда
.
Тогда![]() существует набор
существует набор![]() :
:
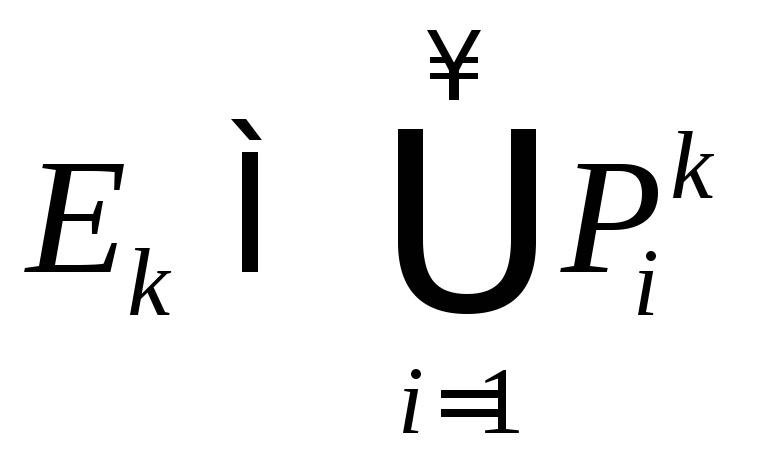 ,
,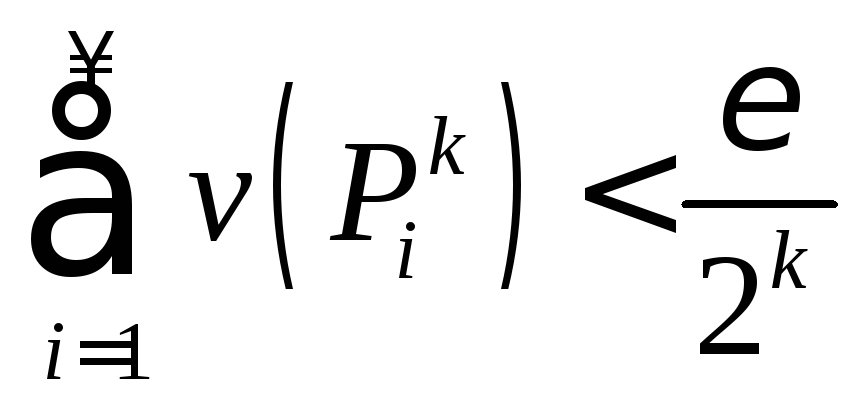 .
.
Тогда
для прямоугольников
![]() :
:
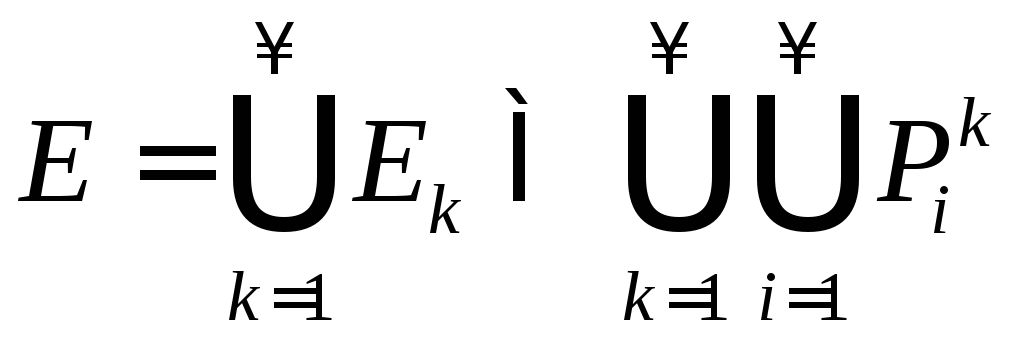 ,
,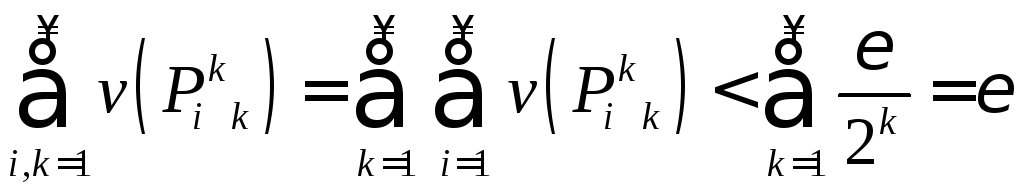 .
.
Т.е.
![]() .
.
Лемма 2. Компактное множество меры нуль имеет и объем нуль.
Доказательство.
Пусть
![]() .
Для любого
.
Для любого![]() существуют открытые прямоугольники
существуют открытые прямоугольники![]() :
:
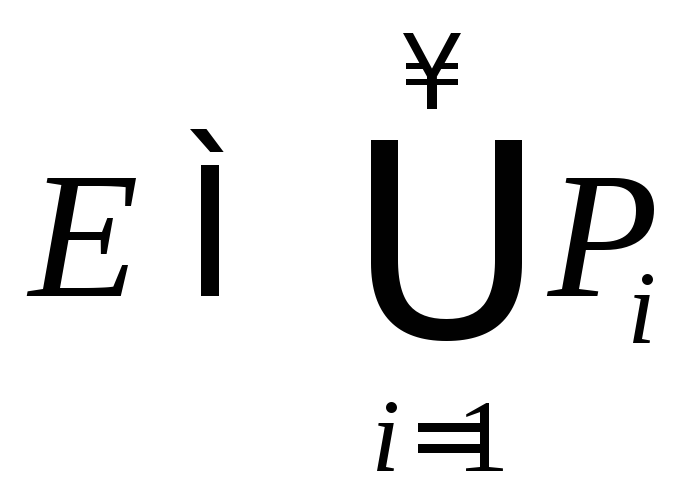 ,
,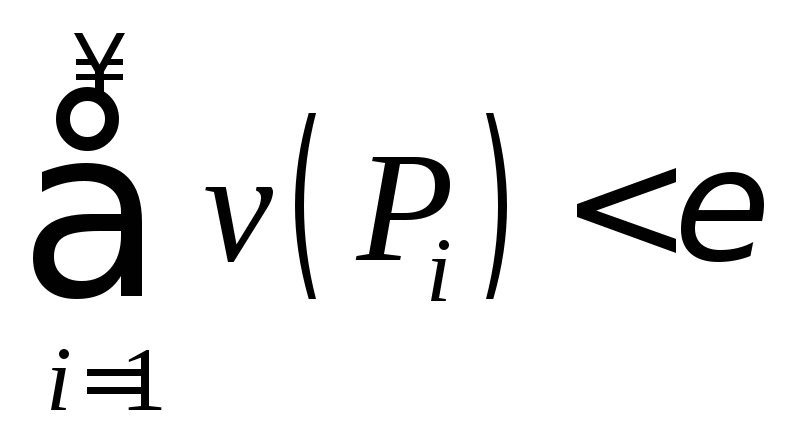 .
.
Так
как Е компактное и
![]() -
открытое покрытие Е, то по определению
компактного множества существует
конечный набор
-
открытое покрытие Е, то по определению
компактного множества существует
конечный набор![]() :
:
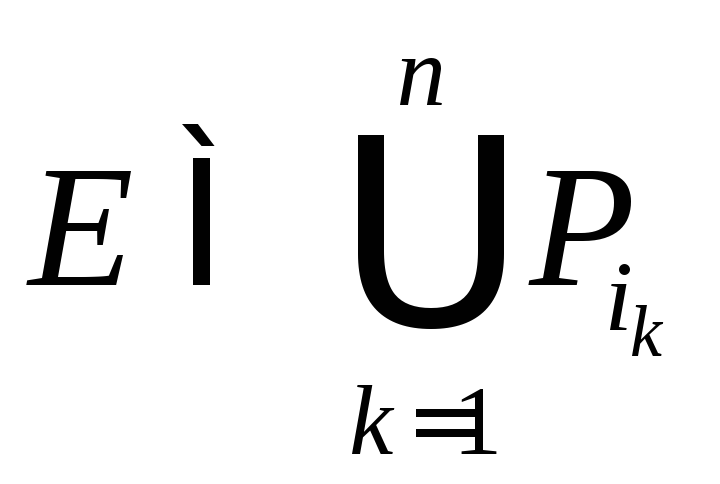 ,
,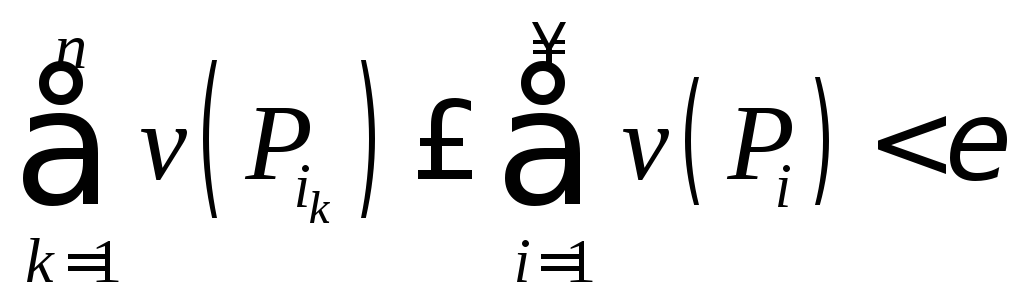 .
.
Т.е.
![]() .
.
2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
Определение
3. Колебанием
функция в точке
![]() называется число
называется число![]() .
.
Справедливы следующие утверждения.
Лемма
3.
![]() -точка
непрерывности ограниченной функции
-точка
непрерывности ограниченной функции![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
.
Доказательство.
Необходимость.
Пусть функция
![]() непрерывна в точке
непрерывна в точке![]() .
Предположим, что
.
Предположим, что![]() .
Рассмотрим
.
Рассмотрим![]() .
Из определения
.
Из определения![]() получим,
что существуют точки
получим,
что существуют точки![]() такие, что
такие, что![]() .
.
Кроме
того, имеем
![]() .
Это противоречит непрерывности функции
.
Это противоречит непрерывности функции![]() в точке
в точке![]() .
Следовательно
.
Следовательно![]() .
.
Достаточность.
Поскольку
![]() ,
то для любого
,
то для любого![]() существует
существует![]() такое, что для любых
такое, что для любых![]() имеем
имеем![]() .
Полагая
.
Полагая![]() ,
получаем непрерывность в точке
,
получаем непрерывность в точке![]() .
Лемма доказана.
.
Лемма доказана.
