
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
4. Сходимость кратных интегралов
Все аналогично случаю внешности шара:
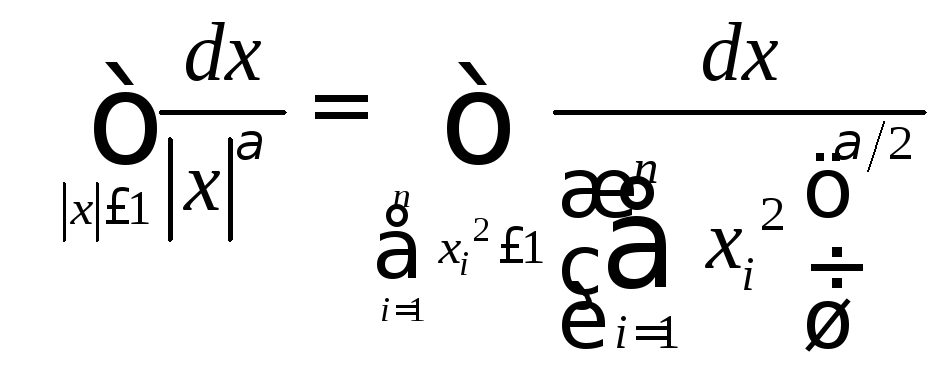 ,
,
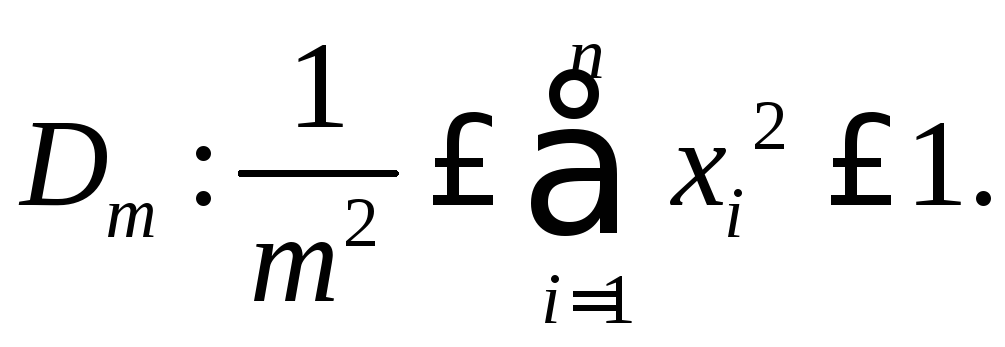
В сферической системе координат
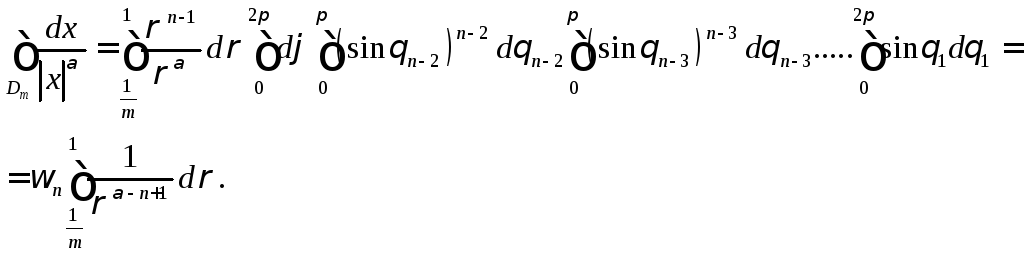
Интегралы
ограничены по
![]()
![]() интегралы
интегралы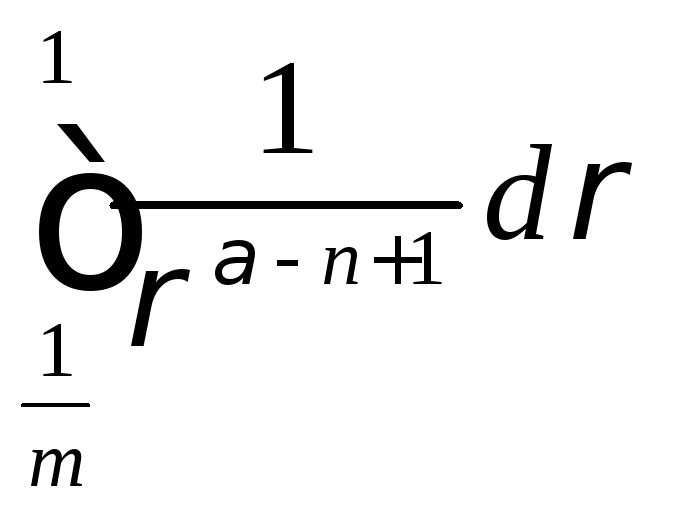 сходятся
сходятся![]()
![]() .
.
ЛЕКЦИЯ 14
Геометрические и механические приложения кратных интегралов
1. Геометрические приложения кратных интегралов
Кратный
интеграл позволяет вычислить объем
измеримого по Жордану тела![]()
2. Механические приложения двойного интеграла
Двойной интеграл позволяет вычислить массу, координаты центра тяжести, статичные моменты первого и второго порядка плоской пластинки, начиненной веществом.
Пусть
на плоскости
![]() задана плоская фигура
задана плоская фигура![]() и пусть непрерывная функция
и пусть непрерывная функция![]() - плотность распределения ее массы.
Разобьем фигуру на части
- плотность распределения ее массы.
Разобьем фигуру на части![]() сетью гладких кривых и, предполагая,
что в пределах одной части плотность
распределения масс постоянна, получаем
приближенное выражение для массы:
сетью гладких кривых и, предполагая,
что в пределах одной части плотность
распределения масс постоянна, получаем
приближенное выражение для массы:
![]() .
.
В пределе имеем
![]() .
.
Аналогично
выводятся формулы для статических
моментов первого порядка
![]() и
и![]() относительно осей
относительно осей![]() и
и![]() :
:
![]() и
и
![]() ,
,
Координаты центра тяжести пластинки вычисляются по формулам:
![]()
![]() .
.
Вторые
статические моменты (моменты инерции
относительно осей
![]() и
и![]() )
вычисляются по формулам:
)
вычисляются по формулам:
![]() и
и
![]() .
.
Наконец, момент инерции относительно начало координат имеет вид
![]() .
.
3. Механические приложения тройного интеграла
Аналогично двумерному случаю можно выписать следующие формулы.
Масса тела:
![]() .
.
Первые статические моменты относительно координатных плоскостей:
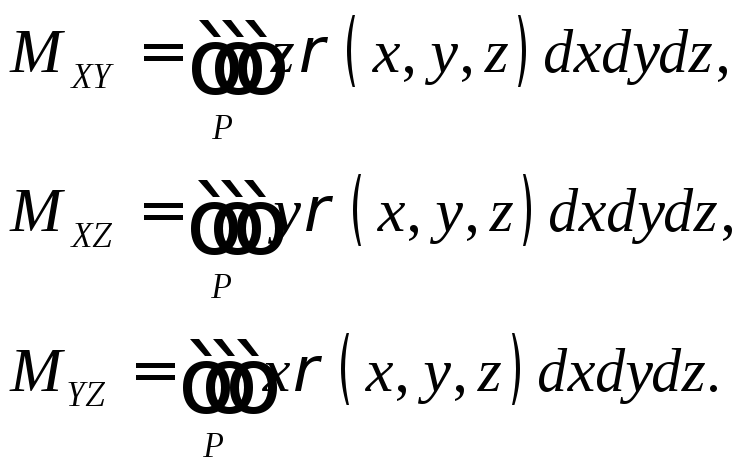
Координаты центра тяжести
![]() .
.
Вторые статические моменты:
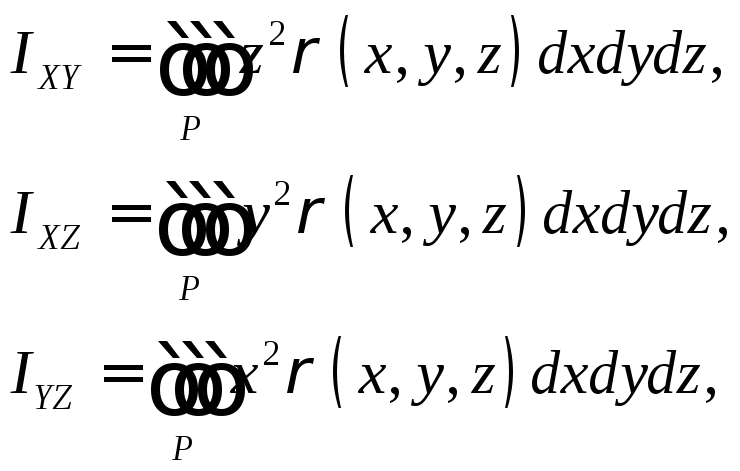
![]() .
.
ЛЕКЦИЯ 15
Криволинейный интеграл 1-го рода. Его свойства, вычисление, приложения
1. Криволинейный интеграл 1-го рода. Его свойства, вычисление
Пусть
в
![]() параметрически задана кривая
параметрически задана кривая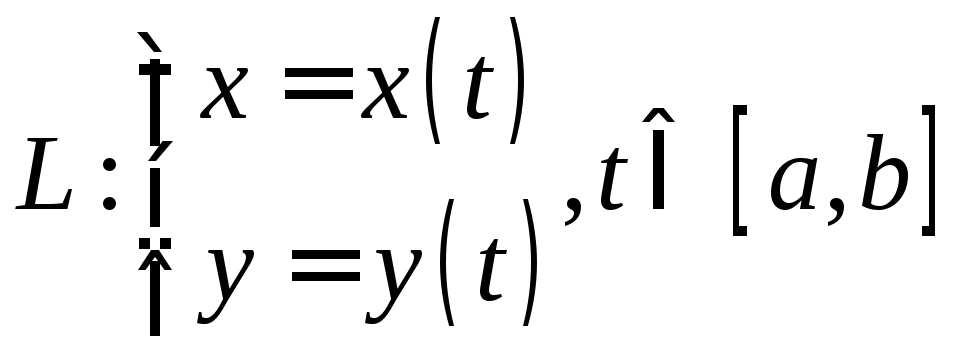
Будем
предполагать, что кривая является
гладкой( кусочно-гладкой), т.е функции
![]() непрерывно дифференцируемые:
непрерывно дифференцируемые:![]() (кусочно
непрерывно дифференцируемые). Такая
кривая является спрямляемой. В этом
случае длину дуги части кривой, отвечающей
отрезку
(кусочно
непрерывно дифференцируемые). Такая
кривая является спрямляемой. В этом
случае длину дуги части кривой, отвечающей
отрезку![]() можно вычислять при помощи формулы
можно вычислять при помощи формулы
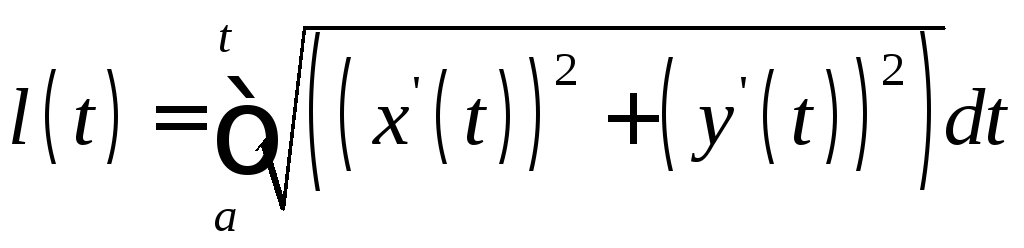 .
.
Если
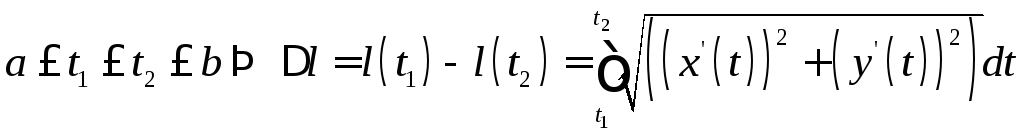 - длина части кривой, отвечающей отрезку
- длина части кривой, отвечающей отрезку![]() .
.
Пусть
![]() - разбиение отрезка
- разбиение отрезка![]() ,
,![]() -
-![]() разметка
разбиения,
разметка
разбиения,
![]() .
.
Образуем интегральную сумму
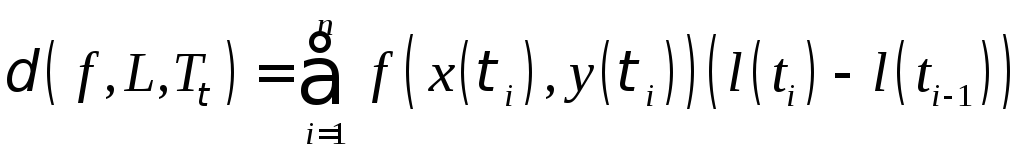 .
.
Будем
говорить, что для функции
![]() существует криволинейный интеграл
первого рода по кривой
существует криволинейный интеграл
первого рода по кривой![]() ,
если существует
,
если существует![]() ,
не зависящий от
,
не зависящий от![]() .
Т.е
.
Т.е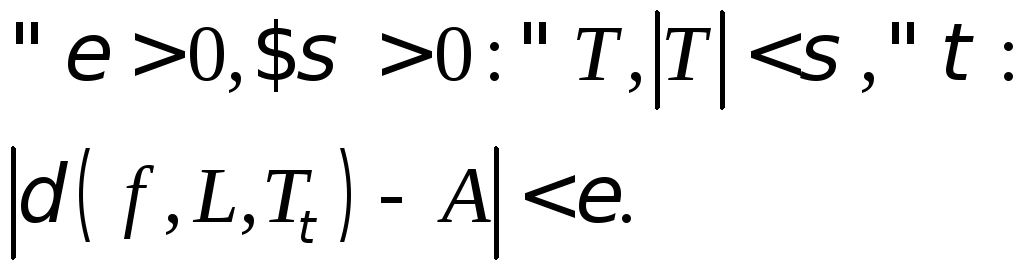
Значение интеграла полагают равным числу А:
![]() .
.
Свойства криволинейного интеграла 1-го рода:
1.
![]() .
.
2.
Если
![]() .
.
3.Если
![]() на
на![]() ,
то
,
то![]() .
.
4.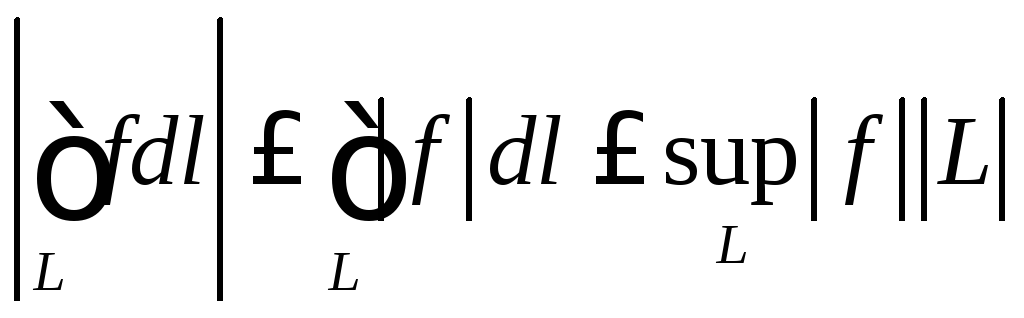 ,
,
где![]() -длина
-длина
![]()
Вычисление криволинейного интеграла 1-го рода.
По
определению интеграла сумма
![]() является интегральной суммой для
интеграла Римана-Стилтьеса
является интегральной суммой для
интеграла Римана-Стилтьеса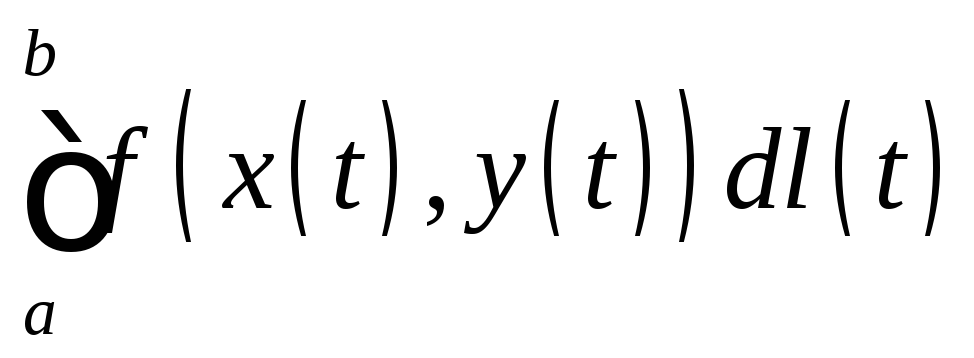 ,
поэтому
,
поэтому
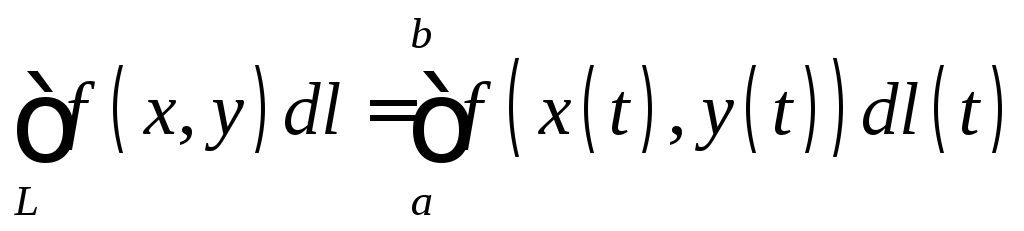 .
.
Если
![]() ,
,![]() -
гладкая кривая, то
-
гладкая кривая, то![]()
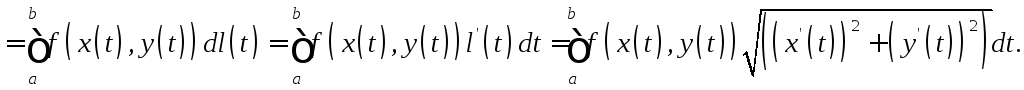
Если
кривая
![]() задана в трехмерном пространстве
задана в трехмерном пространстве
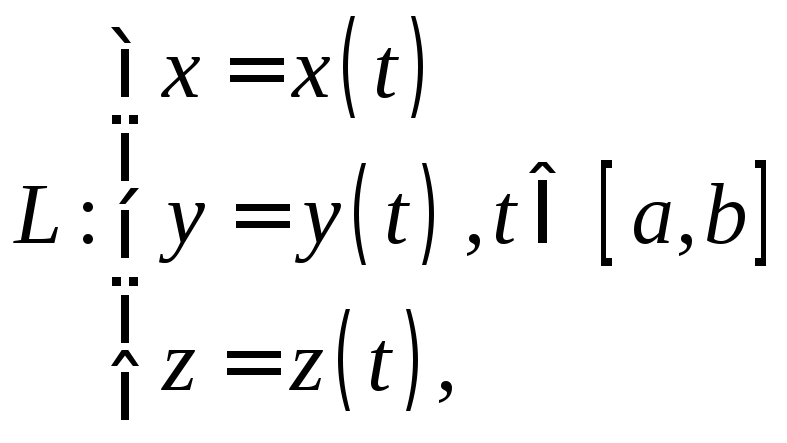
![]() ,
то аналогично
,
то аналогично
![]()
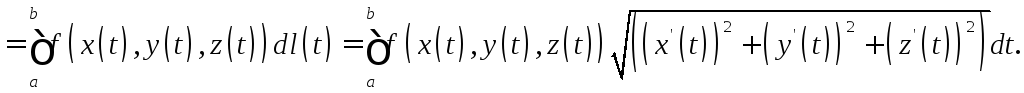
2. Приложения криволинейного интеграла 1-го рода
Геометрическое приложение: Вычисление длины кривой.
Длина
кривой
![]()
Механические приложения: Вычисление массы, статических моментов, координат центра тяжести.
Пусть
сначала
![]() -
плоская кривая
-
плоская кривая![]() - плотность на кривой
- плотность на кривой![]() .
Имеют место следующие формулы:
.
Имеют место следующие формулы:
Масса
![]() .
.
Первые
статические моменты относительно осей
![]() и
и![]()
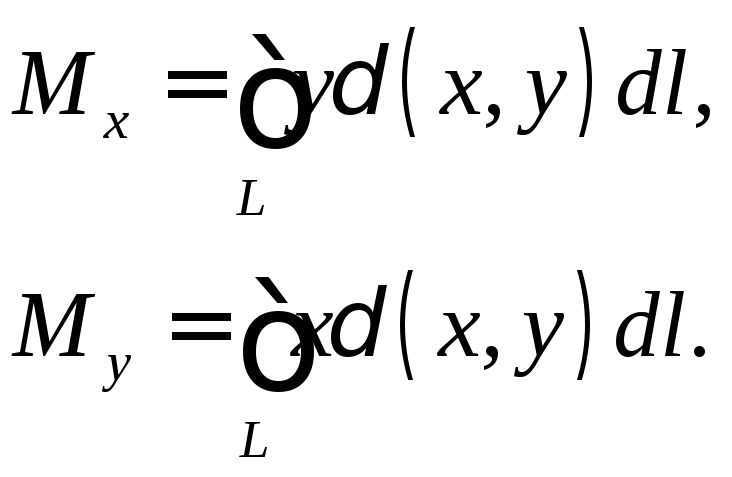
Координаты центра тяжести
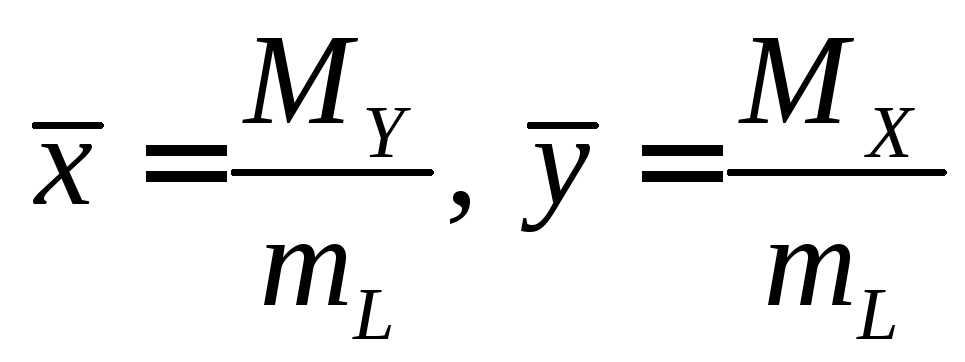 .
.
Вторые
статические моменты (моменты инерции)
относительно осей
![]() и
и![]()
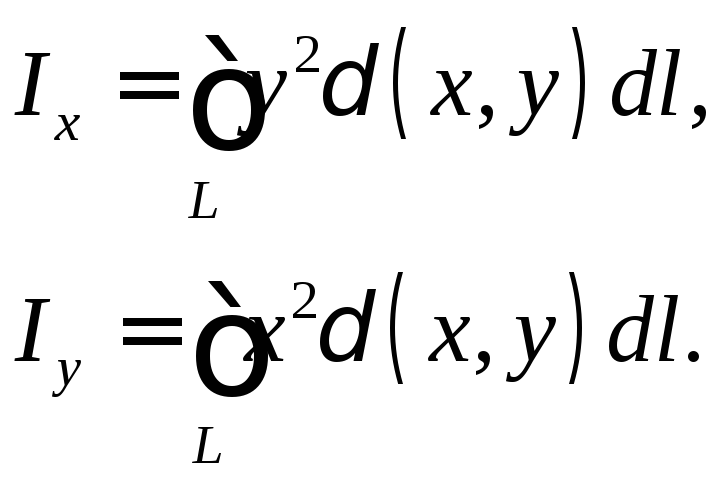
Момент инерции относительно начала координат
![]() .
.
Пусть
теперь
![]() -
пространственная кривая ,
-
пространственная кривая ,![]() -плотность на кривой
-плотность на кривой![]() .
Имеют место следующие формулы :
.
Имеют место следующие формулы :
Масса
![]() .
.
Первые статические моменты относительно координатных плоскостей
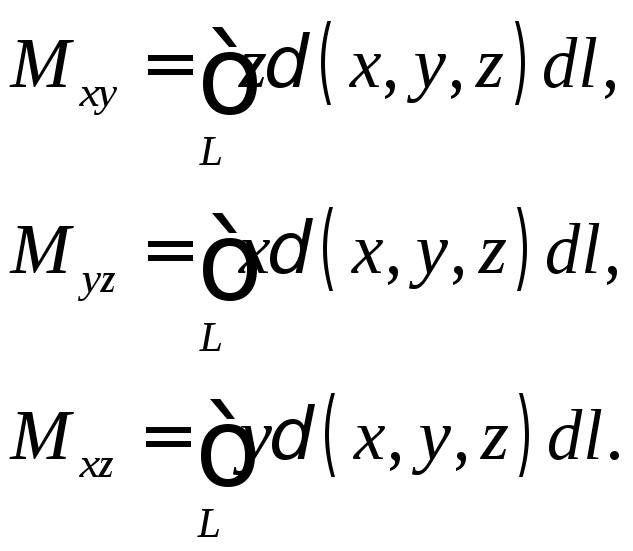
Координаты центра тяжести
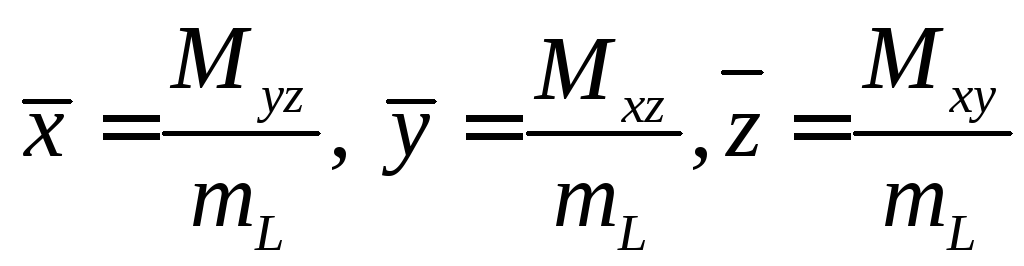 .
.
Вторые статические моменты (моменты инерции) относительно координатных плоскостей:
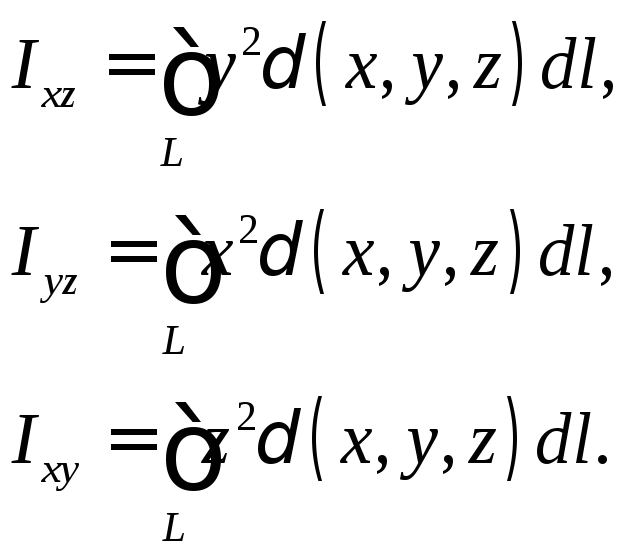
Момент инерции относительно начала координат
![]()
