Математика для инженеров

42. На плоскости даны точки А(0; –2), В(4; 2) и С(4; –2). В начале

i и j координатных осей.

43. В прямоугольнике ОАСВ (рис. 1) М и N — середины сторон ВС = 3 и АС = 4. Разложить геометрически и аналитически вектор OC c по векторам OM a и ON b .

Указание. В условие c ma nb подставить выражения a , b и c через i и j и сравнить коэффициенты слева и справа при i и j .

44.Вектор составляет с осями Ох и Oz углы 40» и 80». Найти его угол с осью Оу.

45.Радиус-вектор точки М составляет с осью Ох угол 45» и с осью Оу угол 60». Длина его r = 6. Определить координаты точки М, если ее

координата z отрицательна, и выразить вектор OM r через орты

i , j, k .

46.Даны точки А(1; 2; 3) и В(3; –4; 6). Построить вектор AB u , его проекции на оси координат и определить длину и направление вектора. Построить углы вектора u с осями координат.

47.В точке А(2; 1; –1) приложена сила R = 7. Зная две координаты этой силы Х = 2 и Y = –3, определить направление и конец вектора, изображающего силу.

48.На плоскости Оxу даны точки А(4; 2), В(2; 3) и С(0; 5) и

С(–3; 0). В начале координат приложены силы OA, OB и OC . построить

равнодействующую OM , найти ее проекции на оси координат и величину. Выразить силы OA, OB, OC и OM через единичные векторы i и j координатных осей.

51. В трапеции ОАСВ имеем ВС = ОА/3 и ВС||ОА. Разложить геометрически и аналитически вектор OA = a по векторам OC = c и

OB = b .

Указание. Из треугольника ОВС можно c выразить через b и a и затем решить полученное уравнение относительно a .

углы. Определить эти углы и построить вектор r , если его длина равна 2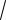3 .

54. Вектор составляет с осями Оу и Оz углы 60» и 120». Какой угол

геометрически и аналитически вектор c по векторам a и b .

¬5. Скалярное произведение векторов

58.На плоскости дан треугольник с вершинами О(0; 0), А(2a; 0) и В(a; –a). Найти угол, образованный стороной ОВ и медианой ОМ этого треугольника.

59.Из вершины квадрата проведены прямые, делящие противоположные стороны пополам. Найти угол между ними.

угол (a, b ) 135».

62. Определить длины диагоналей параллелограмма, построенного на векторах a 2m n и b m 2n , где m и n – единичные векторы, угол между которыми 60».

треугольника, величину угла А и направляющие косинусы биссектрисы угла А.

угол (a, b ) 60 ». Определить угол между медианой OM треугольника

АОВ и стороной OA .

67. Из вершины прямоугольника со сторонами 6см и 4см проведены прямые, делящие противоположные стороны пополам.

сторон ВС = 2 и АС = 2. Острый угол трапеции 60». Определить угол

между векторами OM и ON .

71. Проекции перемещения движущейся точки на оси координат sx = 2, sy = 1, sz = –2м. Проекции действующей силы F на оси координат равны Fx = 5H, Fy = 4H, и Fz = 3H. Вычислить работу А силы F (A = F s ) и угол между силой F и перемещением s .

¬6. Векторное и смешанное произведения векторов

72. Векторы a и b образуют угол . Зная, что a 6, b 5, 6

вычислить a b .

73. Даны a 10, b 2 и ab 12 . Вычислить a b .

74. Даны векторы a 3; 1; 2 и b 1;2; 1 . Найти координаты векторных произведений: 1) a b , 2) (2a b ) b , 3) (2a b ) (2a b ) .

величину и направляющие косинусы момента этой силы относительно начала координат.

80. Вычислить объем тетраэдра, вершины которого находятся в

83.Даны точки A(2; 1; 2), B(1; 2; 1) и C(3; 2; 1). Найти координаты векторных произведений: 1) AB BC ; 2) BC 2CA CB .

84.Дан треугольник с вершинами A(1; 2; 8), B(0; 0; 4) и C(6; 2; 0). Вычислить его площадь и высоту BD.

85.Сила P 2; 4;5 приложена к точке M0(4; 2; 3). Определить

момент этой силы относительно точки A(3; 2; 1).

86. Сила f 2;2;9 приложена к точке A(4; 2; 3). Определить величину и направляющие косинусы момента этой силы относительно

1 Если вектор F изображает силу, приложенную к какой-нибудь точке М, а вектор a , идет из некоторой точки О в точку M, то вектор a F представляет собой момент силы F относительно точки О.

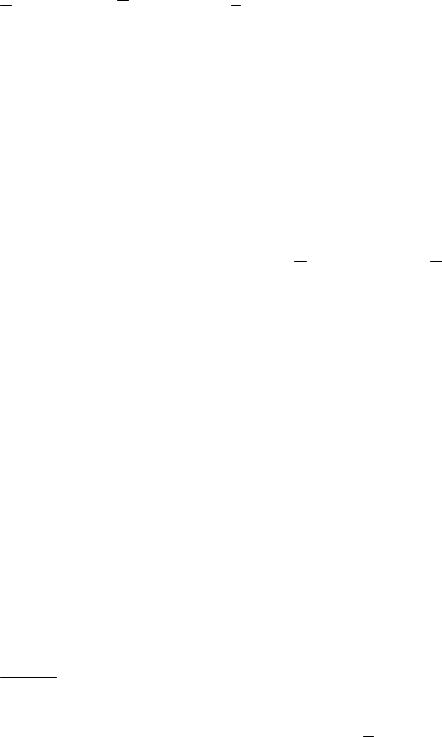
3) a 2; 1;2 b 1;2; 3 c 3; 4;7 .

89. Даны вершины тетраэдра: A(2; 3; 1), B(4; 1; 2), C(6; 3; 7), D( 5; 4; 8). Найти длину его высоты, опущенной из вершины D.

¬7. Плоскость и прямая в пространстве

90.Точка Р(2; 1; 1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.

91.Составить уравнение плоскости, проходящей через точку

М1(3; 4; 5) параллельно двум векторам a1 3;1; 1 и a 2 1; 2;1 .

92.Составить уравнение плоскости, проходящей через три точки M1(3; 1; 2), M2(4; 1; 1), и M3(2; 0; 2).

93.Составить уравнение плоскости, которая проходит через

начало координат параллельно плоскости 5x 3y + 2z 3 = 0.

94. Составить уравнение плоскости, которая проходит через точку M1(2; 1; 1) перпендикулярно к двум плоскостям: 2x z + 1 = 0, y = 0.

95. Две грани куба лежат на плоскостях 2x 2y + z 1 = 0, 2x 2y + z + 5 = 0. Вычислить объем этого куба.

96. Составить канонические уравнения прямой, проходящей через

3x y 2z 7 0, точку M1(2; 3; 5) параллельно прямой

x 3y 2z 3 0.

97.Составить уравнения прямой, проходящей через точку M0(2; 3; 5) перпендикулярно к плоскости 6x 3y 5z + 2 = 0.

98.Даны две точки M1(3; 1; 2) и M2(4; 2; 1). Составить уравнение плоскости, проходящей через точку M1 перпендикулярно

вектору M1M 2 .

99.Составить уравнение плоскости, проходящей через точки M1(2; 1; 3) и M2(3; 1; 2) параллельно вектору a 3; 1;4 .

100.Составить уравнение плоскости, которая проходит через точку M1(3; 2; 7) параллельно плоскости 2x 3z + 5 = 0.

101.Составить уравнение плоскости, которая проходит через две

точки M1(1; 1; 2) и M2(3; 1; 1) перпендикулярно к плоскости x 2y + 3z 5 = 0.

¬8. Смешанные задачи на прямую и плоскость

107. Составить уравнение плоскости, проходящей через прямую

2x y z 3 0, x = 3t + 1, y = 2t + 3, z = t 2 параллельно прямой

x 2 y z 5 0.

108.Составить уравнение плоскости, проходящей через прямую x = 2t + 1, y = 3t + 2, z = 2t 3 и точку M1(2; 2; 1).

109.Составить уравнение плоскости, проходящей через точку

M1(1; 2; 3) параллельно прямым:

x 1 y 1 z 7 , x 5 y 2 z 3 .

y = 5t 7, z = 2t + 2.

115.Составить уравнение плоскости, проходящей через прямую x 1 y 2 z 2 перпендикулярно к плоскости 3x + 2y z 5 = 0.

M2(3; 2; 2).

119.Составить уравнения прямой, образованной пересечением плоскости 3x y 7z + 9 = 0, с плоскостью, проходящей через ось Ox и точку E(3; 2; 5).

120.Через точки M1( 6; 6; 5) и M2(12; 6; 1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.

121. Вычислить объем пирамиды, ограниченной плоскостью 2x 3y + 6z 12 = 0 и координатными плоскостями.

122. Найти точку Q, симметричную точке P(2; 5; 7) относительно прямой, проходящей через точки M1(5; 4; 6) и M2( 2; 17; 8).

¬9. Уравнение прямой на плоскости

123.Написать уравнение прямой, проходящей через точку А(4; 3)

иотсекающей от координатного угла треугольник площадью 3 кв. ед.

124.Равнобедренная трапеция с основаниями 8см и 2см имеет острый угол 45». Написать уравнения сторон трапеции, приняв за ось Ох большее основание и за ось Оу — ось симметрии трапеции.

125.В треугольнике с вершинами А(–2; 0), В(2; 6) и С(4; 2) проведены высота BD и медиана ВЕ. Написать уравнения стороны АС, медианы ВЕ и высоты BD.

126.Найти длину высоты BD в треугольнике с вершинами А(–3; 0), В(2; 5) и С(3; 2).

127.Определить вершины и углы треугольника, стороны которого заданы уравнениями х + 3у = 0, х = 3, х – 2у + 3 = 0.

128.Написать уравнения сторон ромба с диагоналями 10см и 6см, приняв большую диагональ за ось и меньшую — за ось Оу.

129.Написать уравнение прямой, проходящей через точку (–4; 6) и отсекающей от осей координат треугольник площадью 6.

130.Дан треугольник с вершинами А(–2; 0), В(2; 4) и С(4; 0). Написать уравнения сторон треугольника, медианы АЕ, высоты АD и найти длину медианы АЕ.

131.Написать уравнения сторон и найти углы треугольника с вершинами А(0; 7), В(6; –1) и С(2; 1).

132.Проверить, что точки А(–4; –3), В(–5; 0), С(5; 6) и D(1; 0) служат вершинами трапеции, и найти ее высоту.

¬10. Смешанные задачи на прямую на плоскости

133.Даны точки А(–4; 0) и В(0; 6). Через середину отрезка АВ провести прямую, отсекающую на оси Ох отрезок, вдвое больший, чем на оси Оу.

134.Даны точки А(–2; 0) и В(2; –2). На отрезке ОА построен параллелограмм OACD, диагонали которого пересекаются в точке В. Написать уравнения сторон, диагоналей параллелограмма и найти угол CAD.

135.Даны уравнения боковых сторон равнобедренного треугольника 3х + у = 0 и х – 3у = 0 и точка (5; 0) на его основании. Найти периметр и площадь треугольника.

расположены на одинаковой высоте; расстояние между ними равно 20м. Величина его прогиба на расстоянии 2м. от точки крепления, считая по горизонтали, равна 14,4см. Определить величину прогиба этого троса в середине между точками крепления, приближенно считая, что трос имеет форму дуги параболы.

150. Дан эллипс 9x2 + 5y2 = 45. Найти: его полуоси; фокусы; эксцентриситет; уравнения директрис.

151. Составить уравнение эллипса, фокусы которого лежат на оси ординат, симметрично относительно начала координат, зная, что

расстояние между его фокусами 2с = 6 и эксцентриситет e 3 . 5

152. Построить гиперболу x2 – 4y2 = 16, ее асимптоты и директрисы. Найти фокусы и эксцентриситет гиперболы.

153. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, зная, что

уравнения асимптот y 4 x и расстояние между фокусами 2с = 20. 3

154.Написать каноническое уравнение гиперболы, зная, что расстояния от одной из ее вершин до фокусов равны 9 и 1.

155.Фокусы гиперболы совпадают с фокусами эллипса x2 y 2 1. Составить уравнение гиперболы, если ее эксцентриситет

259

е= 2.

156.Зеркальная поверхность прожектора образована вращением параболы вокруг ее оси симметрии. Диаметр зеркала 80см., а глубина его 10см. На каком расстоянии от вершины параболы нужно поместить источник света, если для отражения лучей параллельным пучком он должен быть в фокусе параболы?