
- •Модуль 4. Линейные операторы. Квадратичные формы Глава 4.1. Линейные операторы §4.1.1. Линейные операторы в линейном пространстве
- •Упражнения
- •§4.1.2. Ядро и образ линейного оператора
- •Упражнения
- •§4.1.3. Матрица линейного оператора
- •Упражнения
- •§4.1.4. Сумма и произведение линейных операторов
- •Упражнения
- •§4.1.5. Собственные векторы и собственные значения
- •Упражнения
- •§4.1.6. Самосопряженный линейный оператор
- •Упражнения
- •§4.1.7. Группа ортогональных матриц
- •Упражнения
- •§4.1.8. Ортогональный линейный оператор
- •Упражнения
- •Глава 4.2. Квадратичные формы
- •§4.2.1. Матричная запись квадратичной формы
- •Упражнения
- •§4.2.2. Теорема Лагранжа
- •Упражнения
- •§4.2.3. Закон инерции
- •Упражнения
- •§4.2.4. Положительно определенные квадратичные формы
- •Упражнения
- •§4.2.5. Приведение квадратичной формы к главным осям
- •§4.2.6. Билинейная форма
- •Упражнения
- •§4.2.7. Применение квадратичных форм к исследованию линий и поверхностей второго порядка
- •Упражнения
- •Глава 4.3. Каноническая форма Жордана
- •§4.3.1. Относительная линейная независимость
- •§4.3.2. Относительный базис
- •§4.3.3. Корневые векторы
- •Упражнения
- •§4.3.4. Корневое подпространство
- •Упражнения
- •§4.3.5. Канонический базис
- •§4.3.6. Циклическое подпространство
- •§4.3.7. Построение канонического базиса в корневом подпространстве
- •§4.3.8. Построение канонического базиса в общем случае
- •§4.3.9. Единственность канонической формы Жордана
Упражнения
Линейный оператор Аунитарного (комплексного евклидового) пространства называетсянормальным, если
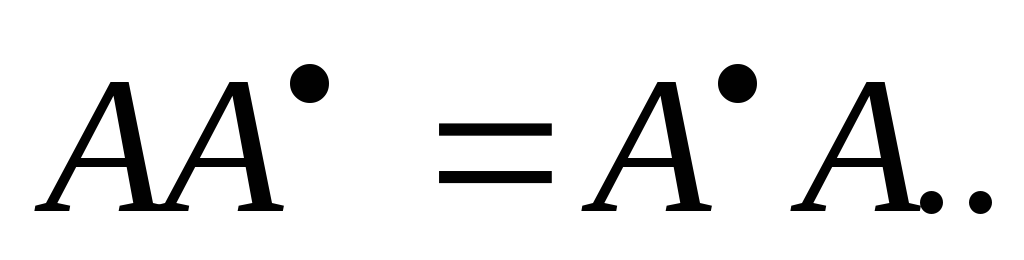 Докажите, что линейный оператор нормален
тогда и только тогда, когда для него
существует ортонормированный базис
из собственных векторов.
Докажите, что линейный оператор нормален
тогда и только тогда, когда для него
существует ортонормированный базис
из собственных векторов.Линейный оператор Uунитарного пространства называетсяунитарным, если
 Докажите, что нормальный оператор
унитарен тогда и только тогда, когда
все его собственные значения по модулю
равны единице.
Докажите, что нормальный оператор
унитарен тогда и только тогда, когда
все его собственные значения по модулю
равны единице.Линейный оператор Нунитарного пространства называетсяэрмитовым, если
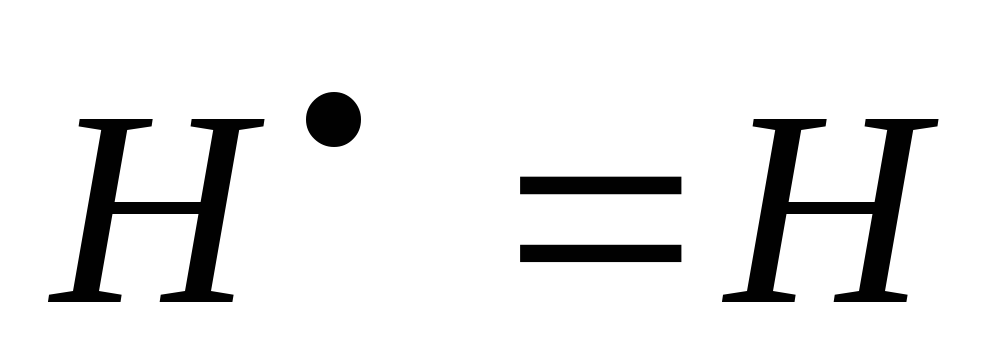 .
Линейный операторKунитарного пространства называетсякосоэрмитовым, если
.
Линейный операторKунитарного пространства называетсякосоэрмитовым, если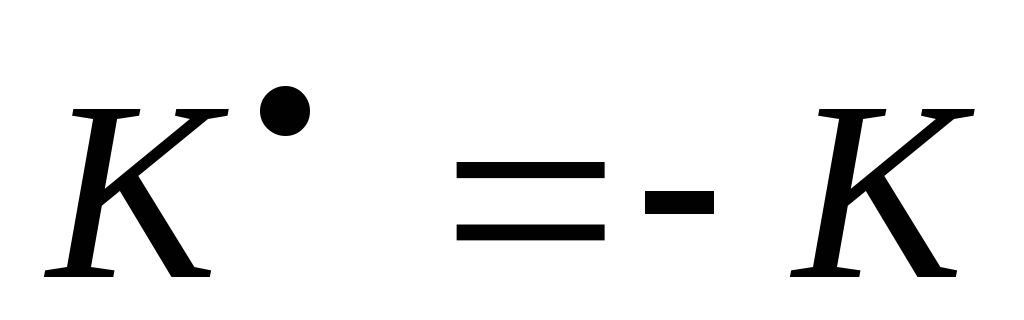 .
Докажите, что нормальный оператор
эрмитов тогда и только тогда, когда все
его собственные значения действительны.
.
Докажите, что нормальный оператор
эрмитов тогда и только тогда, когда все
его собственные значения действительны.Эрмитов оператор Hунитарного пространства называетсянеотрицательным, если
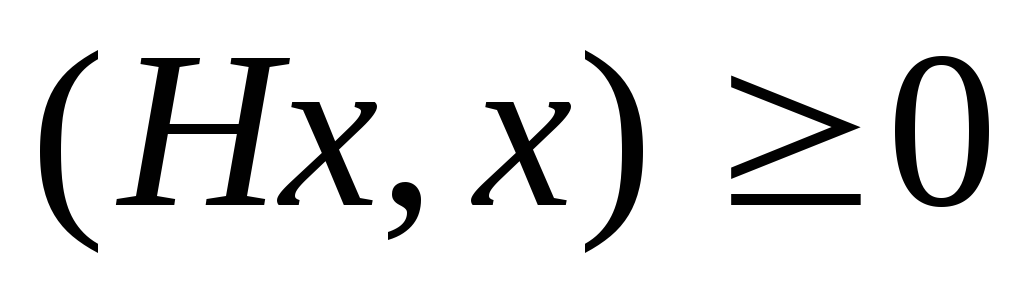 для любого ненулевого векторах.
Докажите, что эрмитов оператор
неотрицательный тогда и только, когда
все собственные значения этого оператора
неотрицательны.
для любого ненулевого векторах.
Докажите, что эрмитов оператор
неотрицательный тогда и только, когда
все собственные значения этого оператора
неотрицательны.Эрмитов оператор Hунитарного пространства называетсяположительно определенным, если
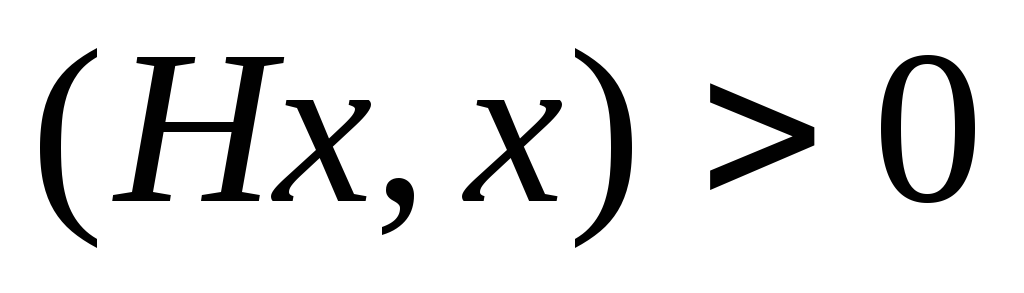 для любого ненулевого векторах.Докажите, что эрмитов оператор
положительно определен тогда и только,
когда все собственные значения этого
оператора положительны.
для любого ненулевого векторах.Докажите, что эрмитов оператор
положительно определен тогда и только,
когда все собственные значения этого
оператора положительны.Докажите, что для любого линейного оператора, действующего в унитарном пространстве, существует эрмитово разложение
![]() ,
гдеН1иН2–
эрмитовы операторы,
,
гдеН1иН2–
эрмитовы операторы,![]() .
.
Докажите, что если А – нормальный оператор, то нормальны также линейные операторы
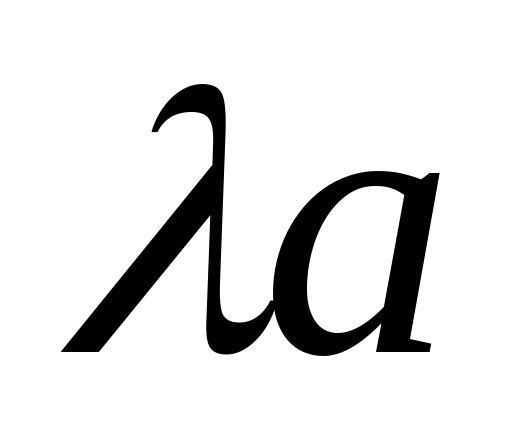 для любой константы
для любой константы ,
,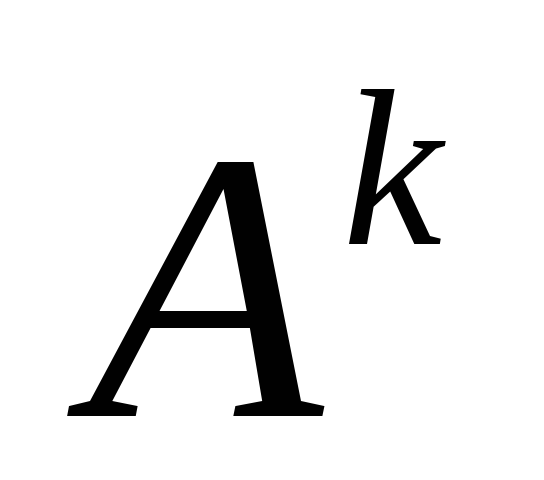 для
любого натуральногоk,
f(A)
для любого многочленаf(t),
для
любого натуральногоk,
f(A)
для любого многочленаf(t),
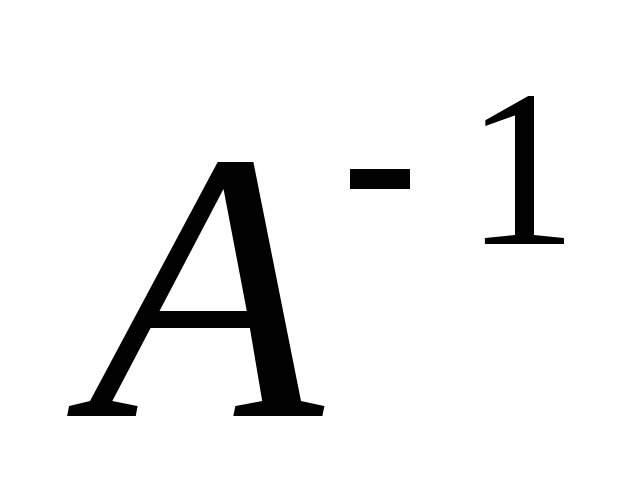 для
невырожденного оператораА,
для
невырожденного оператораА,
 .
.Для любого линейного оператора Аунитарного пространства существует полярное разложение в виде произведения неотрицательного и унитарного операторов. Докажите это.
Докажите, что ядро нормального оператора является ортогональным дополнением к его образу.
Докажите, что инвариантное подпространство нормального оператора инвариантно и относительно
 .
.
§4.1.7. Группа ортогональных матриц
Матрица Rназываетсяортогональной, если R-1 = RT.
Теорема. Матрица ортогональна тогда и только тогда, когда сумма квадратов элементов ее строки равна единице, а сумма произведений соответствующих элементов разных строк равна нулю.
Доказательство.
Необходимость следует из равенстваRRT
= I и из правила
умножения матриц строка на столбец.
Если же сумма квадратов элементов ее
строки равна единице, а сумма произведений
соответствующих элементов разных строк
равна нулю, тоRRT
= I
![]() R-1
= RT.■
R-1
= RT.■
Теорема. Матрица ортогональна тогда и только тогда, когда сумма квадратов элементов ее столбца равна единице, а сумма произведений соответствующих элементов разных столбцов равна нулю.
Доказательство проводится аналогично. ■
Упражнения
Докажите, что ортогональные матрицы одного порядка образуют мультипликативную группу.
Пусть А– комплексная
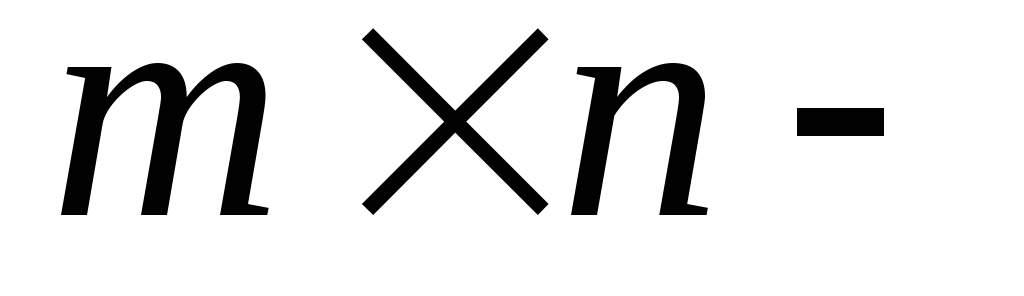 матрица.
Матрица
матрица.
Матрица строения
строения называетсясопряженной по отношению
к матрице А, если для всехi,
j
называетсясопряженной по отношению
к матрице А, если для всехi,
j
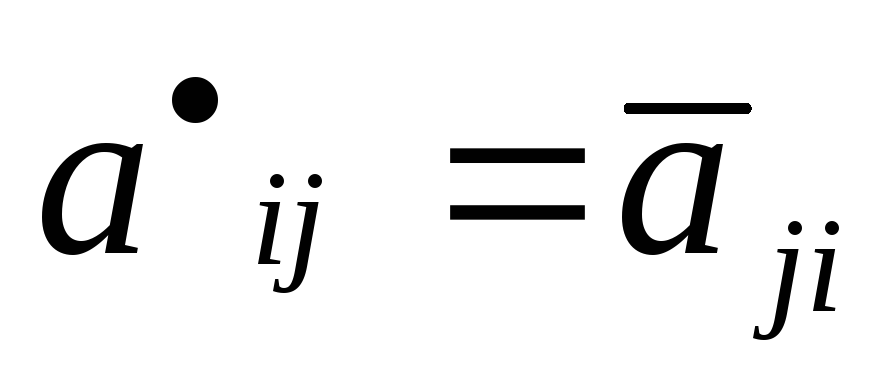 .
Докажите свойства:
.
Докажите свойства:
а)
![]() ;
;
б)
![]()
в)
![]() ;
;![]() ;
;
г)
![]()
д)
![]() ;
;
е) если
линейный оператор невырожден, то
![]() ;
;
ё)
![]() для любого целого неотрицательногоm.
для любого целого неотрицательногоm.
ж)
![]() для любого целогоm,
если матрицаАневырожденная;
для любого целогоm,
если матрицаАневырожденная;
з) если f(t)
=
![]() –произвольный многочлен, то
–произвольный многочлен, то![]() ,
где
,
где
![]() (х)
=
(х)
=
![]() .
.
Матрица Аназываетсянормальной, если
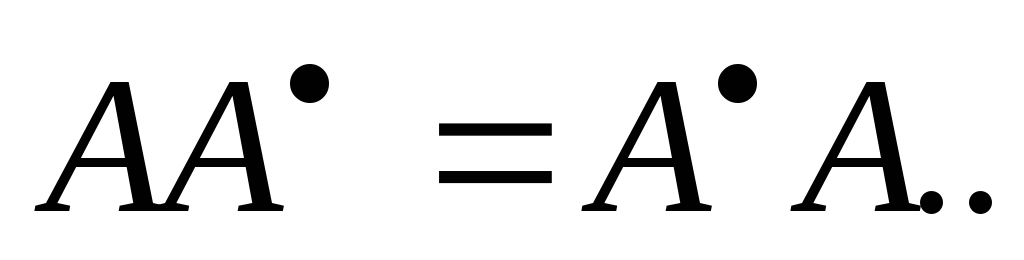 Докажите, что в нормальной матрице
скалярное произведение строкiиjравно скалярному
произведению столбцов i
и j.
Докажите, что в нормальной матрице
скалярное произведение строкiиjравно скалярному
произведению столбцов i
и j.Докажите, что в ортонормированном базисе унитарного пространства матрица нормального оператора нормальна. Обратно, нормальная матрица задает в ортонормированном базисе нормальный оператор.
Проверьте, что матрицы нормальные и для каждой найдите ортонормированный базис из собственных векторов
а)![]() ;
б)
;
б) ;
в)
;
в)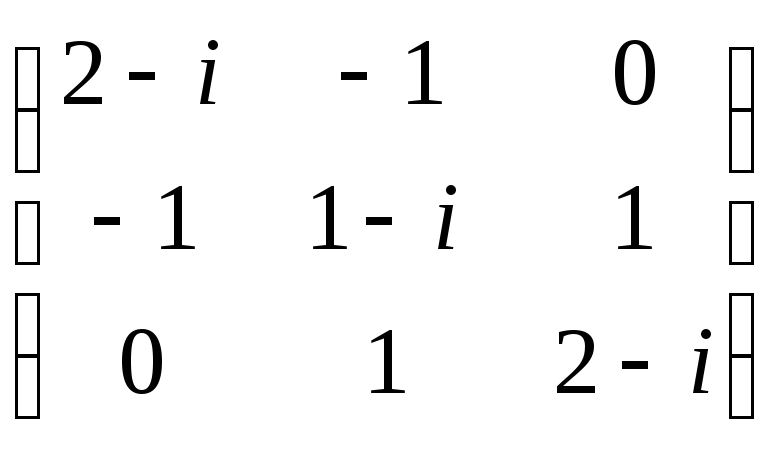 ;
г)
;
г)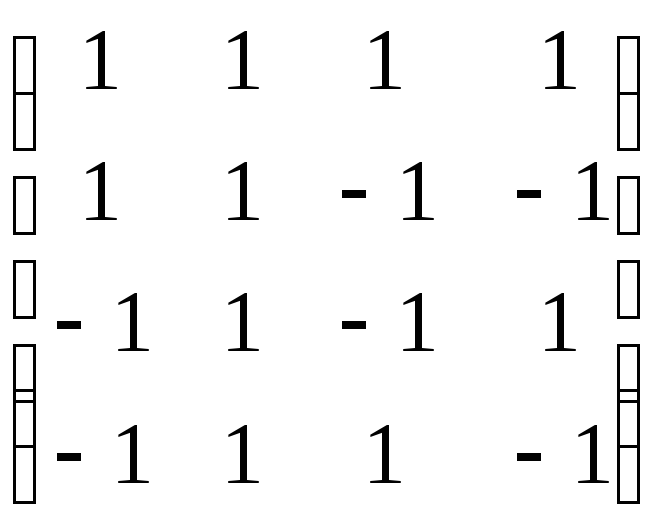 .
.
Матрица Uназываетсяунитарной, если
 Докажите, что матрица унитарна тогда
и только тогда, когда все ее собственные
значения по модулю равны единице.
Докажите, что матрица унитарна тогда
и только тогда, когда все ее собственные
значения по модулю равны единице.Докажите, что унитарные матрицы одного порядка образуют мультипликативную группу.
