Упражнения

1. Докажите, что квадратичная форма положительно определена тогда и только тогда, когда все корни характеристического многочлена ее матрицы положительны.

2. Квадратичная форма от nнеизвестных называетсяотрицательно определенной, если ее ранг равен отрицательному индексу инерции и равен числу неизвестных. Докажите, что квадратичная форма отрицательно определена тогда и только тогда, когда на любом ненулевом наборе значений переменных принимает отрицательные значения.

3. Квадратичная форма от nнеизвестных называетсянеотрицательной, если ее ранг равен положительному индексу инерции. Докажите, что квадратичная форма неотрицательна тогда и только тогда, когда на любом ненулевом наборе значений переменных принимает неотрицательные значения.

4. Квадратичная форма от nнеизвестных называетсянеположительной, если ее ранг равен отрицательному индексу инерции. Докажите, что квадратичная форма неположительная тогда и только тогда, когда на любом ненулевом наборе значений переменных принимает неположительные значения.

§4.2.5. Приведение квадратичной формы к главным осям

Теорема. (о приведении квадратичной формы к главным осям).Любую квадратичную форму с помощью ортогонального преобразования переменных можно привести к каноническому виду.

Доказательство. МатрицаАквадратичной формы симметрична, а для симметричной матрицы найдется ортогональная матрицаQ такая, что матрицаQ^{- 1}AQ диагональна. Подвергнув квадратичную форму ортогональному преобразованию с матрицейQ, мы приведем ее к каноническому виду. ■

Теорема. Квадратичная форма с помощью ортогонального преобразования переменных приводится к каноническому виду, коэффициентами которого являются корни характеристического многочлена матрицы квадратичной формы, взятые с их кратностями.

Доказательство. Пусть квадратичная формаf некоторым ортогональным преобразованием переменных приведена к каноническому виду

Легко видеть, что ортогональное преобразование оставляет инвариантной сумму квадратов переменных, поэтому

Квадрат определителя ортогональной матрицы равен 1. А определитель матрицы преобразованной квадратичной формы отличается от определителя матрицы исходной квадратичной формы на квадрат определителя матрицы линейного преобразования. Отсюда,

. ■

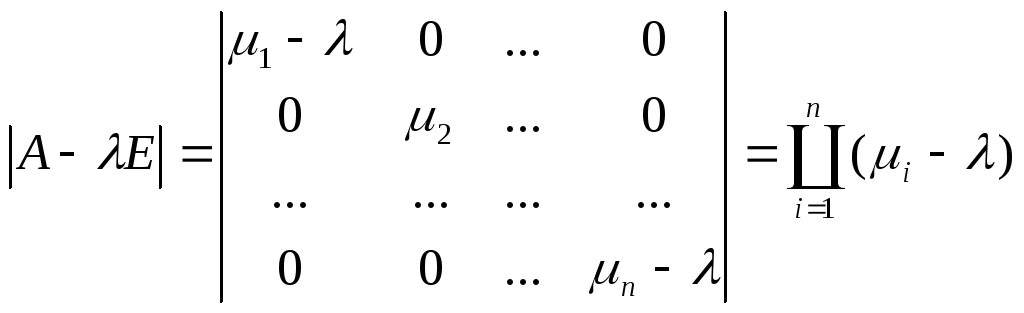Следствие. Для любой ортогональной матрицы, приводящей к диагональному виду симметрическую матрицу, на главной диагонали полученной диагональной матрицы располагаются характеристические корни симметрической матрицы, взятые с их кратностями.

Пример.Приведите к главным осям квадратичную форму

Матрица квадратичной формы имеет вид

А = .

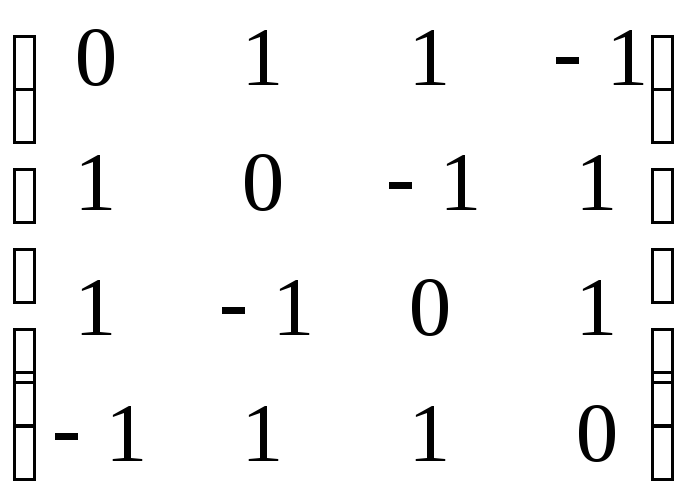Найдем ее характеристический многочлен

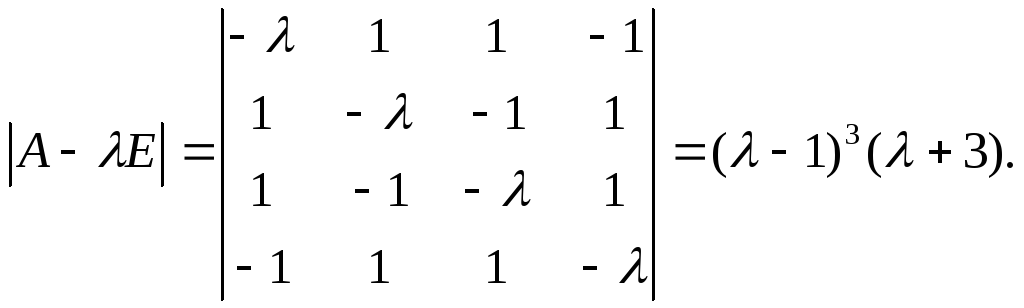
Матрица Аимеет трехкратный характеристический корень 1 и простой характеристический корень – 3. Таким образом,

–

канонический вид, к которому квадратичная форма приводится ортогональным преобразованием.

Для нахождения ортогонального преобразования, осуществляющего это приведение, необходимо найти собственные векторы линейного оператора, матрицей которого в некотором ортонормированном базисе является матрица А.Придля этого надо решить однородную систему линейных уравнений

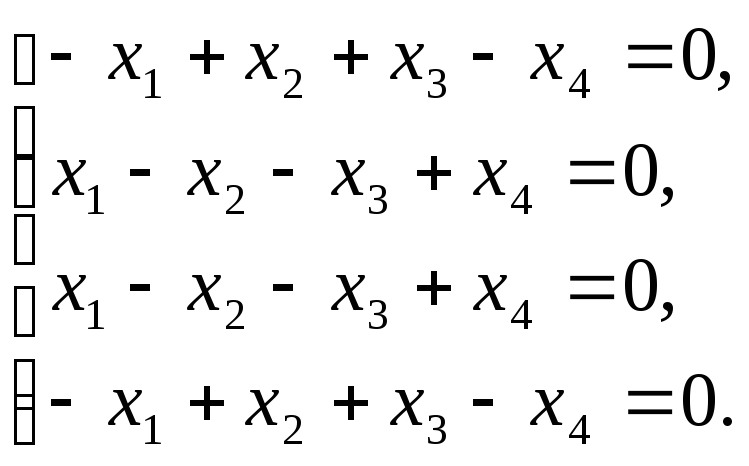
Ранг системы равен 1 и поэтому фундаментальная система решений состоит из трех решений. Например,

b₁= (1, 1, 0, 0),

b₂= (1, 0, 1, 0),

b₃= (-1, 0, 0, 1).

Ортогонализируя эту систему, получим

с₁ = b₁= (1, 1, 0, 0),

с₂= с₁+b₂= (,, 1, 0),

с₃=с₁+ с₃+b₃= (, , , 1).

При надо решить однородную систему линейных уравнений

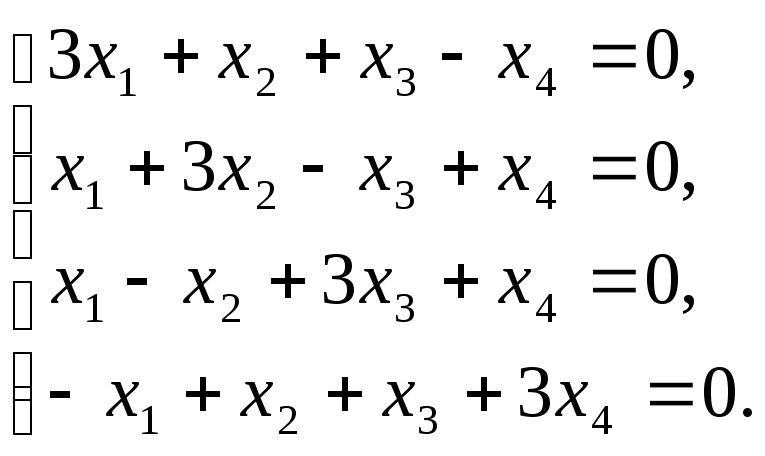
Ранг системы равен 3 и поэтому фундаментальная система решений состоит из одного решения. Например, с₄= (1, -1, -1, 1).

Нормируя ортогональную систему векторов с₁,с₂,с₃,с₄, получим ортонормированную систему векторов

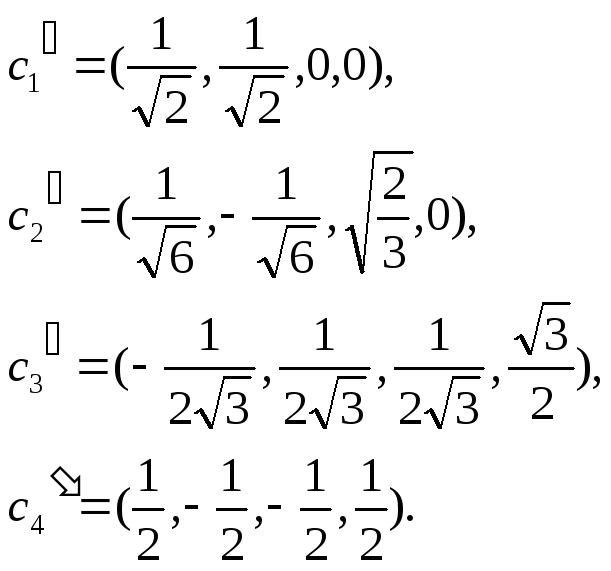
Таким образом, форма приводится к главным осям ортогональным преобразованием:

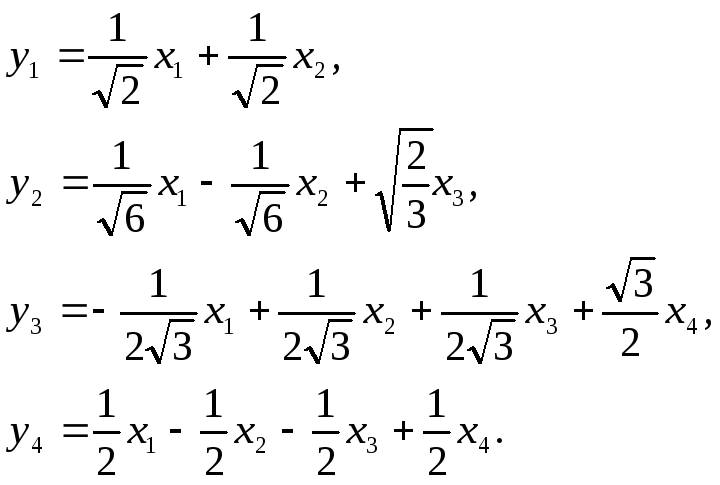
Следует отметить, что ответ неоднозначен.