
- •Модуль 4. Линейные операторы. Квадратичные формы Глава 4.1. Линейные операторы §4.1.1. Линейные операторы в линейном пространстве
- •Упражнения
- •§4.1.2. Ядро и образ линейного оператора
- •Упражнения
- •§4.1.3. Матрица линейного оператора
- •Упражнения
- •§4.1.4. Сумма и произведение линейных операторов
- •Упражнения
- •§4.1.5. Собственные векторы и собственные значения
- •Упражнения
- •§4.1.6. Самосопряженный линейный оператор
- •Упражнения
- •§4.1.7. Группа ортогональных матриц
- •Упражнения
- •§4.1.8. Ортогональный линейный оператор
- •Упражнения
- •Глава 4.2. Квадратичные формы
- •§4.2.1. Матричная запись квадратичной формы
- •Упражнения
- •§4.2.2. Теорема Лагранжа
- •Упражнения
- •§4.2.3. Закон инерции
- •Упражнения
- •§4.2.4. Положительно определенные квадратичные формы
- •Упражнения
- •§4.2.5. Приведение квадратичной формы к главным осям
- •§4.2.6. Билинейная форма
- •Упражнения
- •§4.2.7. Применение квадратичных форм к исследованию линий и поверхностей второго порядка
- •Упражнения
- •Глава 4.3. Каноническая форма Жордана
- •§4.3.1. Относительная линейная независимость
- •§4.3.2. Относительный базис
- •§4.3.3. Корневые векторы
- •Упражнения
- •§4.3.4. Корневое подпространство
- •Упражнения
- •§4.3.5. Канонический базис
- •§4.3.6. Циклическое подпространство
- •§4.3.7. Построение канонического базиса в корневом подпространстве
- •§4.3.8. Построение канонического базиса в общем случае
- •§4.3.9. Единственность канонической формы Жордана
Упражнения
Если А – линейный оператор евклидова пространстваV, тоf(x, y) = (Ax, y), g(x, y) = (x, Ay)– билинейные формы. Докажите это.
Докажите, что билинейная форма f(x, y) = (Ax, y) симметрична тогда и только тогда, когдаА – самосопряженный линейный оператор.
Пусть e1, e2, …, en и
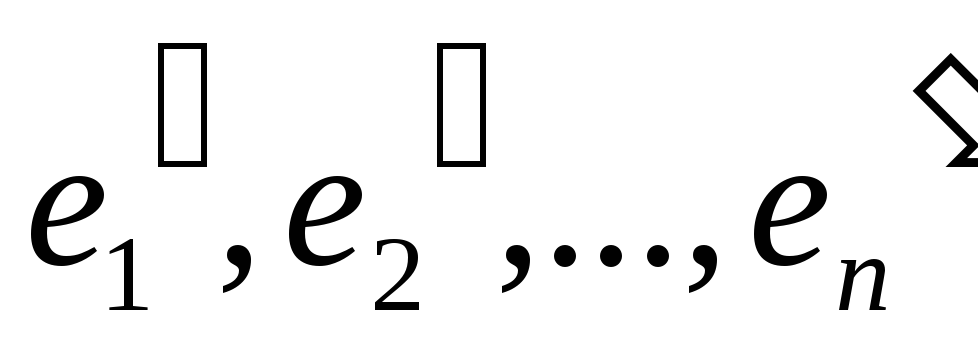 –
базисы линейного пространстваV,
С – матрица перехода от первого
базиса ко второму,А и
–
базисы линейного пространстваV,
С – матрица перехода от первого
базиса ко второму,А и –
матрицы билинейной формы в этих базисах.
Докажите, что
–
матрицы билинейной формы в этих базисах.
Докажите, что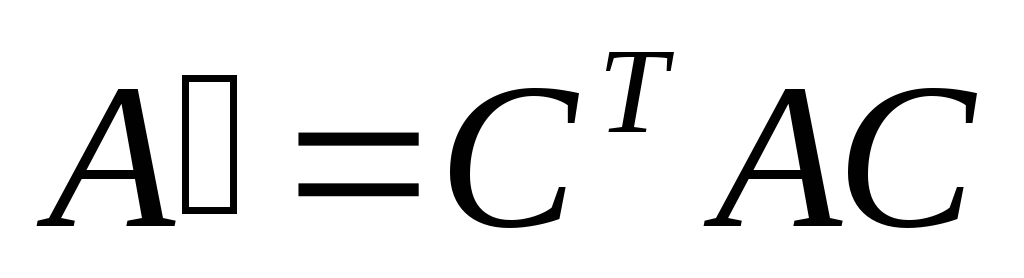 .
.Найдите матрицу билинейной формы и запишите соответствующую ей квадратичную форму а)
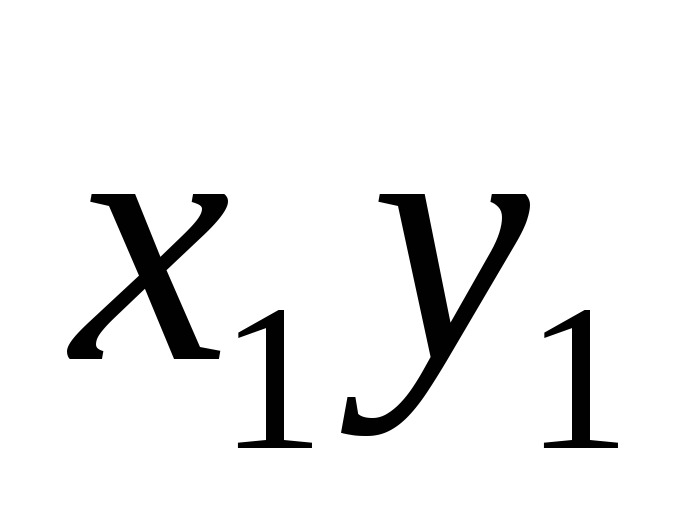 (
(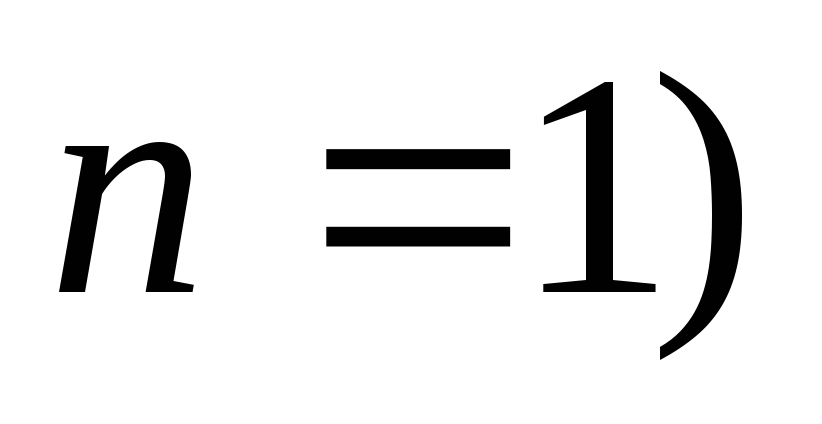 ;
б)
;
б)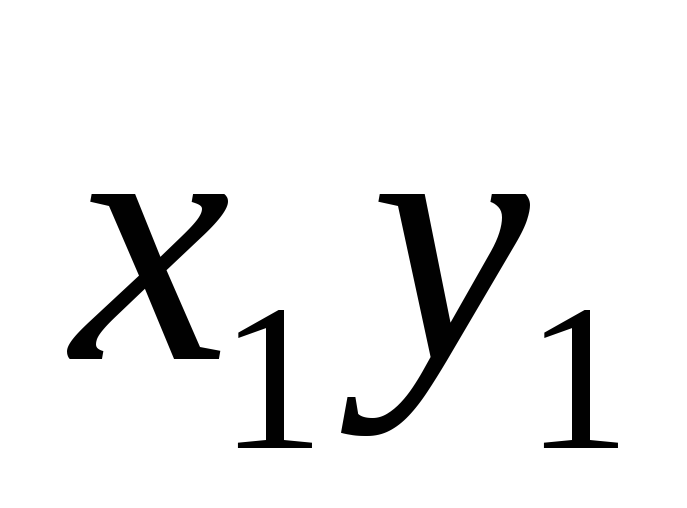 (
(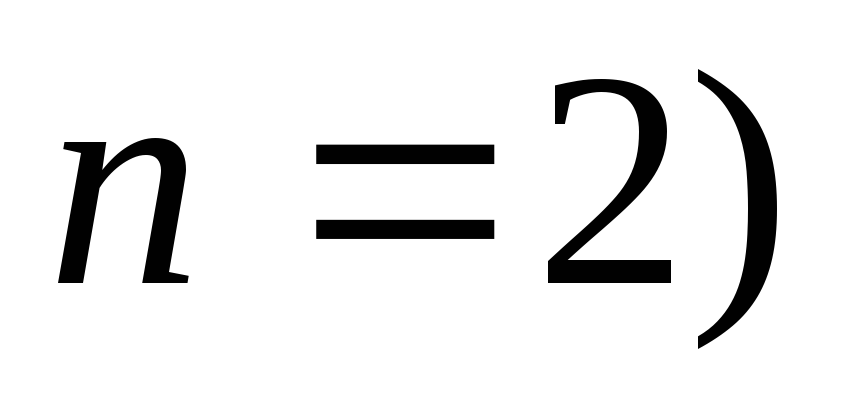 ;
в)
;
в)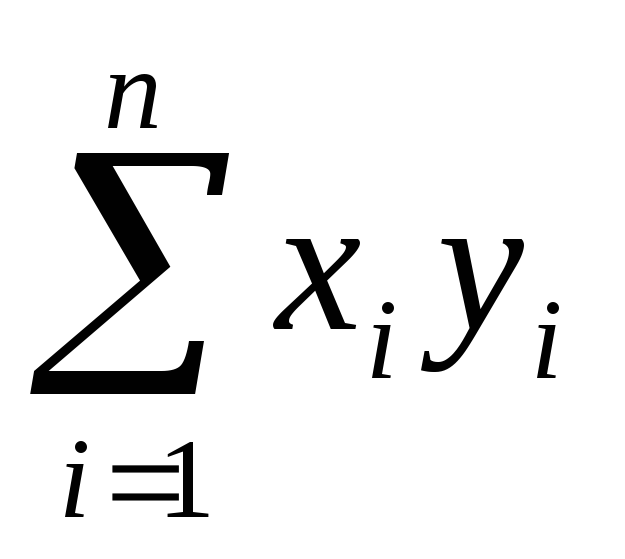 ;
г)
;
г)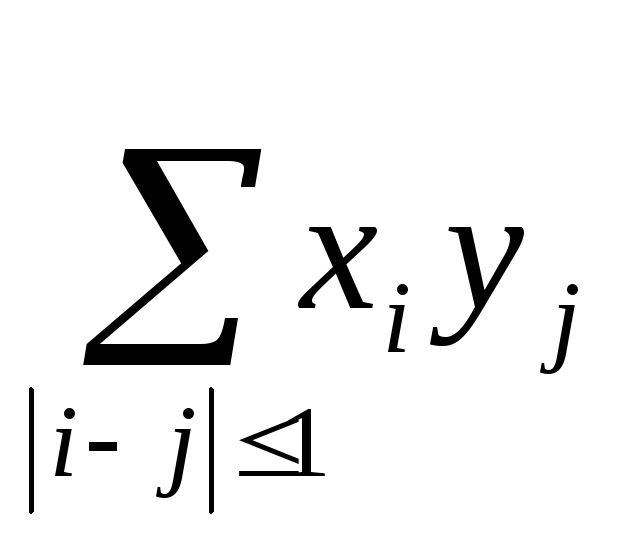 .
.Приведите с помощью невырожденного линейного преобразования переменных к каноническому виду (для которого матрица диагональная) билинейную форму:
а)![]() ;
б)
;
б)![]() ;
;
в)![]() .
.
Покажите, что функция
![]()
является симметричной билинейной формой
в пространстве многочленов степени
![]() .
Приведите ее к каноническому виду приn = 3.
.
Приведите ее к каноническому виду приn = 3.
Докажите, что ранг билинейной функции равен 1 тогда и только тогда, когда она является произведением двух ненулевых линейных функций.
Функция f(x, y) называется инвариантной относительно линейного оператора
 линейного пространстваV,
если
линейного пространстваV,
если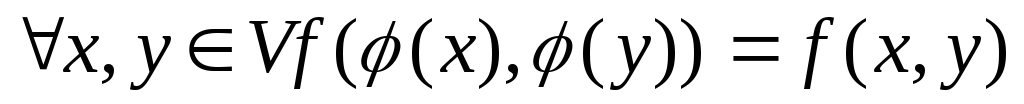 .
Докажите, что все невырожденные линейные
операторы, относительно которых функцияf(x,
y) инвариантна,
образуют мультипликативную группу.
.
Докажите, что все невырожденные линейные
операторы, относительно которых функцияf(x,
y) инвариантна,
образуют мультипликативную группу.Найдите все линейные операторы двумерного линейного пространства, относительно которых инвариантна билинейная форма
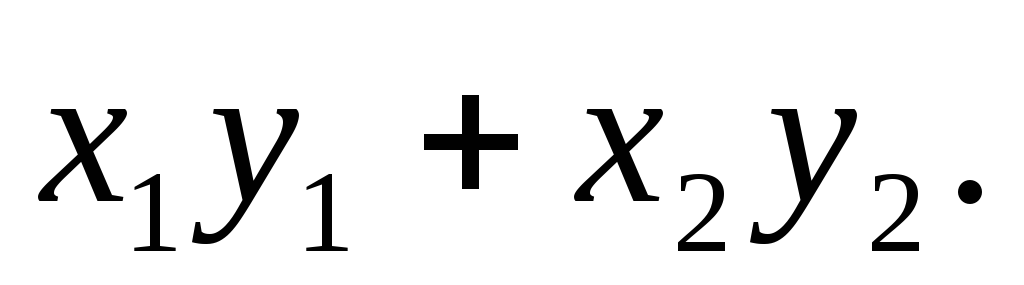
§4.2.7. Применение квадратичных форм к исследованию линий и поверхностей второго порядка
Общим уравнением второй степениназывается уравнение
F(x1, …, xn) = 0, (1)
где F(x1, …,xn) – многочлен второй степени отnпеременных x1, …,xn. МногочленF(x1, …,xn) можно представить в виде суммы квадратичной формыf, линейной формы (однородного многочлена первой степени) и свободного членас. Если черезАобозначить матрицу квадратичной формы f , черезХ – столбец неизвестныхx1, …,xn и черезВ – столбец из коэффициентовb1, b2, …, bn линейной формы, то в матричном виде многочленFможно записать в виде
F(x1, …,xn) =ХТАХ + 2ХТВ + с. (2)
При n = 2 уравнение (1) задает уравнение линии второго порядка на плоскостиR2, а при n = 3 – уравнение поверхности второго порядка в пространствеR3.
В аналитической геометрии для общего уравнения линии на плоскости или поверхности в пространстве ставится задача отыскания новой декартовой прямоугольной системы координат, в которой уравнение данной линии или поверхности принимает наиболее простой вид. Переход от одной декартовой прямоугольной системы координат к другой может быть осуществлен в два приема:
1) параллельный перенос начала координат в новую точку с сохранением направления осей;
2) поворот осей при сохранении начала.
Формулы параллельного переноса начала, выражающие старые координаты точки через ее новые координаты, имеют вид
xi
= vi
+ yi,
1![]() ,
,
где vi – координаты нового начала относительно старой системы координат (n =2 или 3). Если черезХ мы обозначим столбец из старых координат xi, через Y – столбец новых координат yi и через V – столбец из старых координат нового начала, то формулы параллельного переноса можно записать в виде матричного равенства
X = V + Y. (3)
Формулы поворота осей вокруг неподвижного начала в матричной форме могут быть записаны так
X = QY, (4)
где Q – ортогональная матрица второго или третьего порядка.
Решим задачу упрощения уравнения при произвольном n.Уточним предъявляемые требования:
избавиться от слагаемых, содержащих произведения разных переменных;
если возможно, то избавиться от слагаемых первой степени;
если возможно, то избавиться от свободного члена.
Уравнение, полученное при соблюдении этих требований, называется каноническим.
Задача. При помощи преобразованияX = QY с ортогональной матрицейQ в многочленеХТАХ + 2ХТВ + снельзя избавиться от слагаемых, содержащих переменные в первой степени. Докажите это.
Решение. ![]() .
Если в многочлене
.
Если в многочлене
ХТАХ + 2ХТВ
+ с есть слагаемые первой степени,
т.е.В
![]() ,то и в преобразованном многочлене
они есть.
,то и в преобразованном многочлене
они есть.
Задача. Всегда ли возможно при помощи преобразованияX = V + Y в многочленеХТАХ + 2ХТВ + сизбавиться от слагаемых, содержащих переменные в первой степени?
Решение. Подвергнем многочлен преобразованию
![]()
Как матрица квадратичной
формы матрица А симметрична. Матрица![]() первого порядка и поэтому совпадает со
своей транспонированной:
первого порядка и поэтому совпадает со
своей транспонированной:
![]()
Введем обозначение
![]() В преобразованном многочлене
В преобразованном многочлене
![]()
первые
степени отсутствуют, если столбец Vудовлетворяет условию![]() .
А это матричное уравнение относительно
неизвестного столбцаVне всегда разрешимо. При произвольном
столбцеВразрешимость можно
гарантировать лишь при невырожденной
матрицеА.Если матричное уравнение
разрешимо, то при помощи преобразования
.
А это матричное уравнение относительно
неизвестного столбцаVне всегда разрешимо. При произвольном
столбцеВразрешимость можно
гарантировать лишь при невырожденной
матрицеА.Если матричное уравнение
разрешимо, то при помощи преобразования![]() с ортогональной матрицейQмногочленFприводится
к каноническому виду. Этот случай
соответствует в аналитической геометрии
центральным линиям и поверхностям
второго порядка.
с ортогональной матрицейQмногочленFприводится
к каноническому виду. Этот случай
соответствует в аналитической геометрии
центральным линиям и поверхностям
второго порядка.
Предположим, что
уравнение
![]() не разрешимо относительно столбцаV.
Это может случиться только при
невырожденной матрицеА. Подвергнем
переменные многочлена (2) ортогональному
преобразованию, при котором квадратичная
форма
не разрешимо относительно столбцаV.
Это может случиться только при
невырожденной матрицеА. Подвергнем
переменные многочлена (2) ортогональному
преобразованию, при котором квадратичная
форма![]() примет
канонический вид. Так как рангr
матрицыАменьше ее порядка, то
числоrквадратов
переменных с отличными от нуля
коэффициентами в каноническом виде
меньшеnи в результате
преобразования многочлен примет вид:
примет
канонический вид. Так как рангr
матрицыАменьше ее порядка, то
числоrквадратов
переменных с отличными от нуля
коэффициентами в каноническом виде
меньшеnи в результате
преобразования многочлен примет вид:
![]()
где
![]() Можно избавиться от первых степеней
переменных
Можно избавиться от первых степеней
переменных![]() при помощи параллельного переноса
при помощи параллельного переноса
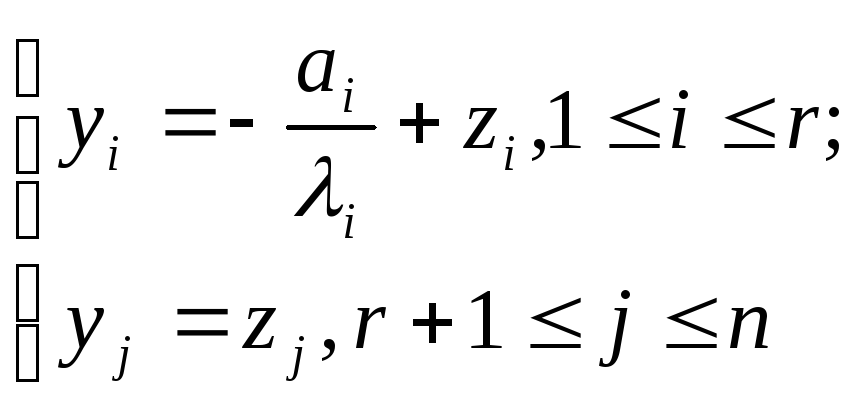
Многочлен примет вид
![]()
После преобразования
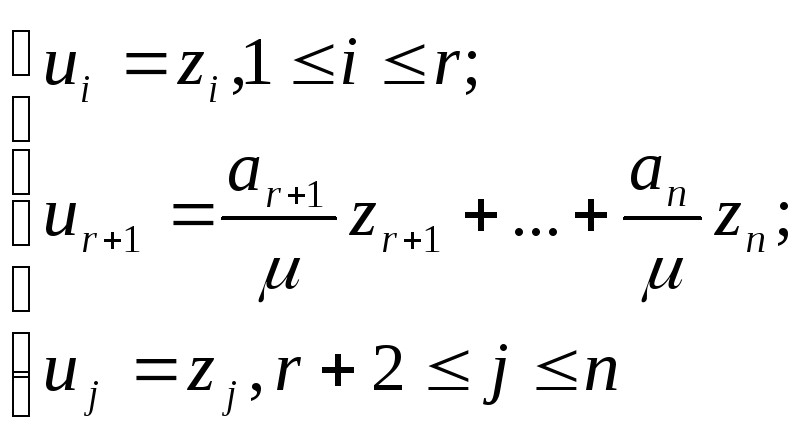
получим
![]() где
где![]() .
После выполнения параллельного переноса
.
После выполнения параллельного переноса

получим канонический вид
![]() .
.
Этот случай соответствует нецентральным линиям и поверхностям второго порядка.
Задача. Привести к каноническому виду уравнение линии:
![]()
Решение.
А =
![]() ,
В =
,
В =![]() ,V =
,V =
![]() .
.
Запишем матричное
уравнение
![]() в виде системы линейных уравнений
в виде системы линейных уравнений
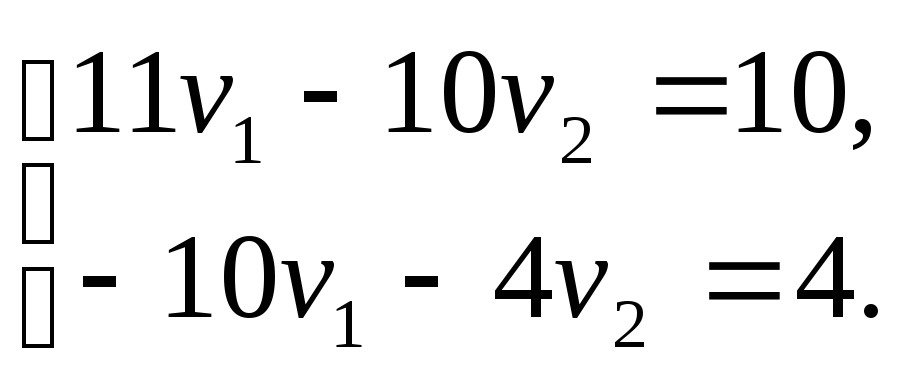
Система крамеровского
типа имеет единственное решение
![]() линия имеет единственный центр. После
параллельного переноса начала системы
координат в этот центр
линия имеет единственный центр. После
параллельного переноса начала системы
координат в этот центр
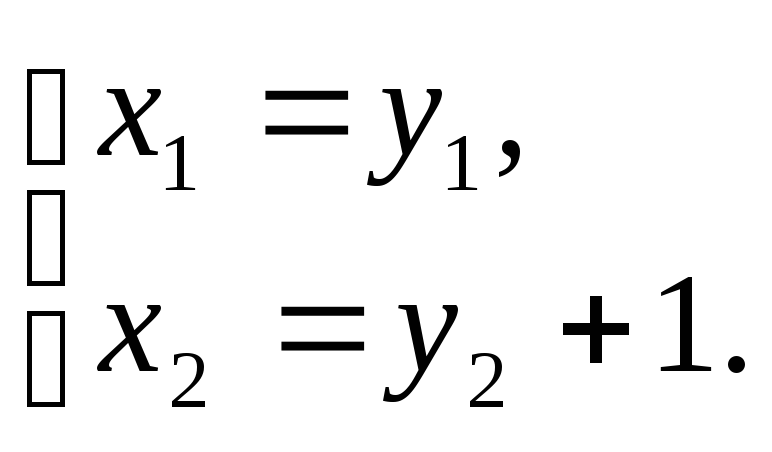
уравнение линии примет вид
![]()
Совершим ортогональное
преобразование Y =
QZ (поворот
системы координат), приводящее квадратичную
формуf = ![]() к каноническому виду. В ортонормированном
базисе
к каноническому виду. В ортонормированном
базисе![]() двумерного евклидова пространстваR2
существует и притом единственный
линейный оператор
двумерного евклидова пространстваR2
существует и притом единственный
линейный оператор![]() ,
имеющий в этом базисе матрицуА =
,
имеющий в этом базисе матрицуА =
![]() квадратичной формыf.
Так как матрицаА симметрична, то
линейный оператор
квадратичной формыf.
Так как матрицаА симметрична, то
линейный оператор![]() самосопряжен и существует ортонормированный
базис
самосопряжен и существует ортонормированный
базис![]() из его собственных векторов. Матрица
перехода от базиса
из его собственных векторов. Матрица
перехода от базиса![]() к базису
к базису![]() и есть искомая матрицаQ.
и есть искомая матрицаQ.
Составим и решим характеристическое уравнение матрицы А:
![]() или
или![]()
Его корни
![]() После
применения ортогонального преобразованияY = QZк уравнению
После
применения ортогонального преобразованияY = QZк уравнению![]() оно примет вид
оно примет вид
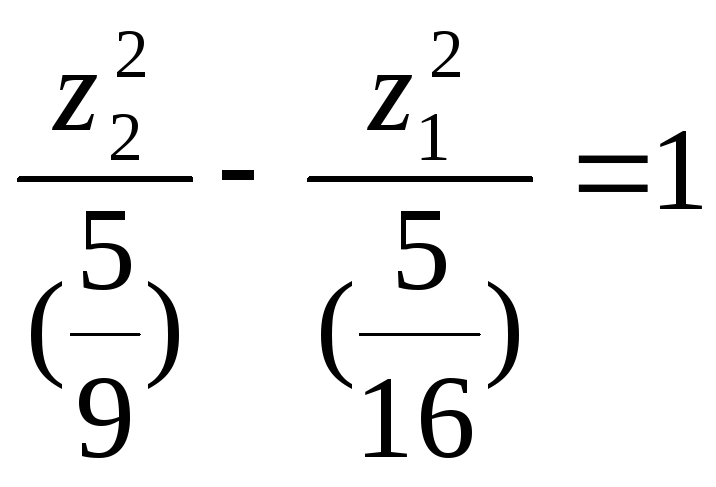 .
.
Это каноническое уравнение гиперболы.
Найдем матрицу Q
ортогонального преобразования
переменных. Для этого прежде всего надо
найти базис подпространства собственных
векторов линейного оператора![]() ,
принадлежащих собственному значению
,
принадлежащих собственному значению![]() .
Если
.
Если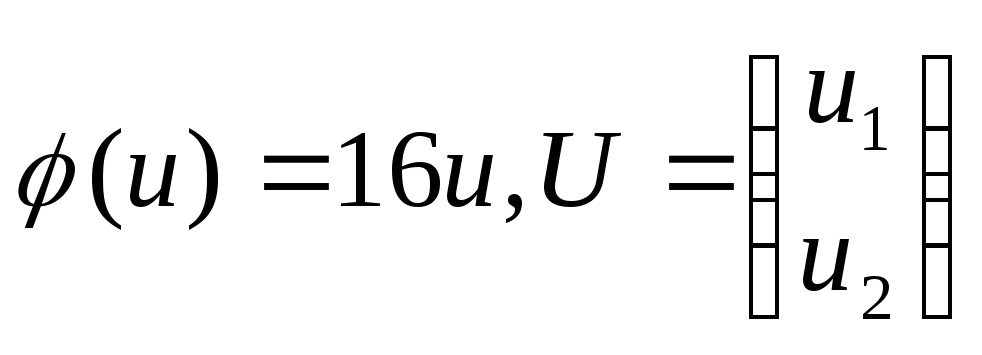 ,
то
,
то![]() или
или
 .
.
Общее решение системы
![]() любое
число. Фундаментальная система решений
состоит из одного вектора, например,f1=
любое
число. Фундаментальная система решений
состоит из одного вектора, например,f1=![]() .
Пронормировав его, получим
.
Пронормировав его, получим![]() .
Аналогично найдем базис подпространства
собственных векторов, принадлежащих
собственному значению
.
Аналогично найдем базис подпространства
собственных векторов, принадлежащих
собственному значению![]() Это, например,f2=
Это, например,f2=![]() .
Векторы
.
Векторы![]() образуют ортонормированный базис R2,
составленный из собственных векторов
линейного оператора
образуют ортонормированный базис R2,
составленный из собственных векторов
линейного оператора![]() .
Матрица ортогонального преобразованияQ составляется из
координатных столбцов векторов
.
Матрица ортогонального преобразованияQ составляется из
координатных столбцов векторов![]() :
:
Q = ![]() .
.
Выпишем линейное преобразование переменных, приводящее уравнение к каноническому виду

