4.3. Предикаты и кванторы

Предикатном называется n – местная функция P (x₁,…,x_n), которая при подстановки вместо символов переменных конкретных значений из некоторого множества M превращается в высказывание, т.е. принимает значение “истина” или “ложь”. Множество М, из которого применяют значения предикатные переменные x₁,…,x_n, называется предметной областью предиката.

Пусть, например, P(X) обозначает одноместных предикат “x –простое число ”, предметная область M = {2,3,4…}. Тогда P(2) = “истина”, P(3) = “истина”, P(4) = “ложь”.

Пусть P(x,y) - двухместный предикат “xy”. Тогда P (3,5) = “истина”, P(5,3) = “ложь”.

Множество тех наборов значений аргументов, на которых предикат принимает значение “истина”, называется областью истинности этого предиката. Область истинности двухместного предиката является бинарным отношением.

Квантор общности. Пусть P (x) – некоторые предикат, принимающий значение “истина”, или “ложь”, для каждого элемента x множества M. Тогда под выражением (x) P(x) будем подразумевать высказывание истинное, когда P(x) истинно для каждого элемента х из множества М, и ложное – в противном случае. Читается это выражение так: “для всех х P(x)”. Это высказывание уже не зависит от х. Символ x называется квантором общности.

Квантор существования. Пусть P(x)-некоторый предикат. Под выражением (х) Р(х) будем понимать высказывание истинное, когда существует элемент множества М, для которогоP(x) истинно, и ложное в противном случае. Читается это выражение так: «Существует х такое, что Р(х)» или существует х, для которого Р(х). Символ х называется квантором существования.

Покажем как определяющие алгебраическую группу условия ассоциативности, существования единичного и обратного элементов запишутся на языке кванторов:

(x) (y) (z) (xy)z=x(yz)

(e) (x) ex=xe=x

(x) (x^-1) x^-1 x=xx^-1=e

Контрольные вопросы.

1. Дайте определение высказывание.

2. Перечислите наиболее известные тавтологии.

3. Перечислите основные методы доказательств. В чем суть каждого метода?

4. Что такое предикат?

5. Какие кванторы вы знаете?

Тест IV.

1. Высказыванием называется утверждение, имеющее значение: а)истина; б)ложь; в)истина или ложь.

2. Каким значком обозначают импликацию: а); б); в)().

3. Для логического значка “~” принято следующие чтение: а)”…или...“; б):”...если..., то...,”; в) “тогда и только тогда, когда...”.

4. Квантор читается: а) для всех; б)существует; в)найдется.

5.Высказывание: “существует вещественное число x, удовлетворяющее уравнению х²+1=0” в символической форме записывается:

а) б);

в)

Глава 5. Алгоритмы и машина Тьюринга.

5.1. Понятие алгоритма.

Алгоритм- это точное предписание, задающее процесс решения задачи. Алгоритм задаётся набором инструкций, последовательные выполнения которых являются элементарными шагами алгоритма. Процесс начинается с исходных данных, выделяющих данную индивидуальную задачу из множества задач, решаемых алгоритмом, и направлен на получение полностью определяемого этими исходными данными результата. Примерами алгоритмов являются изучаемые в школе правила сложения, вычитания, умножения и деления столбиком. Здесь исходными данными служат упорядоченные пары натуральных чисел, записанные в десятичной системе, а результатом - также натуральное число в десятичной системе. Само слово алгоритм происходит от имени среднеазиатского математика Мухаммеда бен Мусы аль – Хорезми, давшего в 825 году правила выполнения 4 арифметических действий в десятичной системе. Понятие алгоритма является одним из важнейших в современной математике. С появлением вычислительных машин понятие алгоритма тесно связано с программированием, так как программа на ЭВМ является формой представления алгоритма на некотором алгоритмическом языке программирования.

Теория алгоритмов в настоящее время – это обширная область математики. Одним из важнейших вопросов в ней является вопрос алгоритмической разрешимости определённого класса задач. Были найдены классы задач, для решения которых не существует алгоритма, так называемые алгоритмически неразрешимые проблемы.

Пусть, например, требуется установить, имеет ли целые корни данное алгебраическое уравнение

а₀ xⁿ + а₁ x^n-1 +…+ а_n-1 x + а_n =0

с целым коэффициентами a₀, a₁,...,a_n.

Алгоритм для решения этой задачи существует, так как если это уравнение имеет целый корень р, то р должно быть делителем числа a_n. Поэтому для данного уравнения можно найти все делители числа a_n и все по очереди проверить. Однако, аналогичная проблема для уравнений P(x₁,...,x_m)=0, где P(x₁,...,x_m) – произвольный многочлен с целыми коэффициентами от любого числа m неизвестных, оказалась алгоритмически неразрешимый. Получение подобных результатов, относящихся к неразрешимости определённого класса задач, потребовало уточнения понятия алгоритма. Одним из возможных и используемых в математике подобных уточнений является рассматриваемая далее машина Тьюринга.

В тех же случаях, когда сама разрешимость не вызывает сомнений, центральным в теории алгоритмов становится вопрос трудоёмкости решения, т.е. оценка числа элементарных операций, выполняемых алгоритмом при решении задачи. Пусть U – множество решаемых задач, А – множество алгоритмов, решающих задачи данного класса, N (a,u) – число элементарных операций, выполняемых алгоритмом aA при решении задачи uU. Тогда в качестве эффективности алгоритма а можно взять число операций на самой трудной для него задаче из данного класса N (a,u). Если теперь выбрать из множества возможных алгоритмов алгоритм, для которого эта величина принимает минимальное значение, то получиться величина N (a,u), которая уже не зависит ни от u, ни от а, а характеризует трудоёмкость задач класса U в целом.

На самом деле класс решаемых задач U состоит, как правило, из однотипных задач различной размерности, и трудоёмкость решения индивидуальной задачи в значительной степени определяется её размерностью. Так, трудоёмкость выполнения арифметических действий зависит от величины участвующих в них чисел. Поэтому задачи класса U разбиваются на подклассы по размерности задач, и трудоёмкость определяется для каждого из подклассов как функция размерности. Скорость роста этой функции и характеризует сложность решения задач данного класса.

Рассмотрим эти понятия на примере простого, но чрезвычайно важного как с теоретической, так и с практической точек зрения алгоритма Евклида для нахождения наибольшего общего делителя двух натуральных чисел.

5.2. Алгоритм Евклида.

Пусть даны два натуральных числа n и m, причём n  m. Требуется найти их наибольший общий делитель d = (n, m). Способ для решения этой задачи, приведённый в книге Начала Евклида, состоит в следующем. Делим число n на m с остатком. Это даёт n = k₁m + r₁, где частное k₁ является целым положительным числом, а остаток r₁ – либо 0, либо положительное число, меньше m, 0 r₁m. Если остаток не равен нулю, то повторяем операцию деления с остатком, но делимым является делитель предыдущего шага, а делителем – его остаток, и так до тех пор, пока не получиться остаток, равный нулю. Последний, положительный остаток в этом процессе и является наибольшим общим делителем чисел n и m. Процесс может быть описан следующей цепочкой равенств:

n = k₁m + r₁

m = k₂ r₁ + r₂

r₁ = k₃ r₂ + r₃

r₂ = k₄ r₃ + r₄



r_l-4 = k_l-2 r_l-3 + r_l-2

r_l-3 = k_l-1 r_l-2 + r_l-1

r_l-2 = k_l r_l-1

r_l-1 = (n, m)

Компактно алгоритм Евклида может быть представлен следующей блок-схемой:

Начало

n, m

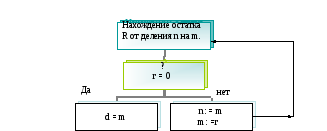
Конец

(n, m) = d

Циклически повторяемая операция деления с остатком является фактически единственной операцией этого алгоритма. Поэтому число её повторений может служить естественной мерой трудоёмкости алгоритма Евклида.

Так как r₁  n/2, то делимое за 2 шага уменьшается более чем вдвое. Поэтому число шагов алгоритма l может быть оценено сверху как

l  2 log₂ n. Если число n представлена в десятичной системе исчисления, то, как показывает данная оценка, число шагов ограничено линейной функцией от длины записи числа n. Поэтому алгоритм Евклида очень эффективный алгоритм. Намного более трудоёмким было бы нахождение наибольшего общего делителя с помощью разложения чисел m и n на простые множители.

Алгоритм Евклида можно применять также для нахождения наибольшего общего делителя двух многочленов и общей меры двух соизмеримых отрезков. Если отрезки несоизмеримы, т.е. их отношение выражается иррациональным числом как, например, у стороны квадрата и его диагонали, то алгоритм Евклида приводит к бесконечному процессу.

Для обоснования алгоритма Евклида достаточно заметить, что из равенства n = k₁m + r₁ вытекает, что каждый делитель чисел m и n является делителем чисел m и r₁ и наоборот, следовательно (n, m) = (m, r₁).

Поэтому суть алгоритма Евклида в том, он сводит задачу нахождения наибольшего общего делителя двух чисел к аналогичной задаче для меньших чисел.

Из алгоритма Евклида можно сделать ещё один чрезвычайно важный вывод, а именно, (m, n) выражается линейно через m и n:

(m, n) = sn + tm, где s и t – целые числа.

В самом деле, из первого равенства цепочки получаем r₁ = n – k₁m, т.е. r₁ линейно зависит от n и m. Из второго равенства r₂ = m – k₂ r₁, т.е. r₂ линейно зависит от m и r₁, но r₁ линейно зависит от n и m, поэтому r₂ также линейно зависит от n и m:

r₂ = m – k₂ (n – k₁m) = (k₁ k₂ + 1)m - k₂ n. продолжая движение по цепочке, окончательно получаем, что наибольший общий делитель двух чисел линейно с целыми коэффициентами через них выражается.

В заключение приведём численный пример использования алгоритма Евклида. Пусть требуется найти наибольший общий делитель чисел 7200 и 3132. Последовательные шаги алгоритма в этом случае таковы:

7200 = 2 * 3132 + 936

3132 = 3 *936 + 324

936 = 2 * 324 + 288

324 = 1 * 288 + 36

288 = 8 *36

(7200, 3132) = 36.