Контрольные вопросы.

1. Какую функцию называют булевой?

2. Какое множество является областью определения и областью значений булевой функции?

3. Какие 3 операции над булевыми функциями задают булеву алгебру?

4. Дайте определение д.н.ф. и к.н.ф.

5. Опишите механизм упрощения д.н.ф.

Тест III

1. Булевой функцией от n переменных называется функция, определенная на множестве всех двоичных наборов длины n и принимающая на каждом из них значение.

а) 0; б) 1; в) 0 или 1; г) любые целые;

2. Булева функция называется монотонной, если из х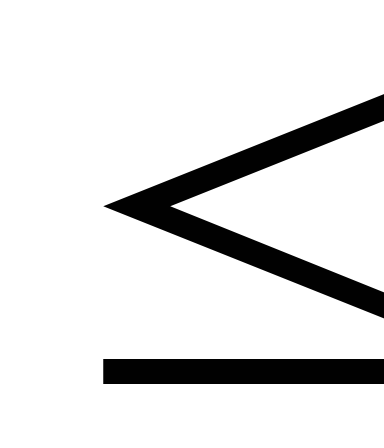у следует

а)б)>; в); г)<;

3. Выражение 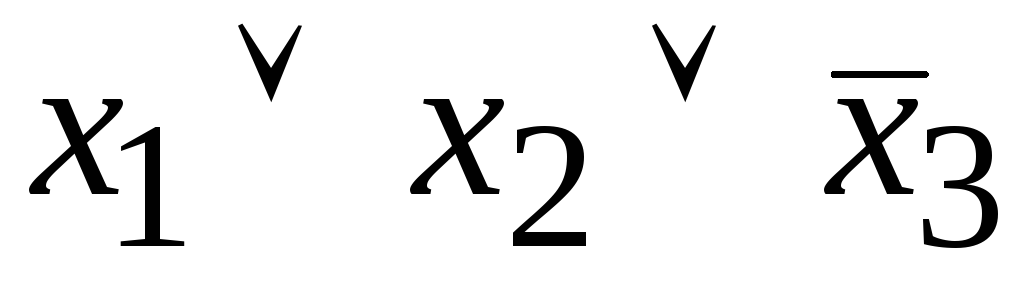называют

а) элементарной дизъюнкцией; б) элементарной конъюнкцией.

4. Результатом упрощения д.н.ф. 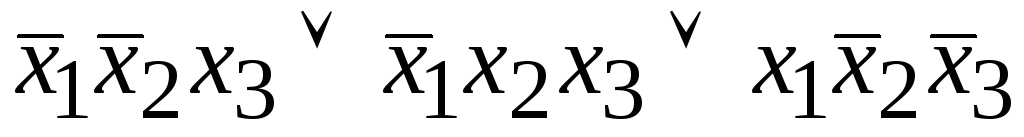является форма:

а) б); в).

5. Функцией, двойственной к функции , является

а)б)в)

Глава IV. Элементы математической логики

4.1. Исчисление высказываний.

Под высказыванием понимается языковое предложение, о котором есть смысл говорить, что оно истинно или ложно. Например: Москва-столица России, Вашингтон-столица США, Рим-столица Франции. Первые два из этих высказываний истинны, третье ложно.

Из подобных простых высказываний могут быть образованы сложные с помощью частицы “не” и связок: “и”; “или”; “если…то”; “тогда и только тогда, когда”. Считая истину и ложь булевыми переменными, причем истина – это 1, а ложь – 0, перечисленные связки можно отождествить с логическими операциями отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности. При этом часто встречающиеся в обыденные речи союзы “а” и “но”, также отождествляются с конъюнкцией, не обращая внимания на нюансы смысловых оттенков. Истинность или ложность подобных составных высказываний может быть установлена с помощью приведенной в 1 главе III таблицы.

Обозначим 3 приведенных выше высказывания соответственно буквами P,Q и R. Тогда высказывания: Москва – столица России, Вашингтон – столица США, но Рим – не столица Франции, запишется как PQ. Это высказывание мы считаем истинным. Истинными будут также высказывания PQ,P, Q,, а ложными – P&, , P&Q&R.

Пусть P теперь обозначает высказывание “я устал”, Q- “я голоден”,

R –“ я не могу заниматься”. Тогда высказывание “если я устал или голоден, я не могу заниматься”, запишется в виде (RQ)R. А высказывание “я могу заниматься тогда и только тогда, когда я не устал и не голоден” – в виде (P&Q) ~ .

4.2. Логическое следствие

Вопрос истинности или ложности элементарных высказываний P, Q и R находится за пределами математической логики, основное внимание которое концентрируется на способах получения из заданного множества высказываний, считающихся истинными, новых высказываний.

Особую роль при этом играют тождественно-истинные формулы, справедливые при любом приписывании и играющие роль логических законов. Они называются тавтологиями. К числу наиболее известных тавтологий относятся:

(P ) – закон исключенного третьего;

( ~ P) – закон двойного отрицания;

() - закон противоречия.

При доказательстве теорем в различных разделах математики используется небольшое число типичных схем рассуждения, которое можно выразить формулами. Рассуждение называется правильным, если из конъюнкции посылок следует заключение, т.е. всякий раз, когда все посылки истинны, заключение тоже истинно.

Пусть P₁,…,P_n -посылка , D – заключение. Тогда для определения правильности рассуждения , т.е. утверждения о том, что из данных посылокP₁,…,P_n следует заключение D, требуется установить тождественную истинность импликации (P₁&…&P_n)  D.

В качестве примера рассмотрим рассуждение:

Если Петр занимается спортом, то Петр никогда не болеет. Петр занимается спортом. Следовательно, Петр никогда не болеет.

Это рассуждение по схеме.

Формула ((A  B) & A)  B является тавтологией, и, значит, рассуждение правильное.

В качестве ошибочного рассуждения можно привести слегка измененный пример:

Если Петр занимается спортом, то Петр никогда не болеет. Петр никогда не болеет. Следовательно, Петр занимается спортом

Это рассуждение по схеме . Но формула ((A  B) & B)  A не является, как легко проверить, тавтологией. Поэтому это неверное рассуждение. Петр может как заниматься, так и не заниматься спортом.

Распространенной схемой правильных рассуждений является также

, которая основана на тавтологии ((A  B) &

Если требуется доказать истинность высказывания вида A  B, где

A – конъюнкция посылок, B – заключение, то нередко оказывается удобнее доказывать истинность другой импликации, равносильной исходной. Известной схемой рассуждения подобного рода является контрапозиция, когда вместо импликации A  B доказывается импликация . Контрапозиция основана на тавтологии.

Другим известным приемом доказательства импликации A  B является метод доказательства от противного, когда допускают, что импликация A  B ложно и приходя к противоречию, заключающемуся в том что некоторые высказывания истинно и ложно одновременно (C &). Этот метод основан на тавтологии (A  B) ~ (() (C & )) ~((A&) (C & )). Именно этим путем была доказана не равномощность множествA и 2^A в §5 главы 1.

В обыденной жизни также бывают ситуации, когда пригодится из суждений, считающихся истинным, извлекать логические следствия. Это легче всего делать также доказательством от противного. Считая следствие ложным, приходят либо к доказывающему следствие противного, либо к приписыванию простым компонентам суждений истинностных значений, совместимых с отрицанием следствия. Последнее показывает, что рассуждение не логично. В качестве примера рассмотрим следующее рассуждение.

Если я пойду завтра на первое занятие, то должен буду встать рано, а если я пойду вечером на танцы то лягу спать поздно. Если я лягу спать поздно, а встану рано, то я буду вынужден довольствоваться пятью часами сна. Я просто не в состоянии обойтись пятью часами сна. Следовательно, я должен или пропустить завтра первое занятие, или не ходить на танцы.

Чтобы исследовать, справедливо ли это рассуждение, символизируется его, заменяя простые высказывания буквами. Пусть C означает “Я пойду завтра на первое занятие”; G – “Я должен встать рано”; D – “Я пойду вечером на танцы”; S – “Я лягу спать поздно”, а E – “Я могу обойтись пятью часами сна ”. тогда посылки можно записать символически в следующем виде:

(C  G) & (D  S),

S & G  E,

,

а исследуемое заключение примет вид

.

Следуя описанному выше методу анализа, примем, что каждая из посылок истинна, а заключение ложно. Тогда и C и D должны иметь значение “истина”. Далее, из первой посылки следует, что G и S также имеют значение “истина”. Это и вторая посылка влечет за собой, что E имеет значение “истина”. Но это противоречит допущению что третья посылка имеет значение “истина”.

Таким образом, доказано, что заключение является логическим следствием имеющихся посылок.