
- •Министерство образования российской федерации
- •Содержание.
- •Глава I. Множества.
- •1.1. Определения и обозначения.
- •1.2. Операции над множествами.
- •1.3. Свойства операций
- •1.4. Мощность множества.
- •1.5. Прямое произведение множеств.
- •Глава II. Отношения, функции, алгебраические
- •2.1. Бинарные отношения.
- •2.2. Функции.
- •2.3. Алгебраические структуры и морфизмы.
- •Отношение конгруэнтности позволяет определить так называемую фактор-структуру, носителем которой является множество классов эквивалентности. Приведём примеры.
- •Контрольные вопросы
- •Тест II
- •Глава III. Булевы функции.
- •3.1. Определение и основные свойства.
- •3.2 Дизъюнктивная и конъюнктивная нормальные формы
- •3.3. Упрощение д.Н.Ф.
- •Контрольные вопросы.
- •Тест III
- •Глава IV. Элементы математической логики
- •4.1. Исчисление высказываний.
- •4.2. Логическое следствие
- •4.3. Предикаты и кванторы
- •Тест IV.
- •Глава 5. Алгоритмы и машина Тьюринга.
- •5.3. Машина Тьюринга.
- •F : q a a
- •5.4. Алгоритмически неразрешимые проблемы.
- •Итоговый тест.
- •Рекомендуемая литература. Основная:
- •Дополнительная
- •Словарь основных терминов
- •Ответы к тестам
- •Зуев Юрий Анатольевич Садыкова Альбина Рифовна Математическая логика и теория алгоритмов. Теория множеств. Дискретная математика
Глава I. Множества.
1.1. Определения и обозначения.
Множество – это собрание определённых и различимых между собой объектов, мыслимых как единое целое. Объекты, называемые элементами множества, могут иметь физическую природу (яблоки, песчинки, люди, звёзды) или быть продуктом нашего интеллекта (числа, фигуры, буквы).
Множества
обозначаются большими латинскими
буквами А![]() ,
В, С, ...
, а их
элементы – малыми буквами, обычно
одноимёнными. Запись А={a1,...,an}
означает, что множество А
состоит из элементов a1,...,an.
Запись aА
означает, что элемент a
принадлежит множеству А.
Множество, не содержащее ни одного
элемента, называется пустым и обозначается
,
В, С, ...
, а их
элементы – малыми буквами, обычно
одноимёнными. Запись А={a1,...,an}
означает, что множество А
состоит из элементов a1,...,an.
Запись aА
означает, что элемент a
принадлежит множеству А.
Множество, не содержащее ни одного
элемента, называется пустым и обозначается
![]()
. Запись В
. Запись В![]() А
означает, что множество В
является подмножеством множества А,
т. е. каждый элемент множества В
является элементом множества А.
Само множество А
и
называются несобственными подмножествами
множества А,
все остальные подмножества – собственные.
А
означает, что множество В
является подмножеством множества А,
т. е. каждый элемент множества В
является элементом множества А.
Само множество А
и
называются несобственными подмножествами
множества А,
все остальные подмножества – собственные.
1.2. Операции над множествами.
Множество, состоящее из элементов, входящих хотя бы в одно из множеств А или В, называются объединением множеств А и В и обозначается А В.
Множество, состоящее из элементов, входящих в оба множества А и В, называются пересечением множеств А и В и обозначается А В.
Множество, состоящее из элементов, входящих в А, но не входящих в В, называется разностью множеств А и В и обозначается А\В.
Если
имеется некоторое универсальное множеств
V
такое, что все рассматриваемые множества
являются его подмножествами, то может
быть введена операция дополнения
![]()
Операции над множествами могут быть наглядно представлены с помощью диаграмм Эйлера-Венна:
V
ФА V V
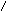
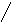
















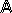




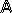
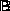

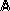
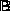
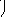



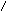
![]()
![]()
![]()
1.3. Свойства операций
Операции
![]() производимые над подмножествами
некоторого множестваV,
обладают следующими свойствами:
производимые над подмножествами
некоторого множестваV,
обладают следующими свойствами:
A A=A, AA=A -идемпотентность
AB=BA, AB=BA -коммутативность
(AB) C=A (B C),
(AB) C=A(BC) -ассоциативность
A(AB)=A, A (AB)=A -поглощение
A(BC)=(AB)(AC),
A(BC)=(AB) (AC) -дистрибутивность
A
 =,
A=
A=A
-закон
нуля
=,
A=
A=A
-закон
нуляA
 =V,
AV=V,
AV=A
-закон
единицы
=V,
AV=V,
AV=A
-закон
единицы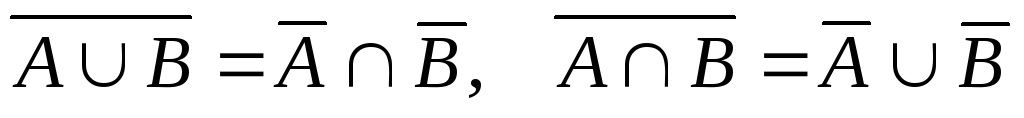 -правило де
Моргана
-правило де
Моргана =A
-инволютивность.
=A
-инволютивность.
Заметим, что система свойств не изменяется, если одновременно поменять местами операции и и множества и V. Это есть проявление так называемого принципа двойственности.
Любая структура с 3
операциями, обладающими перечисленными
свойствами, называется булевой алгеброй.
Множество подмножеств множества Vс операциями![]() образует,
следовательно, булеву алгебру.
образует,
следовательно, булеву алгебру.
Отметим,
что, если
![]() - конечноеn
– элементное множество, то любое его
подмножество
- конечноеn
– элементное множество, то любое его
подмножество
![]() может быть задано с помощью двоичного
набора
может быть задано с помощью двоичного
набора
![]() .
.
При
этом
![]() означает, что
означает, что![]() Набор
Набор![]() называется характеристическим вектором
множестваА.
называется характеристическим вектором
множестваА.
1.4. Мощность множества.
Мощность
конечного множества – это число его
элементов, обозначается
![]() .
Если
.
Если![]() ,
то
,
то![]() .
Бесконечные множества считаются
равномощными, если между их элементами
может быть установлено взаимно однозначное
соответствие. Определенная таким образом
мощность называется также кардинальным
числом. Если элементы множества могут
быть поставлены во взаимно однозначное
соответствие с членами натурального
ряда, то говорят, что оно счетно. Множество
рациональных чисел счетно.
.
Бесконечные множества считаются
равномощными, если между их элементами
может быть установлено взаимно однозначное
соответствие. Определенная таким образом
мощность называется также кардинальным
числом. Если элементы множества могут
быть поставлены во взаимно однозначное
соответствие с членами натурального
ряда, то говорят, что оно счетно. Множество
рациональных чисел счетно.
Для
бесконечных множеств мощности множества
и его собственного подмножества могут
совпадать, что в определенной степени
нарушает привычные представления. Так
множество натуральных чисел {1,2,3,
...} и множество
квадратов натуральных чисел {1,4,9,...}
имеют
одинаковую мощность. Оба они счетны,
что доказывается установлением между
их элементами взаимно однозначного
соответствия по правилу
![]() ,
но второе из множеств является
подмножеством первого.
,
но второе из множеств является
подмножеством первого.
Множество действительных чисел не может быть поставлено во взаимно однозначное соответствие с натуральным рядом, поэтому оно имеет большую мощность, которая называется континуум. Множество действительных чисел, принадлежащих отрезку [a;b] или интервалу (a;b) при a<b также имеет мощность континуум.
Докажем,
что множество действительных чисел из
интервала (0;1)
не является
счетным, с помощью диагонального метода
Кантора. Допустим противное, что это
множество счетное. Тогда все числа из
(0;1)могут
быть выписаны в виде последовательности
![]() .
Каждое из этих чисел можно представить
в виде бесконечной десятичной дроби
.
Каждое из этих чисел можно представить
в виде бесконечной десятичной дроби
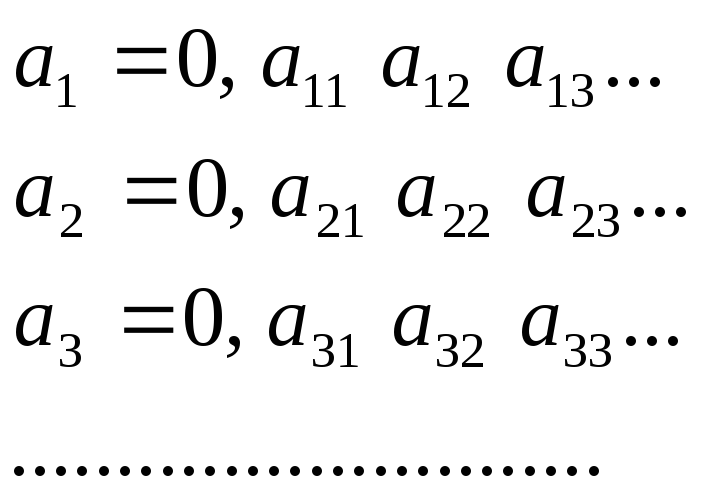
Выпишем
теперь число
![]() ,
руководствуясь следующим правилом:b1
- любая десятичная цифра, не равная a11;
b2-
любая цифра, не равная a22;
b3
- не равная a33
и т.д. Тогда
,
руководствуясь следующим правилом:b1
- любая десятичная цифра, не равная a11;
b2-
любая цифра, не равная a22;
b3
- не равная a33
и т.д. Тогда
![]() ,
но числаb
нет в выписанной последовательности.
Полученное противоречие и доказывает
несчетность множества действительных
чисел из интервала (0;1)
,
но числаb
нет в выписанной последовательности.
Полученное противоречие и доказывает
несчетность множества действительных
чисел из интервала (0;1)
