
- •Министерство образования российской федерации
- •Содержание.
- •Глава I. Множества.
- •1.1. Определения и обозначения.
- •1.2. Операции над множествами.
- •1.3. Свойства операций
- •1.4. Мощность множества.
- •1.5. Прямое произведение множеств.
- •Глава II. Отношения, функции, алгебраические
- •2.1. Бинарные отношения.
- •2.2. Функции.
- •2.3. Алгебраические структуры и морфизмы.
- •Отношение конгруэнтности позволяет определить так называемую фактор-структуру, носителем которой является множество классов эквивалентности. Приведём примеры.
- •Контрольные вопросы
- •Тест II
- •Глава III. Булевы функции.
- •3.1. Определение и основные свойства.
- •3.2 Дизъюнктивная и конъюнктивная нормальные формы
- •3.3. Упрощение д.Н.Ф.
- •Контрольные вопросы.
- •Тест III
- •Глава IV. Элементы математической логики
- •4.1. Исчисление высказываний.
- •4.2. Логическое следствие
- •4.3. Предикаты и кванторы
- •Тест IV.
- •Глава 5. Алгоритмы и машина Тьюринга.
- •5.3. Машина Тьюринга.
- •F : q a a
- •5.4. Алгоритмически неразрешимые проблемы.
- •Итоговый тест.
- •Рекомендуемая литература. Основная:
- •Дополнительная
- •Словарь основных терминов
- •Ответы к тестам
- •Зуев Юрий Анатольевич Садыкова Альбина Рифовна Математическая логика и теория алгоритмов. Теория множеств. Дискретная математика
1.5. Прямое произведение множеств.
Прямым
(или декартовым) произведением множеств
А
и В
называется множество
![]() ,
состоящее из всех упорядоченных пар(a,b)
таких, что
,
состоящее из всех упорядоченных пар(a,b)
таких, что
![]() и
и![]() .
.
Если А иВ- конечное
множество, мощности![]() и
и![]() ,
то
,
то![]() .
.
Геометрическим
образом множества действительных чисел
Rявляется прямая, а геометрическим
образом декартового квадрата![]() является плоскость.
является плоскость.
Множество всех двоичных наборов длины
nможно рассматривать как![]() -n-ую декартову степень двухэлементного
множества
-n-ую декартову степень двухэлементного
множества![]() .
Отсюда следует, что число двоичных
наборов длиныnравно2n.
Считая каждый двоичный набор
характеристическим вектором подмножестваn-элементного множества, получаем,
что число всех подмножествn-элементного
множества равно2n.Этим объясняется часто используемое
обозначение2Aдля множества
всех подмножествA, которое
используется как для конечных, так и
для бесконечных множеств.
.
Отсюда следует, что число двоичных
наборов длиныnравно2n.
Считая каждый двоичный набор
характеристическим вектором подмножестваn-элементного множества, получаем,
что число всех подмножествn-элементного
множества равно2n.Этим объясняется часто используемое
обозначение2Aдля множества
всех подмножествA, которое
используется как для конечных, так и
для бесконечных множеств.
Если
A
конечное непустое множество,
![]() ,
то
,
то![]() ,
так как2n>n
при
,
так как2n>n
при
![]() Покажем, что для бесконечных множеств
данное соотношение между мощностями
сохраняется. Допустим противное, пусть
междуA
и 2A
установлено взаимно однозначное
соответствие
Покажем, что для бесконечных множеств
данное соотношение между мощностями
сохраняется. Допустим противное, пусть
междуA
и 2A
установлено взаимно однозначное
соответствие
![]() .
Определим множество
.
Определим множество![]()
![]() следующим образом. Для каждого
следующим образом. Для каждого![]() включимa
в B
в том и только в том случае, если
включимa
в B
в том и только в том случае, если
![]() .
Пусть
.
Пусть![]() ,
гдеb-элементы
множества A
, для которого
,
гдеb-элементы
множества A
, для которого
![]() .
Зададимся теперь вопросом, является лиb
элементом множества B?
Если
.
Зададимся теперь вопросом, является лиb
элементом множества B?
Если
![]() ,
то
,
то![]() по построению множестваB.
А если
по построению множестваB.
А если
![]() ,
то
,
то![]() опять таки по построению множестваB.
Таким образом, одновременно имеет место
опять таки по построению множестваB.
Таким образом, одновременно имеет место
![]() и
и![]() .
Полученное противоречие и доказывает
невозможность установления взаимно
однозначного соответствия междуA
и 2A.
.
Полученное противоречие и доказывает
невозможность установления взаимно
однозначного соответствия междуA
и 2A.
Контрольные вопросы.
Что называется множеством?
Дайте определение пересечения множеств.
Что называют мощностью множества?
Дайте определение прямого произведения множеств.
Приведите примеры множества.
Тест 1.
Объединением множеств А и В называется множество…
а)![]() {
{![]() или
или![]() };
б) {
};
б) {![]() и
и![]() };
};
в)
{![]() и
и![]() };
в) {
};
в) {![]() и
и![]() };
};
2.
Какая операция над множествами А, В, и
С изображена на диаграмме![]()


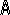











а)
![]() ;
б)
;
б)![]() ;
в)
;
в)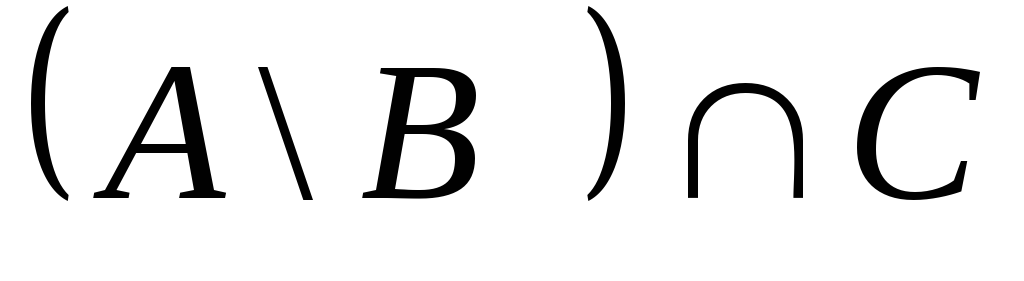 ;
г)
;
г)![]() ;
;
Даны множества
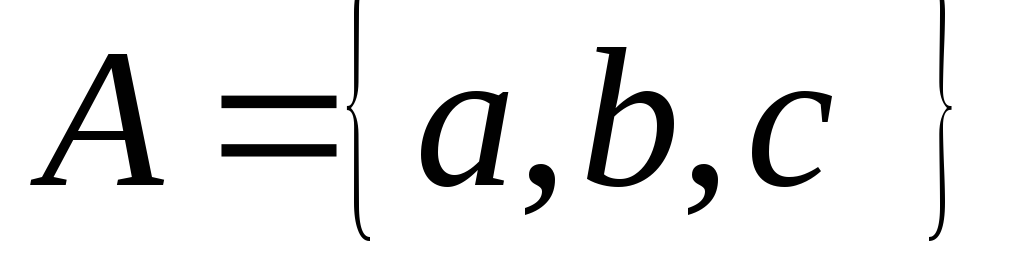 ,
,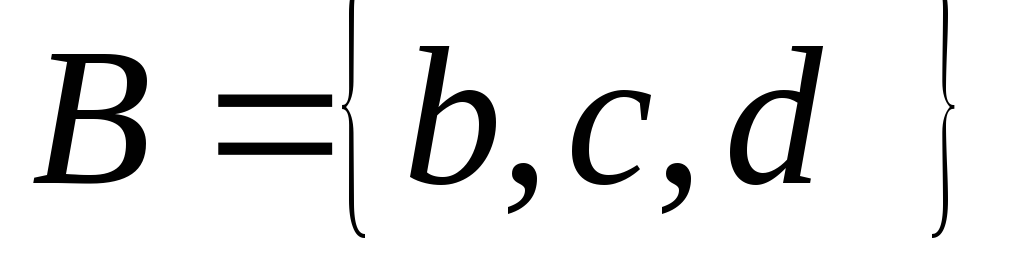 и
и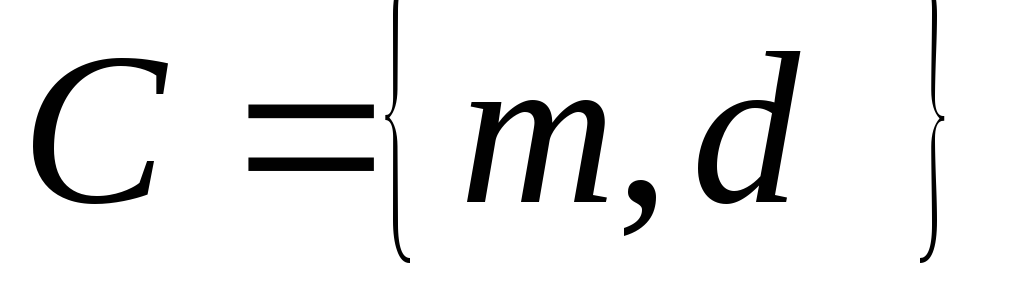 .
Результатом операции (А\В)
.
Результатом операции (А\В) С
будет множество:
С
будет множество:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г){Ø}.
;
г){Ø}.
А={1, 2, 3}, В={а, в}. Какая пара чисел не принадлежит декартовому произведению А
 B
B
а) (1, а); б) (2, в); в) (3, а); г) (а, 2).
Является ли множество целых чисел счётным?
а) да; б) нет.
Глава II. Отношения, функции, алгебраические
структуры, морфизмы.
2.1. Бинарные отношения.
Пусть A- множество. Если задано некоторое
подмножество![]() его декартового квадрата, другими
словами, задано некоторое подмножество
упорядоченных пар
его декартового квадрата, другими
словами, задано некоторое подмножество
упорядоченных пар![]() ,
где
,
где![]() ,
то говорят, что на множествеAзадано бинарное отношениеR.
Пишут
,
то говорят, что на множествеAзадано бинарное отношениеR.
Пишут![]() или
или![]() .В
качестве примеров бинарных отношений
на числовых множествах можно рассмотреть
хорошо известные из арифметики отношения:
,,=”, ,,<”, ,,”,
,,>”, ,,”.
.В
качестве примеров бинарных отношений
на числовых множествах можно рассмотреть
хорошо известные из арифметики отношения:
,,=”, ,,<”, ,,”,
,,>”, ,,”.
Бинарное отношение называется:
-
рефлексивным, если для любого
![]()
-
иррефлексивным, если для любого
![]() ;
;
-
симметричным, если из
![]() следует
следует![]() ;
;
-
антисимметричным, если
![]() и
и![]() следуетa=b;
следуетa=b;
-
транзитивным, если из
![]() и
и![]() следует
следует![]() ;
;
Отношение ,,=” рефлексивно, симметрично и транзитивное, отношения ,,<” и ,,>” транзитивны и иррефлексивны, отношения ,,” и ,,”. рефлексивны, антисимметричны и транзитивны. Последние свойства выбираются в качестве определяющих для отношения частичного порядка на множестве A.
Определение. Бинарное отношение R на множестве A называется отношением частичного порядка, если оно рефлексивно, антисимметрично и транзитивно,
Если
![]() ,
то будем считать элементa
предшествующим элементу b
и записывать отношение aRb
в виде
,
то будем считать элементa
предшествующим элементу b
и записывать отношение aRb
в виде
![]() .
Если для любых двух
.
Если для любых двух![]() элементов имеет место хотя бы одно из
отношений
элементов имеет место хотя бы одно из
отношений![]() или
или![]() ,
то частичный порядок называется полным
или линейным порядком.
,
то частичный порядок называется полным
или линейным порядком.
Примером
частичного порядка является система
множеств, упорядоченных по включению:
![]() .
Числовые множества с обычным отношением
,,”
дают примеры линейных порядков.
.
Числовые множества с обычным отношением
,,”
дают примеры линейных порядков.
Пусть
<A,
> - частично
упорядоченное множество. Элемент
![]() называется минимальным, если из
называется минимальным, если из![]() следует
следует![]() .
Минимальных элементов может быть больше
одного. Элемент
.
Минимальных элементов может быть больше
одного. Элемент![]() называется наименьшим, если
называется наименьшим, если![]() для любого
для любого![]() .
Если вA
имеется наименьший элемент, то он
единственен. Аналогично определяются
максимальный и наибольший элемент.
.
Если вA
имеется наименьший элемент, то он
единственен. Аналогично определяются
максимальный и наибольший элемент.
Обобщением понятия равенства является отношение эквивалентности.
Определение. Бинарное отношение R на множестве A называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Отношение
эквивалентности разбивает множество
Aна непересекающиеся
подмножества, называемые классами
эквивалентности. Если в качествеAрассмотреть множество людей, проживающих
в домах некоторого города, то отношение
проживания в одном доме будет отношением
эквивалентности. Более математическим
примером является отношение сравнения
по модулюnв множестве
целых чиселZ:
![]() ,
если
,
если![]() делится наn. При этомZразбивается на
классы
делится наn. При этомZразбивается на
классы![]() ,
характеризуемые остатками от деления
наn. Более общим
примером является эквивалентность
элементов группыGпо подгруппеH:
,
характеризуемые остатками от деления
наn. Более общим
примером является эквивалентность
элементов группыGпо подгруппеH:![]() если
если![]() .
Классами эквивалентности здесь являются
правые смежные классы по подгруппеH.
.
Классами эквивалентности здесь являются
правые смежные классы по подгруппеH.
