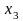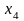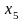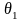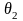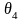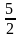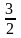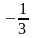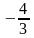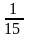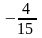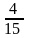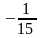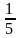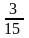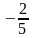министерство образование и науки

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ

Кафедра высшей математики

А.А.Копанева, Е.Н.Родионова

МАТЕМАТИКА

Учебно-практическое пособие для студентов экономических специальностей дневной формы обучения

Москва, 2010 г.

УДК

 А.А.Копанева, Е.Н.Родионова Математика.- М.: МГУТУ, 2010.

Данное учебно-практическое пособие включает решения задач для самостоятельной работы студентов экономических специальностей второго курса четвертого семестра дневной формы обучения. Содержит теоретические сведения, разобранные примеры и список рекомендуемой литературы. Может быть использовано для студентов всех форм обучения и аспирантов, а также исследователей в различных областях науки, применяющими математические методы при решении экономических задач.

Авторы: А.А.Копанева, Е.Н.Родионова

Рецензент: д.ф.-м.н., Зуев Ю.А.

Московский государственный университет технологий и управления, 2010

109004, Москва, Земляной вал, 73

Содержание

А.А.Копанева, Е.Н.Родионова 1

МАТЕМАТИКА 1

 А.А.Копанева, Е.Н.Родионова Математика.- М.: МГУТУ, 2010. 2

1. Балансовая модель Леонтьева 4

2. Линейное программирование 6

3. Транспортная задача линейного программирования 16

4. Модели динамического программирования. Задача распределения капиталовложений 20

5. Теория игр. 27

1. Балансовая модель Леонтьева 4

2. Линейное программирование 6

3. Транспортная задача линейного программирования 15

4. Модели динамического программирования. Задача распределения капиталовложений 19

5. Теория игр. 27

1. Балансовая модель Леонтьева

Используя балансовый метод планирования и модель Леонтьева, построить баланс производства и распределения продукции предприятий.

Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции первого вида, второе предприятие – продукции второго вида, третье предприятие – продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям, является конечным продуктом). Специалистами управляющей компании получены экономические оценки 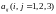элементов технологической матрицы A (норм расхода, коэффициентов прямых затрат) и элементов y_i вектора конечной продукции Y.

Предприятия (виды продукции)	Коэффициенты прямых затрат			Конечный продукт Y
	I	II	III
I	0,1	0,12	0,125	100
II	0,05	0,04	0,075	200
III	0,3	0,12	0,025	300

По этим данным построить баланс производства и распределения продукции предприятий холдинга. Для определения матрицы полных затрат использовать итерационный метод, ограничившись четырьмя членами разложения.

Решение. В условии задачи

; .

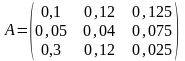Матрица полных затрат приближенно равна

.

Пользуясь полученной матрицей полных затрат, вычислим объемы валовой продукции рассматриваемых предприятий пр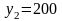и , и как произведение матрицы полных затрат B на матрицу-столбец конечной продукции Y:

.

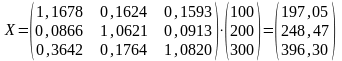Межотраслевые поставки определим по формуле , :

; ; ;

; ; ; ; ; .

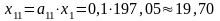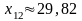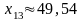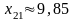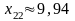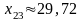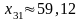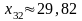Заполним схему баланса производства и распределения продукции предприятий холдинга

Производящие предприятия (виды продукции)	Потребляющие предприятия			Конечный продукт	Валовый выпуск
	I	II	III
I	19,70	29,82	49,54	100	197,05
II	9,85	9,94	29,72	200	248,47
III	59,12	29,82	9,91	300	396,30

2. Линейное программирование

Решить задачу линейного программирования:

а) вычислить значения целевой функции в точках области допустимых решений (ОДР), имеющих целочисленные координаты;

б) графическим методом;

в) методом перебора опорных решений;

г) симплекс-методом;

д) составить двойственную задачу и на основании теорем двойственности, сделать вывод о ее решении.

ОДР:

Решение.

а) вычислим значения целевой функции в точках области допустимых решений (ОДР), имеющих целочисленные координаты.

F(2,3)=4+3=7- min, F(3,4)=6+4=10, F(4,5)=8+5=13, F(5,6)=10+6=16

F(6,7)=12+7=19, F(4,4)=8+4=12, F(5,4)=10+4=14, F(5,5)=10+5=15

F(6,4)=12+4=16, F(6,5)=12+5=17, F(6,6)=12+6=18, F(6,7)=12+7=19

F(7,8)=14+8=22-max.

б) графический метод.

Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в случае, если:

1) система ограничений состоит из неравенств с двумя переменным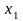и и ;

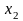2) система ограничений состоит из 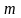уравнений с 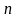переменными и .

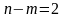И в том и в другом случае система ограничений определяет на плоскости (в пространстве) выпуклый многоугольник (многогранник). Он определяет область допустимых решений. Оптимальное решение задачи, если оно существует, находится среди множества вершин многоугольника (многогранника) решений системы ограничений.

Алгоритм графического метода решения задач линейного программирования с двумя переменными:

1. Построить область допустимых решений.

2. Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.

3. Если область допустимых решений является непустым множеством, построить нормаль к опорной прямой (L).

4. Опорную прямую в задаче на максимум перемещать в направлении вектора нормали, в задаче на минимум – в противоположном направлении.

5. Определить координаты экстремальных точек (пересечение опорных прямых с ОДР). Если целевая функция задачи параллельна одной из прямых ограничений, то задача имеет бесконечное множество решений.

6. После нахождения оптимальных решений вычисляется значение целевой функции на этих решениях.

Рис. 2.1

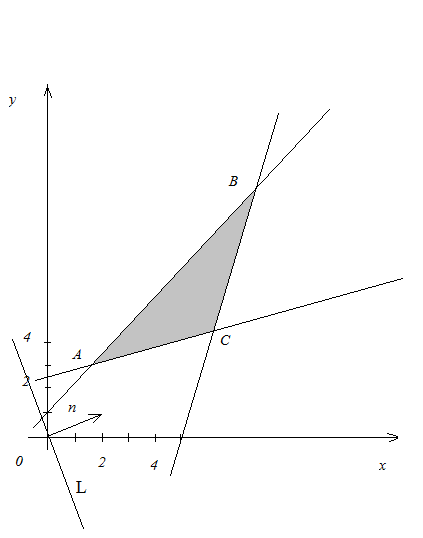
По системе ограничений построим многоугольник, который определит область допустимых решений. Координаты вершин многоугольника допустимых решений определяют опорные решения.

Построим прямые, которые задают ОДР.

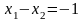- прямая АВ.

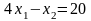- прямая ВС.

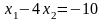- прямая АС.

По целевой функции 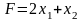построим вектор 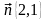и опорную прямую 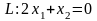, перпендикулярную вектору .

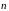Найдем оптимальный план, то есть те значения и , при которых F принимает максимальное значение.

При перемещении прямой L в направлении вектора 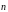значение F увеличивается. Крайняя вершина многоугольника решений (точка “выхода”), в которой значение F будет максимальным - точка B ( , ). Точка B( , ) лежит на пересечении прямых (1) и (2), заданных уравнениями и .

Решая систему 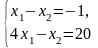, найдем значения: = 7; = 8.

При этих значениях х₁ и х₂ значение функции F будет максимальным.

Чтобы найти минимальное значение функции F будем перемещать прямую L в направлении, противоположном направлению вектора . Точка А( , ) – точка, в которой значение F – минимально. Она лежит на пересечении прямых (1) и (3), координаты которой находим аналогично, решая систему из двух уравнений. Получим = 2, = 3, .

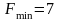в) метод перебора опорных решений.

Приведем задачу линейного программирования к каноническому виду.

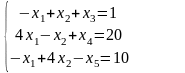
Исходные данные запишем в виде таблицы. В правой части таблицы на каждом шаге вычислений приведены значения параметра 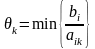, минимальное значение которого выделено жирным шрифтом, где -это свободный член в системе ограничений, а 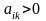- коэффициенты при соответствующих переменных. С помощью данного условия можно выбрать разрешающий элемент (клетка с разрешающим элементом выделена) в любом столбце k матрицы системы ограничений, в котором имеется хотя бы один положительный элемент. Если при выборе разрешающего элемента данное условие нарушается, в правой части системы уравнений появляются отрицательные величины. При переходе от одного опорного решения к другому используется аналогичное условие.

Таблица 2.1

-1	1	1	0	0	1	-	1	1	-	-
4	-1	0	1	0	20	5	-	-	20	-
1	-4	0	0	1	-10	-		-	-	-

Базис 3,4,5.

-1	1	1	0	0	1	-	1	1	-	-
3	0	1	1	0	21	7	-	21	21	-
-3	0	4	0	1	-6	-	-		-	-

Базис 2,4,5.

0	1			0	8	-	8	6	24	-
1	0			0	7	7	-	9	21	-
0	0	5	1	1	15	-	-	3	15	15

Базис 1,2,5. При F=14+8=22- max.

0	1		0		3	-	3	-	-	-
1	0		0		2	2	-	-	-	-
0	0	5	1	1	15	-	-	3	15	15

Базис 1,2,4. При 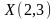F=4+3=7 - min.

Из базиса 1,2,5, возможен переход в базис 1,2,3, если выбрать другой разрешающий элемент.

0	1			0	8	-	8	6	24	-
1	0			0	7	7	-	9	21	-
0	0	5	1	1	15	-	-	3	15	15

0	1	0			4	-	4	-	60	-
1	0	0			6	6	-	-	22,5	-
0	0	1			3	-	-	3	15	15

Из полученных опорных решений выбираются те, в которых целевая функция принимает максимальное и минимальное значение. Других базисных решений нет.

г) симплекс-метод.

Оптимальное решение задачи линейного программирования можно найти путем перебора не всех, а только части опорных решений. Для этого необходимо каждое опорное решение проверять на оптимальность и переход от одного опорного решения к другому осуществлять так, чтобы значение целевой функции увеличивалось в задаче на максимум или уменьшалось в задаче на минимум.

Решим данную задачу симплекс-методом на минимум.

_{Так как опорные решения были найдены в пункте в), то за основу возьмем одно из найденных решений.}

После того как исходное опорное решение получено, заполним симплекс-таблицу.

0	1			0	8
1	0			0	7
0	0	5	1	1	15
0	0	2	1	0	22

Четвертая строка в таблицы - индексная, в ней записаны соответствующие коэффициенты целевой функции.

Проверим, признак оптимальности: если все элементы индексной строки (строки целевой функции) неположительны (неотрицательны), то полученный план – минимальный (максимальный), то есть оптимальный (план при котором достигается наибольшее или наименьшее значение функции).

Разрешающий столбец определяется исходя из коэффициентов целевой функции и соответствует отрицательному значению коэффициента (в задаче на максимум) и положительному значению коэффициента (в задаче на минимум).

Для определения разрешающей строки вычисляется отношение элементов столбца свободных членов на соответствующие элементы разрешающего столбца. Разрешающей строке будет соответствовать минимальный положительный результат такого деления.

В данном случае в столбце, соответствующем свободной переменной , у целевой функции есть положительный элемент 2, следовательно, признак оптимальности нарушен и план, соответствующий полученному опорному решению можно улучшить.

Выбираем разрешающий элемент, который расположен на пересечении разрешающего столбца и разрешающей строки. В рассматриваемом примере разрешающий элемент 5.

Все элементы таблицы пересчитываются по методу Жордана-Гаусса.

Получим таблицу.

0	1	0			4
0	0	1			6
1	0	0			3
0	0	0			16

0	1		0		3
1	0		0		2
0	0	5	1	1	15
0	0	-3	0	-1	7

Из последней симплекс таблицы видно, что в индексной строке нет положительных элементов при решении задачи на минимум целевой функции, поэтому достигнуто оптимальное решение.

Минимальное значение функции F=7 при .

д) составить двойственную задачу и на основании теорем двойственности, сделать вывод о ее решении.

Правила составления двойственных задач:

1. Во всех ограничениях исходной задачи свободные члены должны находится в правой части, а члены с неизвестными – в левой.

2. Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.

3. Если знаки неравенств в ограничениях исходной задачи « », то целевая функция должна максимизироваться, а если « » - минимизироваться.

4. Каждому ограничению исходной задачи соответствует неизвестное в двойственной; при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-равенству, может быть любого знака.

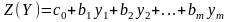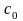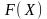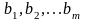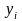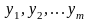5. Целевая функция двойственной задачи имеет вид , где -свободный член целевой функции исходной задачи, - свободные члены в ограничениях исходной задачи, при этом - свободный член именно того ограничения исходной задачи, которому соответствует неизвестная , а - неизвестные в двойственной задаче.

6. Целевая функция 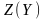двойственной задачи должна оптимизироваться противоположным по сравнению с образом.

7. Каждому неизвестному исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих ограничений (вместе с условиями неотрицательности неизвестных ) образует систему ограничений двойственной задачи. Все ограничения имеют вид неравенств, а знаки имеют вид « », ес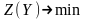ли и « », если .

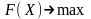Прямая задача:

Двойственная данной:

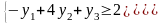
Из последней симплекс-таблицы решения прямой задачи (пункт г)), выписываем решение двойственной. Для этого согласно второй теореме двойственности устанавливаем соответствие между переменными прямой и двойственной задач. Получим 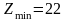при при _.
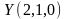