37. Уравнения прямой в пространстве. Расстояние от точки до плоскости в пространстве

Общее уравнение прямой в пространстве рассматривается как линия пересечения двух плоскостей

L:

Канонические уравнения прямой в прострнанстве.

Пусть дан отличный от нуля вектор S(l,m,n)- направляющий вектор прямой L и точка M₀(x­₀, y­₀,z₀) принадлежит L. М(x,y,z)

M­₀M|| S => M₀M=kS=> x-x₀\l=y-y₀\m=z-z₀\n

Параметрические уравнения прямой

x=x₀+kl

y=y₀+km

z=z₀+kn

Уравнение прямой, проходящей через 2 точки M₁,M₂

M₁(x₁,y₁,z₁) M₂(x₂,y₂,z₂)

L:

Если ни одно из значений в знаменателе не равно нулю

Если прямая L перпендикулярна нормалям двух плоскостей, то за направление S прямой L можно принять векторное произведение нормалей n₁ и n₂

S=n₁xn₂=

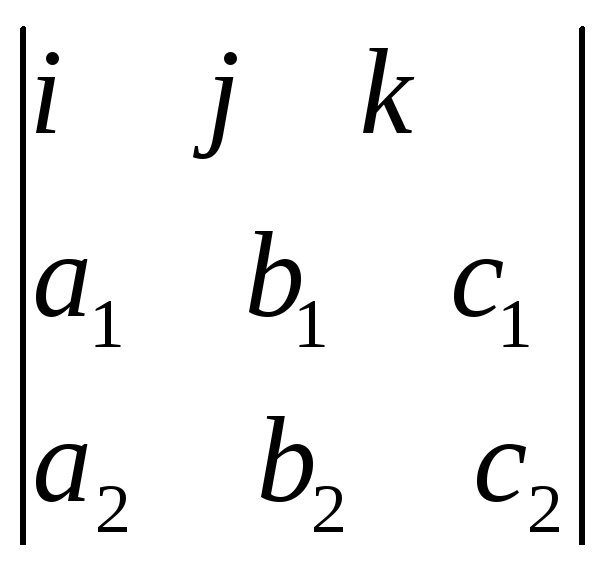
алгоритм для нахождения расстояния от точки до плоскости альфа следующий:

составляем уравнение прямой a, которая проходит через точку М1 и перпендикулярна к плоскости альфа;

находим координаты (x₂,y₂,z₂) точки H1 - точки пересечения прямой a и плоскости  альфа;

вычисляем расстояние от точки М1 до плоскости альфа по формуле .

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Если s = {m; n; p} - направляющий вектор прямой L, M1(x1, y1, z1) - точка лежащей на прямой, тогда расстояние от точки M0(x0, y0, z0) до прямой l можно найти, используя формулу

Условие перпендикулярности прямых

или в коорд. Форме l₁l₂+m₁m₂+n₁n₂=0

Условие параллельности прямых

L₁||L₂S₁||S₂S₁=k*S₂

38. Параметрическое задание прямой. Пересечение прямой и плоскости

Пусть дан отличный от нуля вектор S(l,m,n)- направляющий вектор прямой L и точка M₀(x­₀, y­₀,z₀) принадлежит L. М(x,y,z)

M­₀M|| S => M₀M=kS=> x-x₀\l=y-y₀\m=z-z₀\n =t

  В координатах (параметрические уравнения):

Пересечение прямой и плоскости.

Пусть требуется найти точки пересечения прямой с плоскостью. Для этого надо решить систему уравнений

Если , то

L:x-x₀\l=y-y₀\m=z-z₀\n =t

Подставляя значения параметрических уравнений прямых в уравнение плоскости получим

a(x₀+tl)+b(y₀+tm)+c(z₀+tn)+d=0

Отсюда находим t, подставляем в параметрические уравнения и получаем ответ

Если L не перпендикулярна, то , тогда

Отсюда находим t, подставляем в параметрические уравнения и получаем ответ

Если n*S=0, то есть L||, то пересечения не будет

Вопрос 39. (Уравнение окружности).

Уравнение окружности ω (A; R) имеет вид (x – a)² + (y – b)² = R², где a и b – координаты центра A окружности ω (A; R) .

Вопрос 40. (Эллипс, уравнения и свойства).

Эллипс – геометрическое место точек на плоскости, сумма расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная.

Коническое уравнение эллипса:

Эксцентриситет эллипса – отношение фокального расстояния к длине большой от эллипса.

Вопрос 41. (Гипербола, уравнение и свойства).

Гипербола – геометрическое место точек на плоскости, разность расстояний каждой из которых до двух разных точек, называется фокусами, есть величина постоянная.

Каноническое уравнение гиперболы:

Вопрос 40. (Эллипс, уравнения и свойства).

Эллипс – геометрическое место точек на плоскости, сумма расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная.

Коническое уравнение эллипса:

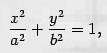
Эксцентриситет эллипса – отношение фокального расстояния к длине большой от эллипса.

Вопрос 41. (Гипербола, уравнение и свойства).

Гипербола – геометрическое место точек на плоскости, разность расстояний каждой из которых до двух разных точек, называется фокусами, есть величина постоянная.

Каноническое уравнение гиперболы:

Вопрос 42. (Парабола, уравнение и свойства).

Парабола – геометрическое место точек на плоскости, равноудалённых от данной точки называемой фокусами данной прямой, называется директрисой.

Каноническое уравнение параболы: y² = 2px ?

Эксцентриситет параболы. По определению …

Свойства параболы:

1)       Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2)       Вся парабола расположена в правой полуплоскости плоскости Оху.