Кто открыл этот документ – тот педик ;) Экзамен по математике. I семестр.

Тема 1. Матрицы и определители. Решение и исследование систем линейных алгебраических уравнений

1. Матрица. Различные виды матриц.

Матрицей размера или порядка mn называется прямоугольная таблица чисел, имеющая m строк и n столбцов.

Виды:

Матрица называется квадратной, если m=n.

Квадратная матрица, у которой все элементы, стоящие вне главной диагонали, равны нулю, называется диагональной.

Квадратная матрица, у которой все элементы выше или ниже главной диагонали равны 0, называется треугольной.

Если в прямоугольной матрице элементы, стоящие ниже главной диагонали, равны 0, то матрица называется трапециевидной.

Матрица называется транспортированной, если строки поменять на соответствующие столбцы.

Если в диагональной матрице все элементы, стоящие на главной диагонали равны 1, то матрица называется единичной.

Матрица, состоящая из 0, называется нулевой матрицей.

Квадратная матрица называется вырожденной, если определитель этой матрицы равен 0.

Квадратная матрица называется невырожденной, если определитель этой матрицы не равен 0.

2. Сумма, разность и умножение матриц. Свойства сложения и умножения матриц.

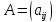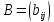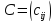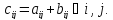Суммой матриц  и одинаковых размеров называется матрицатех же размеров, у которойОбозначение:C = А + В.

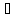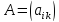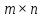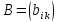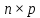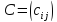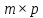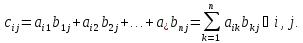Свойства сложения матриц: А + В = В + А, (А + В) + С = A + (B + C), А + 0 = A, А + (-A) = 0, A, B, C. Вычитание матриц: А - В = А + (-В). Произведением матрицыразмеромна матрицуразмеромназывается матрицаразмерому которойОбозначение:C = AB.

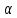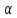Свойства AE = EA = A, AO = OA = O, (AB)D = A(BD), (AB) = (A)B = A(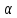B), (A + B)D=AD + BD, D(A + B) = DA + DB (при условии, что указанные операции имеют смысл).

Для квадратных матриц А и B, вообще говоря,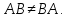 

3. Определители второго и третьего порядков, их свойства.

Определителем второго порядка называется число равное произведению элементов стоящих на главной диагонали минус произведение элементов стоящих на побочной диагонали.

Определителем третьего порядка называется число равное

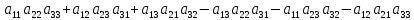
и обозначаемое символом

Итак, по определению

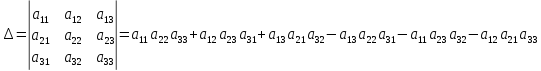
Свойства.

1. Транспонированный определитель равен данному.

2. Определитель, имеющий две одинаковые строки (столбца) равен нулю.

3. Постоянный множитель строки или столбца можно выносить за знак определителя.

4. Определитель, имеющий 2 пропорциональные строки или столбца равен 0.

5. Определитель, имеющий строку (столбец) состоящей из нулей равен 0.

6. Если в определителе поменять местами 2 соседние строки (столбца), то это равносильно умножению определителя на -1.

7. Величина определителя не изменится, если к элементам какой либо строки (столбца) прибавить элементы другой строки (столбца), умноженное на некоторое число.

8. Сумма произведений элементов какой либо строки или столбца на алгебраические дополнения другой строки или столбца равно 0.

4. Алгебраические дополнения и миноры. Понятие об определителе n-го порядка.

Алгебраическим дополнением какого либо элемента называется минор этого элемента, взятый со знаком +, если сумма номеров строки и столбца, на пересечении которых находится этот элемент число чётное и со знаком -, если нечётное.

Минором какого либо элемента определителя называется определитель, полученный из данного путём вычёркивания той строки и того столбца, на пересечении которых находится этот элемент.

Определителем или детерминантом n-го порядка называется число записываемое в виде

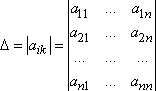
5. Обратная матрица. Способ нахождения обратной матрицы.

Матрица A ^{− 1} называется обратной к квадратной матрице A n –го порядка, если A · A ^{− 1} = A ^{− 1} · A = E, где E — единичная матрица n –ого порядка.

Способ нахождения обратной матрицы.

1)Сначала проверим является ли А квадратной, т.е. совпадают ли n и k.

2)Затем проверим равен ли определитель мартицы А нулю. Если он равен нулю, то обратной матрицы не существует.

3)С помощью матрицы алгебраических дополнений

—транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

6. Матричная запись системы линейных уравнений и решение системы в матричной форме.

Матричная запись системы линейных уравнений , где  — основная матрица системы, и  — столбцы свободных членов и решений системы соответственно:

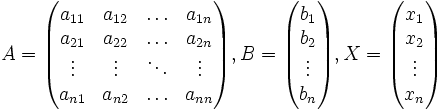
Решение системы в матричной форме. Первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A^-1, получим A^-1AX= A^-1B, откуда EX=X=A^-1B. Следовательно, матрица-решение X легко находится как произведение A^-1 и B.

7. Система трёх линейных уравнений с тремя неизвестными. Правило Крамера.

Система трех линейных уравнений с тремя неизвестными имеет вид

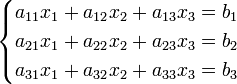
Правило Крамера.

Дана система линейных уравнений:

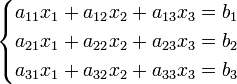
Определители:

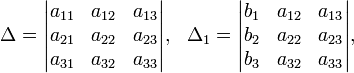
Решение:

8. Решение систем линейных алгебраических уравнений методом Гаусса.

Метод Гаусса состоит в последовательном исключении неизвестных (то есть приведение матрицы к треугольному или трапециевидному виду).

9. Ранг матрицы, его вычисление. Теорема Кронекера-Капелли.

Ранг матрицы, его вычисление. Одним из способов вычисления ранга матрицы является метод окаймления миноров.

Другой способ вычисления ранга матрицы основан на применении элементарных преобразований матрицы и использовании следующих утверждений.

1) Ранг ступенчатой матрицы равен количеству её ненулевых строк.

2) Элементарные преобразования матрицы не изменяют её ранг.

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

10. Исследование решений систем линейных алгебраических уравнений.

1. Δ ≠0 система имеет единственное решение

2. Δ=0, а хотя бы один из вспомогательных ≠0, то решений нет

3. Δ= Δ1= Δ2= Δ3=0 бесчисленное множество решений