
Тема 4. Введение в математический анализ
Числовая последовательность и ее предел.
Функция, областью определения которой является множество натуральных чисел называется последовтельностью.
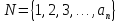
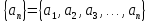
Если
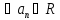 то последовательность называется
числовой.
то последовательность называется
числовой.
Число
А называется пределом числовой
последовательности
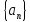 ,
если
,
если можно указать
можно указать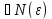 ,
что для всех членов этой последовательности
,
что для всех членов этой последовательности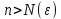 выполняется неравенство
выполняется неравенство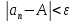
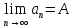
Определение функции. Способы задания функции.
Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х - независимая переменная или аргумент и переменная у - зависимая переменная.
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Обратная функция. Сложная функция.
Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией.
Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
Определение предела функции в точке на языке «
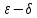 ».
Понятие односторонних пределов.
Формулировка теоремыo
существовании предела функции f(х)
в точке
».
Понятие односторонних пределов.
Формулировка теоремыo
существовании предела функции f(х)
в точке
 .
.
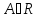 называется
предел функции f(x)
при
называется
предел функции f(x)
при
 ,
если для любого
,
если для любого ,
что при всех
,
что при всех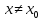 и
и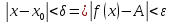
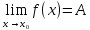
Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).
Для того чтобы функция f : E → R имела в точке x0 конечный предел, необходимо и достаточно, чтобы функция f удовлетворяла в точке x0 условию Коши.
Будем говорить, что функция f : E → R удовлетворяет в точке x0 (x0 — предельная точка множества E) условию Коши, если
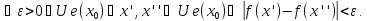
Определение предела функции на бесконечности.
 называется
предел функции f(x)
при
называется
предел функции f(x)
при
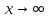 ,
если для любого
,
если для любого найдётся
найдётся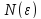 ,
что для всех
,
что для всех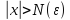 выполняется неравенство
выполняется неравенство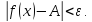
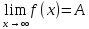
Теорема о сумме, разности, произведении и частном двух функций, имеющих пределы в точке.
Пусть функции f(x) и g(x) имеют пределы при одной и той же базе B:
![]()
Тогда функция h(x)=f(x)+g(x) также имеет предел при базе B, и этот предел L равен сумме пределов слагаемых:
![]()
Разность функций
![]()
Пусть функции f(x) и g(x) имеют пределы при одной и той же базе B:
![]()
Тогда функция h(x)=f(x) g(x) также имеет предел при базе B, и этот предел L равен произведению пределов сомножителей:
![]()
Пусть
при одной и той же базе B существуют
пределы ![]() и
и ![]() ,
причём
,
причём ![]() .
Тогда функция
.
Тогда функция 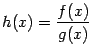 определена
на некотором окончании базы B,
существует предел
определена
на некотором окончании базы B,
существует предел ![]() ,
и
,
и  ,
то есть предел отношения равен отношению
пределов числителя и знаменателя.
,
то есть предел отношения равен отношению
пределов числителя и знаменателя.
Теорема о пределе функции, заключенной между двумя функциями, имеющими один и тот же предел.
Если функция f(x) заключена между двумя функциями g(x) и p(x), имеющими один и тот же предел, то она стремится к этому же пределу.
Определение бесконечно малой функции. Теорема о сумме и произведении конечного числа бесконечно малых функций, а также о произведении бесконечно малой функции на ограниченную функцию.
Функция
 называется бесконечно малой при
называется бесконечно малой при ,
если
,
если


Сумма и произведение конечного числа бесконечно малой функции есть функция бесконечно малая.
Произведение бесконечно малой функции на ограниченную есть функция бесконечно малая.
Теорема о необходимом и достаточном условиях выполнения равенства
 с
использованием понятия бесконечно
малой функции. Бесконечно большие
функциии
их свойства.
с
использованием понятия бесконечно
малой функции. Бесконечно большие
функциии
их свойства.
Если f(x) имеет предел, то её можно представить как сумму постоянной и бесконечно малой функции.

Функция
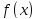 называется бесконечно большой при
называется бесконечно большой при ,
если
предел этой функции
,
если
предел этой функции
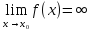
Сумма и произведение бесконечно больших функций есть функция бесконечно большая.
Сумма бесконечно большой функции и ограниченой есть функция бесконечно большая
Произведение
бесконечно большой функции на
 есть
функция бесконечно большая.
есть
функция бесконечно большая.
Правила сравнения бесконечно малых функций.
Допустим,
у нас есть бесконечно малые при одном
и том же ![]() величины
величины![]() и
и![]()
Если ![]() ,
то
,
то![]() —
бесконечно малаявысшего
порядка малости,
чем
—
бесконечно малаявысшего
порядка малости,
чем ![]() .
Обозначают
.
Обозначают![]() .
.
Если ![]() ,
то
,
то![]() —
бесконечно малаянизшего
порядка малости,
чем
—
бесконечно малаянизшего
порядка малости,
чем ![]() .
Соответственно
.
Соответственно![]() .
.
Если ![]() (предел
конечен и не равен 0), то
(предел
конечен и не равен 0), то![]() и
и![]() являются
бесконечно малыми величинамиодного
порядка малости.
являются
бесконечно малыми величинамиодного
порядка малости.
Это
обозначается как ![]() или
или![]() (в
силу симметричности данного отношения).
(в
силу симметричности данного отношения).
Если ![]() (предел
конечен и не равен 0), то бесконечно малая
величина
(предел
конечен и не равен 0), то бесконечно малая
величина![]() имеет
имеет![]() -й
порядок малости относительно
бесконечно малой
-й
порядок малости относительно
бесконечно малой ![]() .
.
Первый замечательный предел.
Предел
отношения sinx
к x
при
 равен
1.
равен
1.
![]()
Второй замечательный предел.
![]() или
или ![]()
Определения непрерывности функции.
Функция называется непрерывной на отрезке, если она непрерывна в каждой точке этого отрезка.
Точки разрыва функции и их классификация.
Точка
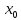 называетсяточкой
разрыва функции
f(x), если f(x) не определена в точке
называетсяточкой
разрыва функции
f(x), если f(x) не определена в точке
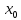 или не является непрерывной в этой
точке.
или не является непрерывной в этой
точке.
Точка
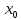 называется точкой разрыва1-го
рода,
если в этой точке функция f(x) имеет
конечные, но не равные друг другу левый
и правый пределы. (скачок)
называется точкой разрыва1-го
рода,
если в этой точке функция f(x) имеет
конечные, но не равные друг другу левый
и правый пределы. (скачок)
![]()
Точка
 называется точкой разрыва2–го
рода,
если в этой точке функция f(x) не имеет
хотя бы одного из односторонних пределов
или хотя бы один из них бесконечен.
называется точкой разрыва2–го
рода,
если в этой точке функция f(x) не имеет
хотя бы одного из односторонних пределов
или хотя бы один из них бесконечен.
