
Тема 2. Векторная алгебра
Основные понятия векторной алгебры. Линейные операции над векторами. Угол между векторами.
Вектор - это направленный отрезок, который имеет начало и конец.
Длиной
ненулевого вектора
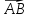 называется
длина отрезка AB.
называется
длина отрезка AB.
Нулевой вектор — вектор, начало которого совпадает с его концом.
Орты – единичный вектор.
Чтобы
сложить
два вектора, нужно от конца одного из
них отложить второй вектор; тогда сумма
– это вектор с началом в начале первого
вектора и концом в конце второго
вектора: 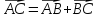 .
.
Разностью
двух векторов
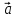 и
и  называется
такой третий вектор
называется
такой третий вектор 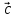 ,
который равен сумме векторов
,
который равен сумме векторов 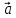 и
и 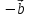 .
.
Угол между векторами — угол между направлениями этих векторов (наименьший угол).
Прямоугольная система координат. Координаты векторов. Разложение вектора по базису.
Прямоугольная система координат – система плоских координат образованная двумя взаимноперпендикулярными прямыми линиями, называемыми осями координат x и y. Точка их пересечения называется началом или нулем системы координат. Ось абсцисс – OX, ось ординат – OY.
Координаты вектора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
Разложение
вектора по базису имеет
вид:
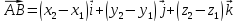
Направляющие косинусы векторов.
Направляющие косинусы вектора – это косинусы углов, которые вектор образует с положительными полуосями координат.
Чтобы найти направляющие косинусы вектора необходимо соответствующие координаты вектора поделить на модуль вектора.
Линейные операции над векторами в координатах. Условие коллинеарности векторов.
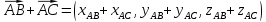
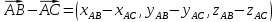
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
a={ax; ay; az} и b={bx; by; bz} коллинеарны если
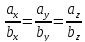
Скалярное произведение двух векторов. Условие ортогональности.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Свойства скалярного умножения. Скалярные произведения координатных ортов.
Свойства скалярного умножения:
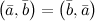 -
симметричность.
-
симметричность. .
Обозначается
.
Обозначается 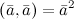 и
называется скалярный квадрат.
и
называется скалярный квадрат.Если
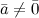 ,
то
,
то 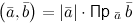
Если
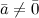 и
и 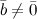 и
и 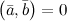 ,
то
,
то  .
Верно и обратное утверждение.
.
Верно и обратное утверждение.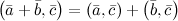
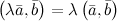
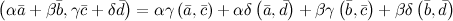
Скалярные произведения координатных ортов. i · j = j · i = 0, j · k = k · j = 0, k · i = i · k = 0.
Скалярное произведение в координатной форме. Угол между векторами. Условие перпендикулярности двух векторов.
Скалярное
произведение в координатной форме.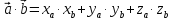
Угол
между векторами. ![]()
![]()
Для
перпендикулярности
двух ненулевых векторов
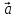 и
и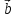 необходимо и достаточно, чтобы их
скалярное произведение равнялось нулю,
то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их
скалярное произведение равнялось нулю,
то есть, чтобы выполнялось равенство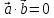 .
.
Необходимое
и достаточное условие
перпендикулярности двух векторов
в координатах имеет вид
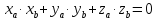 .
.
Проекция вектора на ось и на другой вектор.
Проекцией вектора 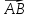 на
ось
l называется
длина его составляющей
на
ось
l называется
длина его составляющей 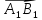 по
этой оси, взятая со знаком «+», если
по
этой оси, взятая со знаком «+», если 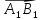 сонаправлен с l,
и со знаком «-»,если
сонаправлен с l,
и со знаком «-»,если 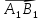 не
сонаправлен с l.
не
сонаправлен с l.
Проекцией вектора 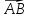 на
другой вектор
называется
длина его составляющей
на
другой вектор
называется
длина его составляющей 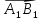 по
этому вектору, взятая со знаком «+»,
если
по
этому вектору, взятая со знаком «+»,
если 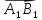 сонаправлен с этим вектором, и со знаком
«-»,если
сонаправлен с этим вектором, и со знаком
«-»,если 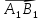 не
сонаправлен с ним
не
сонаправлен с ним
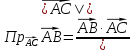 .
.
Векторное произведение двух векторов. Условие коллинеарности векторов. Вычисление площади параллелограмма и треугольника.
Векторным
произведением вектора 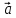 на
вектор
на
вектор 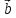 называется
третий вектор
называется
третий вектор 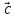 который
обладает следующими свойствами:
который
обладает следующими свойствами:
Его длина равна
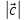 =
=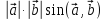
Вектор
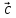 перпендикулярен
к плоскости, в которой лежат вектора
перпендикулярен
к плоскости, в которой лежат вектора 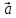 и
и 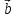
Вектор
 направлен
так, что поворот от вектора
направлен
так, что поворот от вектора 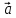 к
вектору
к
вектору 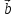 осуществляется
против часовой стрелки, если смотреть
из конца вектора
осуществляется
против часовой стрелки, если смотреть
из конца вектора 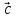 (в
этом случае, говорят, что тройка
векторов
(в
этом случае, говорят, что тройка
векторов 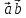 и
и 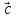 –
правая).
–
правая).
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
a={ax; ay; az} и b={bx; by; bz}
коллинеарны
если
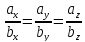
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма или удвоенной площади треугольника, построенных на этих векторах как на сторонах.
Свойства векторного умножения. Векторные произведения координатных ортов.
Основные свойства векторного произведения:
антикоммутативность:
![]() ;
;
однородность:
![]() ;
;
дистрибутивность:
![]() .
.
Векторное произведение ортов
i × j = k, j × i = − k , j × k = i, k × j = − i, k × i = j , i × k = − j .
Векторное произведение двух векторов в координатной форме.
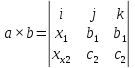
Смешанное произведение трех векторов. Условие компланарности векторов. Объём параллелепипеда и тетраэдра.
Смешанное произведение векторов a, b, c — скалярное произведение вектора a на векторное произведение векторов b и c.
Векторы называются компланарными, если существует плоскость, которой они параллельны.
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда или шести объёмам тетрайдера, образованных векторами a, b, c.
Смешанное произведение трех векторов в координатной форме. Свойства смешанного произведения.
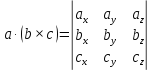
Свойства
перестановка любых двух сомножителей меняет знак произведения, т.е.: (a, b, c) = - (b, a, c) = (b, c, a) = - (c, b, a) = (c, a, b) = - (a, c, b)
если смешанное произведение равно нулю ((a, b, c) = 0), то векторы a, b, c - компланарны
