Тема 3. Элементы аналитической геометрии

1. Уравнение прямой на плоскости и в пространстве, заданной точкой и направляющим вектором. Параметрические уравнения прямой.

На плоскости 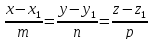; В пространстве

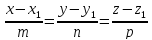
Параметрические уравнения прямой.

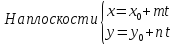
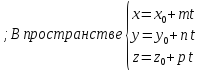
2. Уравнение прямой с угловым коэффициентом.

y = kx + b, где k - угловой коэффициент прямой, т. е. тангенс того угла, который прямая образует с положительным направлением оси Ox, причем этот угол отсчитывается от оси Ox к прямой против часовой стрелки, b - величина отрезка, отсекаемого прямой на оси ординат. При b = 0 уравнение имеет вид y = kx и соответствующая ему прямая проходит через начало координат.

3. Уравнение прямой на плоскости и в пространстве, проходящей через две данные точки.

На плоскости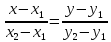В пространстве

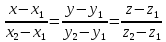
4. Общие уравнения прямой линии на плоскости и в пространстве.

На плоскости A₁ x + B₁ y + D₁ = 0, A₂ x + B₂ y + D₂ = 0; 

В пространстве A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0; 

5. Уравнение прямой на плоскости в «отрезках».

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: или

, где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

6. Нормальное уравнение прямой на плоскости.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим xcosφ + ysinφ - p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

7. Угол между двумя прямыми на плоскости и в пространстве. Условия перпендикулярности и коллинеарности прямых.

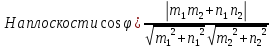
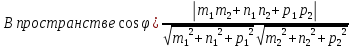
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны. 

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю (скалярное произведение).

8. Расстояние от точки до прямой.

Расстояние d от точки M₁(x₀;y₀) до прямой Ax + By + C = 0 вычисляется по формуле: 

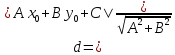
9. Общее уравнение плоскости.

Ax + By + Cz + D = 0

10. Уравнение плоскости, проходящей через три точки.

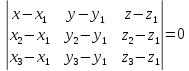
11. Уравнение плоскости в «отрезках».

 –плоскость, отсекающая от осей координат отрезки величиной а, b  и с соответственно, где обозначено.

12. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.

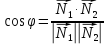
Две плоскости параллельны тогда и только тогда, когда их нормальные векторы параллельны, а значит .

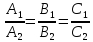Две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а значит .

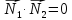13. Расстояние от точки до плоскости.

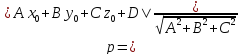
14. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.

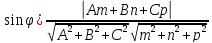
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

15. Кривые второго порядка (Эллипс, гипербола, парабола).

Эллипс — это линия, которая в некоторой прямоугольной декартовой системе координат Oxy координат имеет уравнение

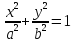
Фокальное свойство эллипса: Эллипс является множеством точек, сумма расстояний от которых до фокусов постоянна: F1M + F2M = 2a.

Директориальное свойство эллипса: Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно (и равно ε).

Гипербола — эта линия, которая в некоторой прямоугольной декартовой системе координат Oxy координат имеет уравнение

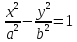
Фокальное свойство гиперболы: Гипербола является геометрическим местом точек, разность расстояний от которых до фокусов по абсолютной величине постоянна: |F1M − F2M| = 2a.

Директориальное свойство гиперболы: Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно (и равно ε).

Парабола — эта линия, которая в некоторой прямоугольной декартовой системе координат Oxy координат имеет уравнение

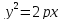
Теорема.

Парабола представляет собой множество точек, равноудаленных от данной прямой (директрисы параболы) и данной точки (фокуса параболы), не лежащей на директрисе.