
- •В.С. Васильева, с.В. Коровина, л.В. Марченко дискретная математика
- •Васильева, в.С.
- •Введение
- •1. Элементы теории множеств
- •1.1. Основные понятия теории множеств. Способы задания множеств
- •1.2. Операции над множествами
- •1.3. Диаграммы Эйлера – Венна
- •1.4. Свойства операций над множествами
- •1.5. Декартово произведение множеств
- •1.6. Бинарные отношения. Свойства бинарных отношений
- •1.7. Функция
- •2. Элементы математической логики
- •2.1. Математическая логика как наука
- •2.2. Высказывания. Логические операции и их основные свойства
- •Логические операции
- •Новые логические операции
- •2.3. Способы решения логических задач
- •2.4. Булевы функции. Свойства элементарных булевых функций
- •2.5. Дизъюнктивные и конъюнктивные нормальные формы булевых функций
- •2.6. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
- •3. Элементы теории графов
- •3.1. Основные понятия теории графов
- •3.2. Способы задания графов
- •3.3. Связность графов
- •4. Элементы комбинаторики
- •4.1. Перестановки, размещения и их количество
- •4.2. Сочетания и их свойства
- •4.3. Выборки с повторением
- •5. Индивидуальные задания
- •Заключение
- •Библиографический список
- •Оглавление
1.7. Функция
Отношения
эффективно применяются для описания
связей между парами элементов, выбранных
из двух множеств
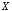 и
и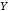 .
Функции – частный случай бинарных
отношений, на которые наложены
дополнительные ограничения.
.
Функции – частный случай бинарных
отношений, на которые наложены
дополнительные ограничения.
Рассмотрим
два произвольных множества
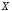 и
и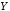 ,
элементы которых будем обозначать
,
элементы которых будем обозначать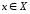 ,
,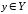 .
.
Определение
1.
поставим
каждому элементу
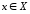 в соответствие один и только один элемент
в соответствие один и только один элемент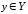 по определенному правилу
по определенному правилу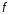 .
Тем самым зададимотображение
множества
.
Тем самым зададимотображение
множества
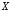 в множество
в множество .
Обозначение:
.
Обозначение: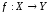 .
.
Часто вместо термина «отображение» используют термин «функция».
Пусть
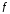 – функция из множества
– функция из множества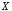 в множество
в множество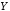 .
Поскольку для каждого
.
Поскольку для каждого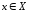 существует единственным образом
определенный
существует единственным образом
определенный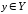 ,
такой, что
,
такой, что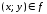 ,
то будем писать
,
то будем писать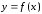 и говорить, что функция
и говорить, что функция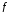 отображает множество
отображает множество в множество
в множество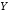 .
При этом элементы
.
При этом элементы
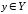 называютсяобразом
называютсяобразом
 при отображении
при отображении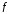 ,
а совокупность элементов
,
а совокупность элементов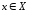 называетсяпрообразом
элемента
называетсяпрообразом
элемента
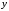 и обозначается
и обозначается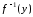 .
.
Множество
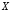 принято называтьобластью
определения функции.
Обозначение:
принято называтьобластью
определения функции.
Обозначение:
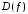 .
Множество
.
Множество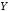 –областью
значений
функции
–областью
значений
функции
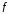 .
Обозначение:
.
Обозначение: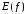 .
.
Способы задания функций:
аналитический (одной или совокупностью формул);
табличный;
описательный;
графический.
Определение
2. Графиком
функции
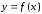 является изображение в декартовой
системе координат множества точек
является изображение в декартовой
системе координат множества точек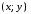 ,
где
,
где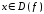 ,
а
,
а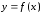 ,
т. е. изображение декартова произведения
области определения функции и области
ее значений.
,
т. е. изображение декартова произведения
области определения функции и области
ее значений.
Например,
график
функции
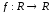 ,
заданный формулой
,
заданный формулой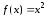 ,
изображен на рис. 11.
,
изображен на рис. 11.
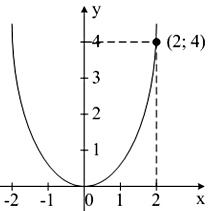
Рис. 11
Множество
определения – ось
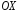 –
множество действительных чисел, множество
значений – ось
–
множество действительных чисел, множество
значений – ось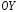 – множество неотрицательных действительных
чисел.
– множество неотрицательных действительных
чисел.
График
функции состоит из точек
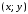 прямого произведения
прямого произведения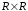 ,
для которых
,
для которых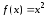 .
.
Пример
1.
Найдите область определения функции
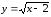 .
.
Решение
Функция
содержит корень четной степени,
следовательно, она определена только
в случае неотрицательного подкоренного
выражения, т. е.
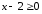 ,
откуда
,
откуда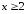 ;
;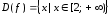 .
.
Пример
2.
Найдите прообраз множества
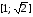 при отображении
при отображении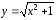 .
.
Решение
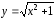
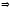
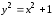
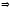
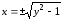 .
.
Подставим
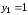 ,
получим
,
получим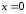 ;
;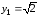 ,
получим
,
получим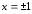 .
.
Прообразом
отображения (в силу непрерывности
функции) являются те
 ,
которые попадают в отрезок
,
которые попадают в отрезок
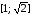 ,
тогда
,
тогда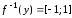 .
.
Пример
3.
Отображение
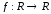 действует по правилу
действует по правилу
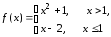 .
Найдите образ
.
Найдите образ
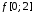 .
.
Решение
Отрезок
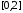 можно представить как объединение двух
множеств:
можно представить как объединение двух
множеств: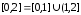 .
Отрезок
.
Отрезок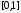 отображается аналитическим выражением
отображается аналитическим выражением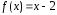 ,
поэтому
,
поэтому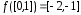 .
Полуинтервал
.
Полуинтервал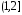 отображается аналитическим выражением
отображается аналитическим выражением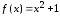 ,
поэтому
,
поэтому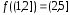 .
Окончательно образ имеет следующий вид
.
Окончательно образ имеет следующий вид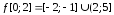 .
.
Вопросы и задачи для самостоятельного решения
1. Дайте определения образа, прообраза функции.
2.
Найдите прообраз множества
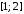 при отображении
при отображении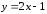 .
.
3.
Отображение
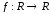 действует по правилу
действует по правилу
 .
Найдите образ
.
Найдите образ
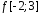 .
.
4. Найдите области определения следующих функций:
а)
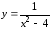 ;
б)
;
б)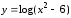 .
.
2. Элементы математической логики
2.1. Математическая логика как наука
Как самостоятельная наука логика оформилась в трудах греческого философа Аристотеля (384–322 гг. до н.э.). Он систематизировал известные до него сведения, и эта система стала впоследствии называться формальной, или аристотелевой, логикой. Формальная логика просуществовала без серьезных изменений более двадцати столетий. Сочинение Аристотеля «Аналитики» долгое время рассматривали как труд, завершающий развитие этой науки. Исследования математики выявили недостаточность аристотелевой логики и потребовали дальнейшего ее развития.
Логика – это наука о рассуждениях, которая позволяет определить истинность или ложность того или иного математического утверждения, исходя из совокупности первичных предположений, называемых аксиомами.
Впервые в истории идеи о построении логики на математической основе были высказаны немецким математиком Г. Лейбницем (1646–1716) в конце XVII в. Он считал, что основные понятия логики должны быть обозначены символами, которые соединяются по особым правилам.
Первая
реализация идеи Г. Лейбница принадлежит
английскому ученому Дж. Булю
(1815–1864).
Он
создал алгебру, в которой буквами
обозначались высказывания, что привело
к появлению алгебры высказываний. Именно
благодаря введению символов в логику
была получена основа для создания новой
науки – математической логики. Джордж
Буль развил алгебраический подход к
логике и сформулировал правила логических
вычислений. В труде «Исследование
законов мышления» он использовал
алгебраическую символику для логических
операций. Так, операция отрицания
переменной
 вычислялась как разность
вычислялась как разность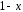 ,
дизъюнкция (логическое сложение)
переменных
,
дизъюнкция (логическое сложение)
переменных и
и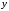 – как выражение
– как выражение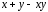 и т. д.
и т. д.
Современное обозначение логических операций, сходных с обозначениями теоретико-множественных операций, ввел русский математик П.С. Порецкий (1846–1907).
К концу XIX столетия актуальное значение для математики приобрели вопросы обоснования ее понятий и идей. Эти задачи имели логическую природу и, естественно, привели к дальнейшему развитию математической логики. В этом отношении показательны работы немецкого математика Г. Пеано (1858–1925), который применил математическую логику для обоснования арифметики и теории множеств.
Математическая (формальная) логика делится на три подраздела: логику Буля, логику высказываний и логику предикатов.
Основным объектом изучения в математической логике являются различные исчисления, например исчисление высказываний, исчисление предикатов. Основным предметом алгебры логики являются высказывания и логические операции над ними. Суть формального рассуждения – одна из основных тем формальной логики, широко применяемая при изучении математических доказательств.
Математическая логика играет большую роль в математике, так как при систематическом изложении математики возникает проблема выбора исходных понятий и правил, которые представляют базис всего изложения.
